Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численные методы
Содержание
- 1. Численные методы
- 2. Турчак Л.Е. Основы численных методов. Учебное пособие.
- 3. Область применения численных методов – решение тех
- 4. АналитическиеТеоретические рассуждения и выводы. Рассматриваются в курсе
- 5. ГрафическиеПостроение графиков, диаграмм, запись измерений с помощью
- 6. ЧисленныеРешение задачи сводится к вычислению в определенной
- 7. Численные методы позволяют свести решение задачи к
- 8. 1. Вычисления с помощью ручки и бумаги
- 9. Постановка задачи (исходные данные и определение конечного
- 10. Опр. Нелинейным называется уравнение, которое содержит неизвестное
- 11. 1. Локализация корня X0, т.е. нахождение интервала
- 12. Постановка задачи: Решить уравнение f(x)=0.Пусть на интервале
- 13. Тогда, чтобы найти корень уравнения X0 необходимо
- 14. 5. Переопределить интервал: новый интервал поиска снова
- 15. Слайд 15
- 16. 1. Локализация корня. Составим таблицу значений функции
- 17. 1 итерация a:= 1
- 18. 1. Метод бисекции (деление отрезка пополам);2. Метод хорд (метод касательных);3. Метод итераций (метод последовательных приближений).
- 19. Постановка задачи та же, что и в
- 20. Неподвижна та граница интервала, для которой знак
- 21. Из подобия треугольников ΔAax1 и ΔABC следует:
- 22. Найдем значение в т. x1:Тогда последовательно находим следующие точки:и т.д. Окончательно получаем:(*)
- 23. НЕПОДВИЖНА ТОЧКА А.Проводим хорду AB, которая делит
- 24. Из подобия треугольников ΔBbx1 и ΔABC следует:
- 25. Найдем значение в т. x1:Тогда последовательно находим следующие точки:и т.д. Окончательно получаем:(**)
- 26. Метод хорд заключается в том, что на
- 27. В матричном виде система уравнений записывается в
- 28. 1. Метод Крамера (Правило Крамера)2. Метод Гаусса
- 29. Скачать презентанцию
Турчак Л.Е. Основы численных методов. Учебное пособие. – М.:Наука. – 2003. – 320 с.Тарасевич. Основы численных методов на MathCADwww.exponenta.ruМудров А.Е. Числ. методы для ПЭВМ на языках Бэйсик, Фортран и Паскаль. –
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
Слайды и текст этой презентации
Слайд 2Турчак Л.Е. Основы численных методов. Учебное пособие. – М.:Наука. –
2003. – 320 с.
Числ. методы для ПЭВМ на языках Бэйсик, Фортран и Паскаль. – Томск:МП «Раско», 1991.
Слайд 3Область применения численных методов – решение тех задач математического анализа,
для которых аналитическое (точное) решение затруднено или невозможно
Примеры:
«неберущиеся» интегралы
(нет первообразных функций);Математические задачи, требующие больших затрат времени
и другие
Слайд 4Аналитические
Теоретические рассуждения и выводы. Рассматриваются в курсе математики, физики и
др. наук.
Конечный результат: Формулы, системы уравнений.
Преимущества:
Вычисления по конечным формулам,
Можно
строить графикиРешить доп. теоретические задачи
Недостатки:
Приближения при выводе формул
Отсутствие методов решения систем уравнений некоторого вида
Трудности проведения вычислений по формулам
Слайд 5Графические
Построение графиков, диаграмм, запись измерений с помощью датчиков.
Конечный результат: Графики
и точки на графиках.
Преимущества:
Наглядное представление о поведении исследуемой величины
Позволяет
оценить приближенное значение некоторой величиныМожно составить таблицу значений
Недостатки:
Трудности проведения дополнительных теоретических исследований
Слайд 6Численные
Решение задачи сводится к вычислению в определенной последовательности.
Конечный результат: Число
или числа.
Преимущества:
Решение задач, для которых нет аналитических методов
Недостатки:
Вычисления содержат
погрешностиНе для всех задач есть численные методы
Вычисления могут занимать много времени
Слайд 7Численные методы позволяют свести решение задачи к выполнению конечного числа
арифметических действий над числами, при этом результаты получаются в виде
числовых значений
Слайд 81. Вычисления с помощью ручки и бумаги можно проводить с
любой степенью точности
2. В компьютере числа хранятся в ячейках памяти
с фиксированной разрядностью не более 15 цифр. Ограничен диапазон представления чисел: 10-307 < |x| < 103073. Компьютерные вычисления могут содержать миллионы операций, что приводит к накоплению ошибки.
4. Компьютерная арифметика связана с представлением чисел в ЭВМ и отличается от обычной
Слайд 9Постановка задачи (исходные данные и определение конечного результата исследования).
Построение модели
(модель должна адекватно описывать законы физического явления).
Разработка численного метода (нахождение
метода, позволяющего свести задачу к вычислительному алгоритму).Все численные методы являются ПРИБЛИЖЕННЫМИ, т.е. решение всегда находится с некоторой погрешностью ε
Слайд 10Опр. Нелинейным называется уравнение, которое содержит неизвестное Xn (n≠1) или
переменная X входит под знак функции.
Опр. Уравнение называется трансцендентным, если
переменная X входит под знак какой-либо математической функции: корень, экспонента, тригонометрическая функция и др.Опр. Если в уравнении переменная X входит только в виде Xn (n≠1), то такое уравнение называется алгебраическим.
Слайд 111. Локализация корня X0, т.е. нахождение интервала (a,b), где X0∈(a,b),
в котором содержится корень уравнения.
2. Уточнение значения корня X0 до
заданной точности ε.а) Графически (строится приближенный график функции y=f(x))
б) Аналитически (строится таблица значений функции f(x)=0)
Слайд 12Постановка задачи: Решить уравнение f(x)=0.
Пусть на интервале [a,b] содержится один
корень уравнения x0. На данном интервале выполняются ограничения применимости метода:
f(a)
· f(b) ≤ 02. Существует f’(x) и не меняет знак на [a,b]
3. Функция f(x) непрерывна и дифференцируема на [a,b]
4. Задана точность нахождения корня X0: ε=10-3
![Постановка задачи: Решить уравнение f(x)=0.Пусть на интервале [a,b] содержится один корень уравнения x0. На данном интервале выполняются](/img/thumbs/458e890d1b1875d4f80c4f9a1e9996b6-800x.jpg "Численные методы Постановка задачи: Решить уравнение f(x)=0.Пусть на интервале [a,b] содержится один корень")
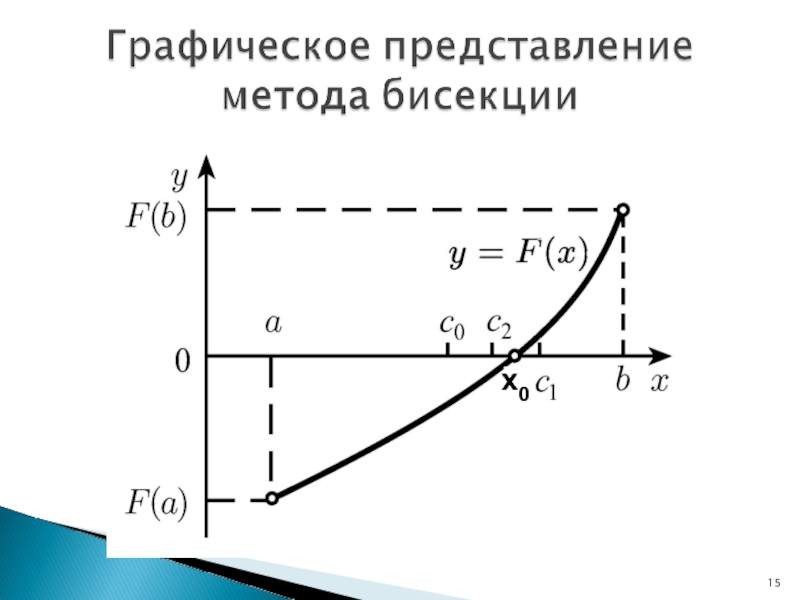
Слайд 13Тогда, чтобы найти корень уравнения X0 необходимо сделать следующее:
1. Найти
середину отрезка [a,b], точку c=(a+b)/2.
2. Найти значение функции f(x) в
точке с.3. Проверить, выполняется ли условие
f(с) · f(b) ≤ 0 (1).
4. В случае выполнения условия (1), сузить интервал поиска до [c,b]. Если условие (1) не выполняется – сузить интервал поиска до [a,c].
![Тогда, чтобы найти корень уравнения X0 необходимо сделать следующее:1. Найти середину отрезка [a,b], точку c=(a+b)/2.2. Найти значение](/img/thumbs/4c9279f00fc082b85fa84ad9c5867392-800x.jpg "Численные методы Тогда, чтобы найти корень уравнения X0 необходимо сделать следующее:1. Найти середину")
Слайд 145. Переопределить интервал: новый интервал поиска снова назвать как [a,b].
6.
Проверить, достигнута ли заданная точность ε:
| b – a| < ε7. Если точность достигнута, то вывести на печать значение корня X0 = (a+b)/2. Если точность не достигнута, то перейти к п 1. (к следующей итерации).
![5. Переопределить интервал: новый интервал поиска снова назвать как [a,b].6. Проверить, достигнута ли заданная точность ε:](/img/thumbs/140a5ac7af19171c713cb242086a344a-800x.jpg "Численные методы 5. Переопределить интервал: новый интервал поиска снова назвать как [a,b].6. Проверить,")
Слайд 161. Локализация корня. Составим таблицу значений функции f(x)=-x4+5:
Из таблицы видно,
что корень находится на интервале x ∈ [1,2].
Слайд 171 итерация
a:= 1 b:= 2
c:=(a+b)/2
c=1.5 f(b)*f(c) = 0.688 > 0
поэтому
b:=c|b-a|=0.5 > ε
2 итерация
c:=(a+b)/2 c=1.25 f(b)*f(c) = -0.16 < 0
поэтому a:=c
|b-a|=0.25 > ε
и т.д.
Слайд 181. Метод бисекции (деление отрезка пополам);
2. Метод хорд (метод касательных);
3.
Метод итераций (метод последовательных приближений).
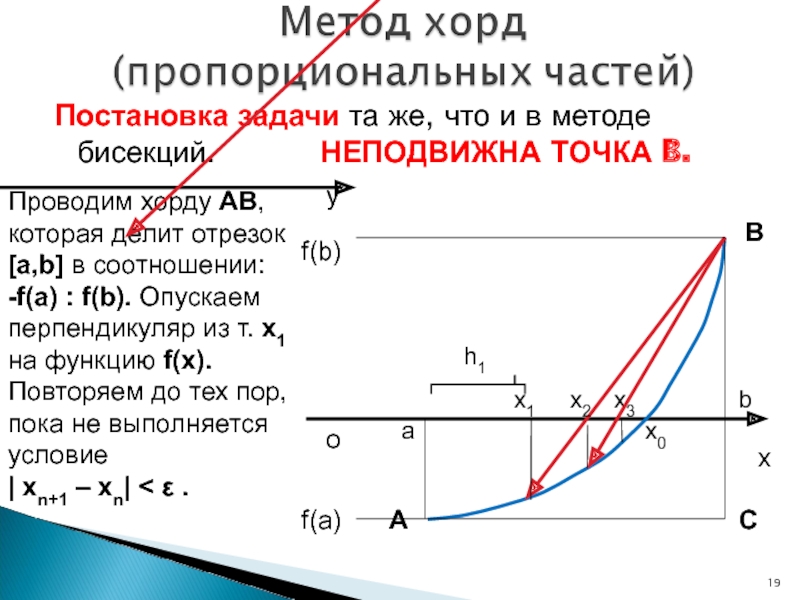
Слайд 19Постановка задачи та же, что и в методе бисекций.
НЕПОДВИЖНА ТОЧКА B.
Проводим хорду AB, которая
делит отрезок [a,b] в соотношении:-f(a) : f(b). Опускаем перпендикуляр из т. x1 на функцию f(x). Повторяем до тех пор, пока не выполняется условие
| xn+1 – xn| < ε .
Слайд 20Неподвижна та граница интервала, для которой знак функции f(x) совпадает
со знаком ее второй производной f ”(x), т.е. f(b)*f ”(b)
>0.Последовательные приближения xn лежат по ту сторону корня x0, где функция имеет знак, противоположный знаку ее второй производной.
Слайд 21Из подобия треугольников ΔAax1 и ΔABC следует:
Тогда длина отрезка
h1 равна:
?
Случай используется, если первая и вторая производные функции f(x)
имеют одинаковые знаки, т.е.f ‘(x)*f “(x) > 0
Слайд 22
Найдем значение в т. x1:
Тогда последовательно находим следующие точки:
и т.д.
Окончательно получаем:
(*)
Слайд 23НЕПОДВИЖНА ТОЧКА А.
Проводим хорду AB, которая делит отрезок [a,b] в
соотношении:
f(b) : -f(a). Опускаем перпендикуляр из т. x1 на функцию
f(x). Повторяем до тех пор, пока не выполняется условие | xn+1 – xn| < ε .
![НЕПОДВИЖНА ТОЧКА А.Проводим хорду AB, которая делит отрезок [a,b] в соотношении:f(b) : -f(a). Опускаем перпендикуляр из т.](/img/thumbs/84b2c65ff89e432a3d2b18fa71a7575b-800x.jpg "Численные методы НЕПОДВИЖНА ТОЧКА А.Проводим хорду AB, которая делит отрезок [a,b] в соотношении:f(b)")
Слайд 24Из подобия треугольников ΔBbx1 и ΔABC следует:
Тогда длина отрезка
h1 равна:
?
Случай используется, если первая и вторая производные функции f(x)
имеют разные знаки, т.е.f ‘(x)*f “(x) < 0
Слайд 25
Найдем значение в т. x1:
Тогда последовательно находим следующие точки:
и т.д.
Окончательно получаем:
(**)
Слайд 26Метод хорд заключается в том, что на отрезке [a,b] функция
f(x) заменяется стягивающей её хордой.
В качестве приближенного значения корня
x0 принимается точка пересечения хорды с осью Ox.![Метод хорд заключается в том, что на отрезке [a,b] функция f(x) заменяется стягивающей её хордой. В качестве](/img/thumbs/bb212cb3257709a1c7d1916802e3ce65-800x.jpg "Численные методы Метод хорд заключается в том, что на отрезке [a,b] функция f(x)")
Слайд 27В матричном виде система уравнений записывается в виде:
Здесь aij –
матрица коэффициентов при неизвестных;
Bj – вектор-столбец свободных членов;
Xj – вектор-столбец
неизвестных.Решение: Любая совокупность чисел α1, α2, …, αn, приводящая систему в тождество
Слайд 281. Метод Крамера (Правило Крамера)
2. Метод Гаусса (приведение расширенной матрицы
системы к треугольному виду):
а) неравенство нулю
диагонального элемента;б) с выбором главного элемента;
в) итерационный.
3. Метод Жордана-Гаусса.
