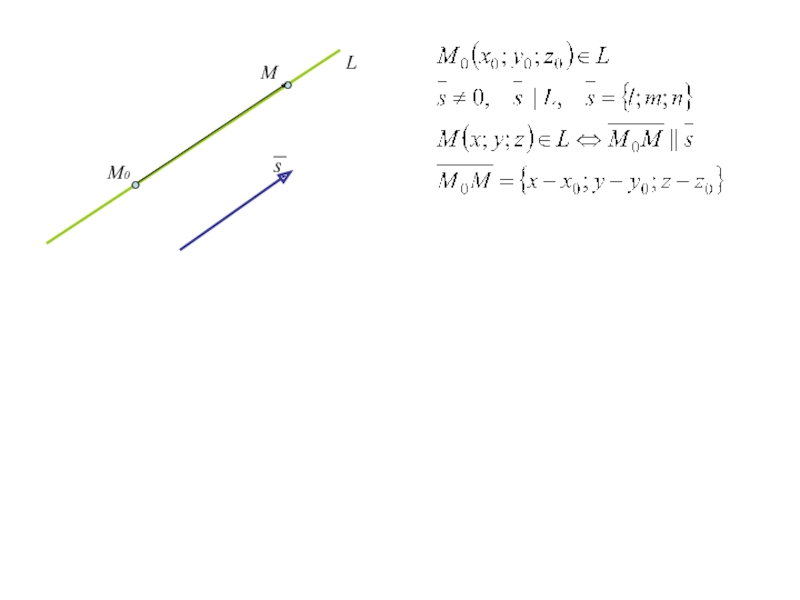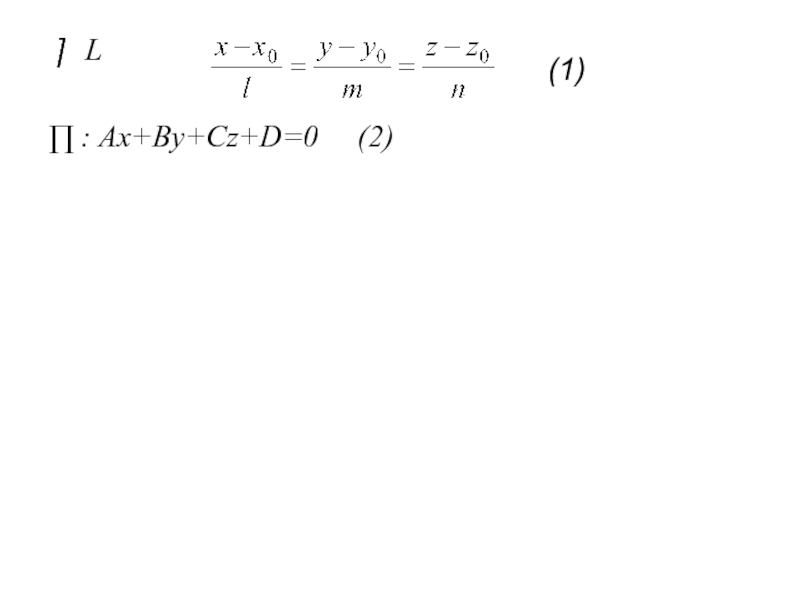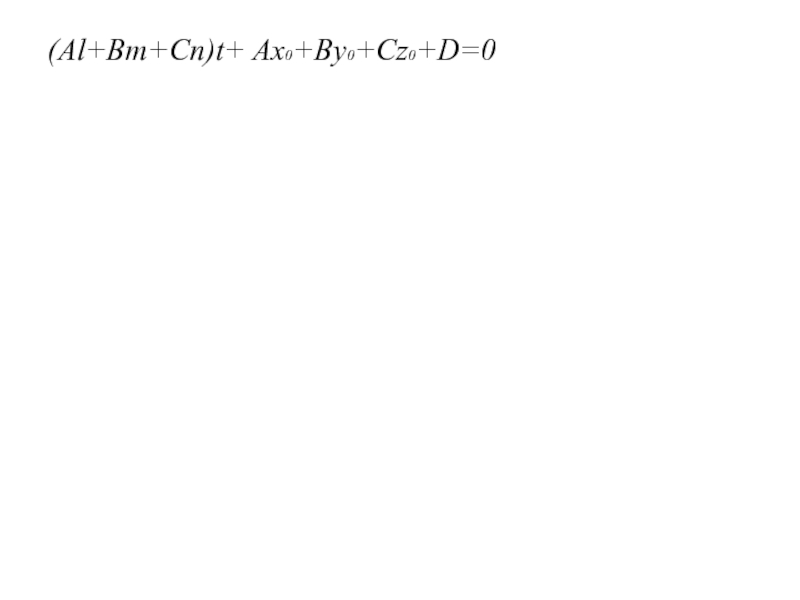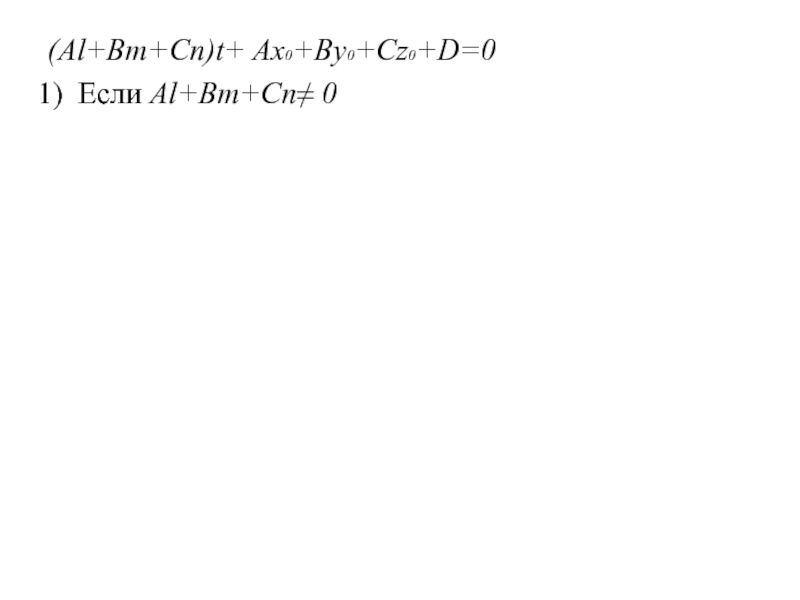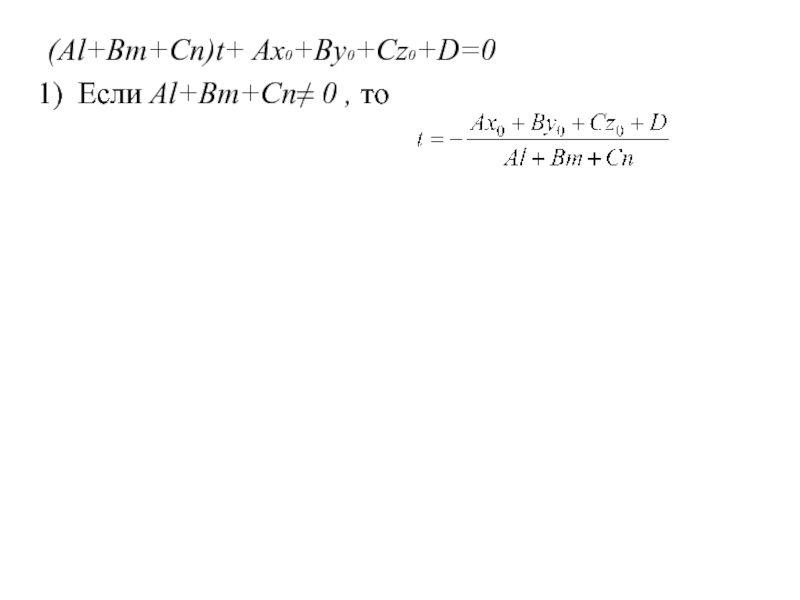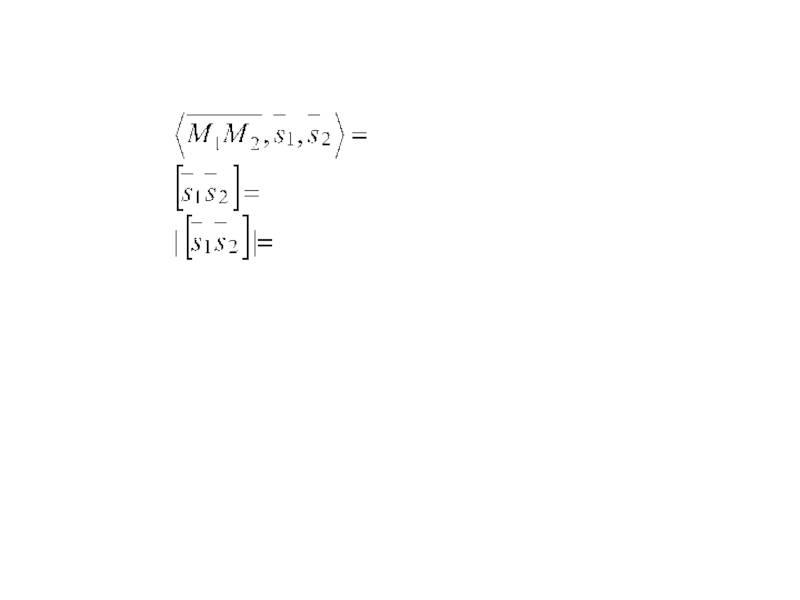Слайд 2Содержание
5. Уравнение прямой в пространстве
6. Уравнение прямой, проходящей через две
точки
7. Прямая как линия пересечения двух плоскостей
8. Параллельность прямой плоскости
9.
Угол между двумя прямыми. Условие параллельности и пер...
10. Условие принадлежности двух прямых к одной плоскости
11. Геометрический смысл неравенства первой степени с тр...
12. Расстояние от точки до плоскости
13. Расстояние от точки до прямой в пространстве
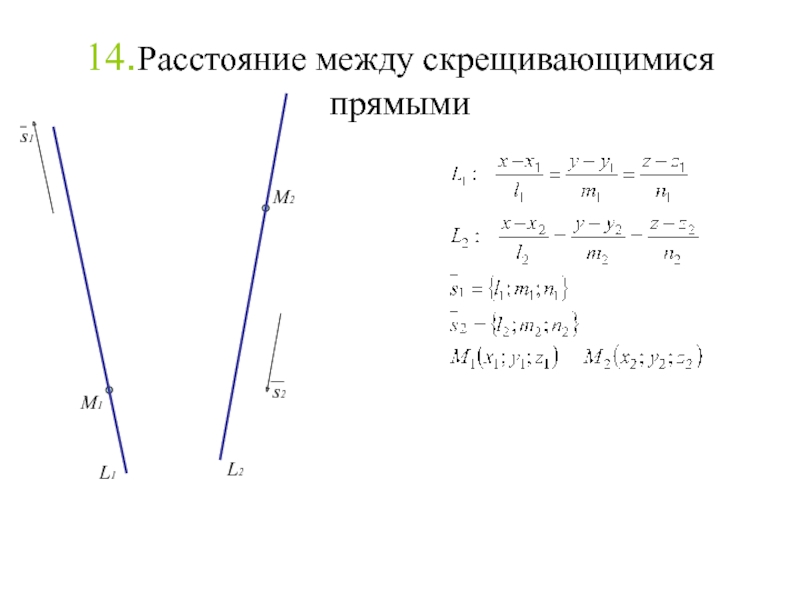
14.Расстояние между скрещивающимися прямыми
15. Угол между прямой и плоскостью
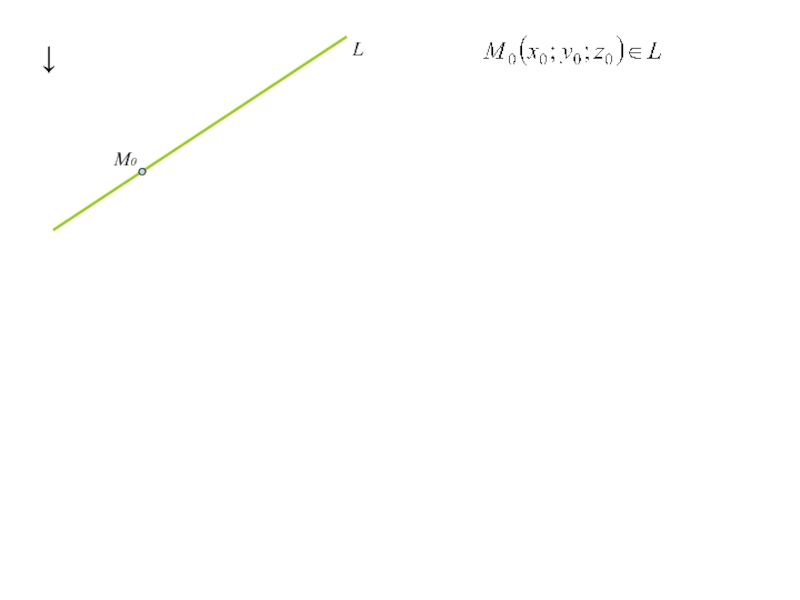
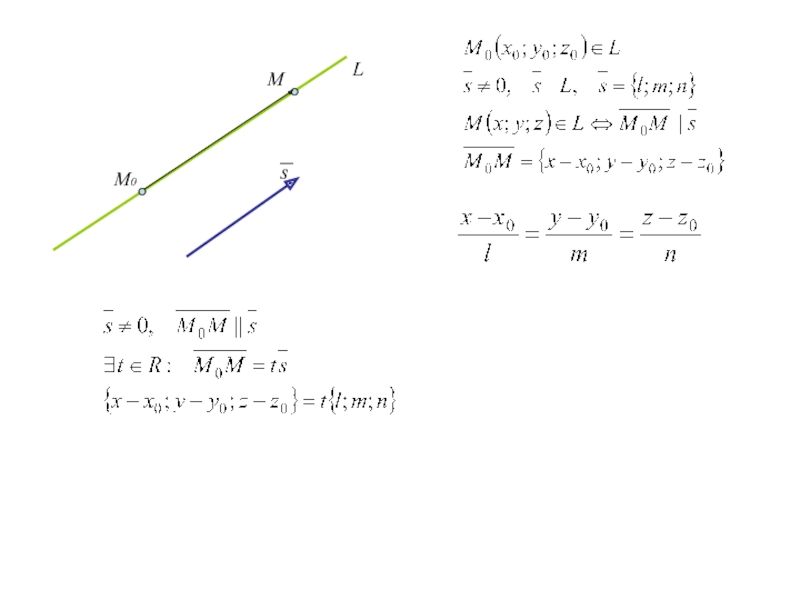
Слайд 35. Уравнение прямой в пространстве
Слайд 45. Уравнение прямой в пространстве
В ДПСК уравнения прямой, проходящей через
точку М0 (x0;y0;z0) и имеющей направляющий вектор s={l;m;n} имеют вид
(1)
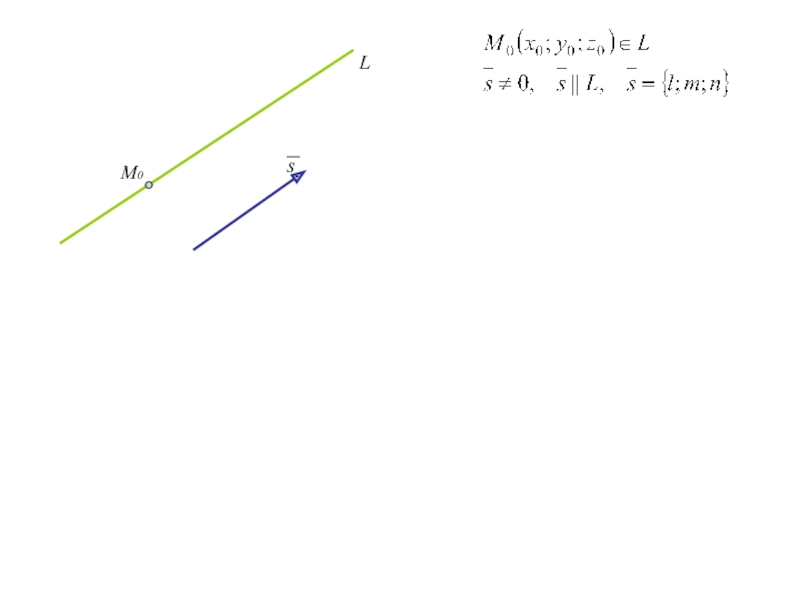
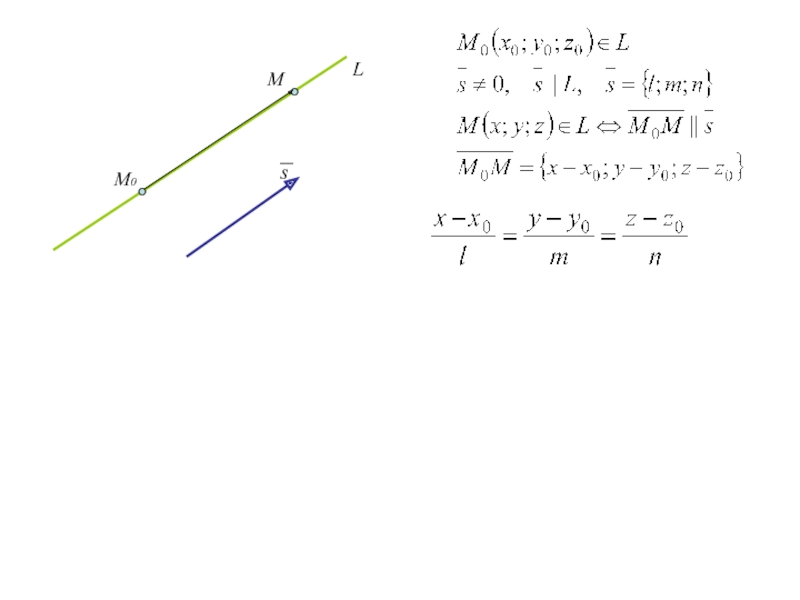
Слайд 55. Уравнение прямой в пространстве
В ДСК уравнения прямой, проходящей через
точку М0 (x0;y0;z0) и имеющей направляющий вектор s={l;m;n} имеют вид
(1)
(канонические уравнения прямой)
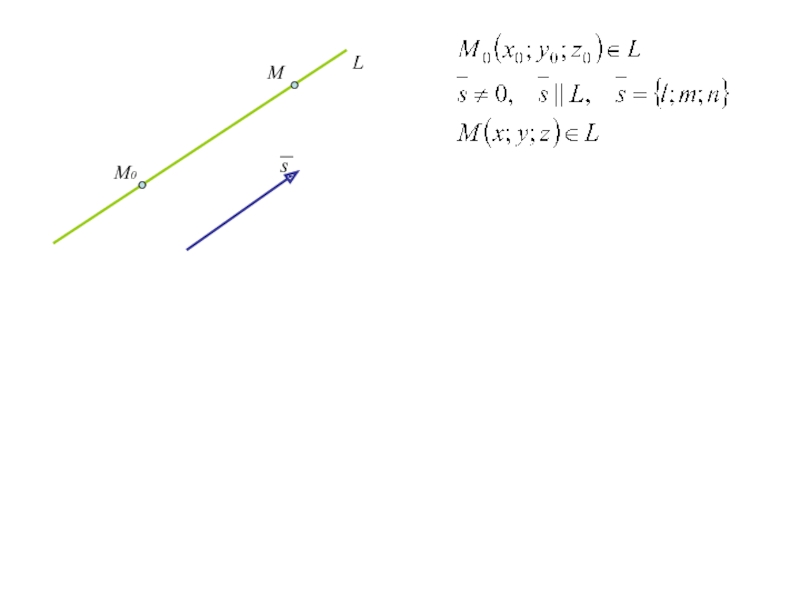
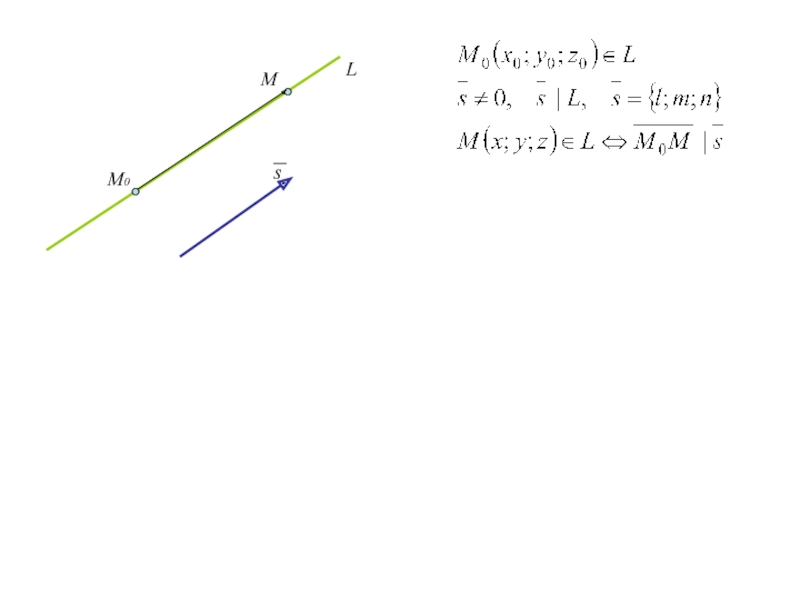
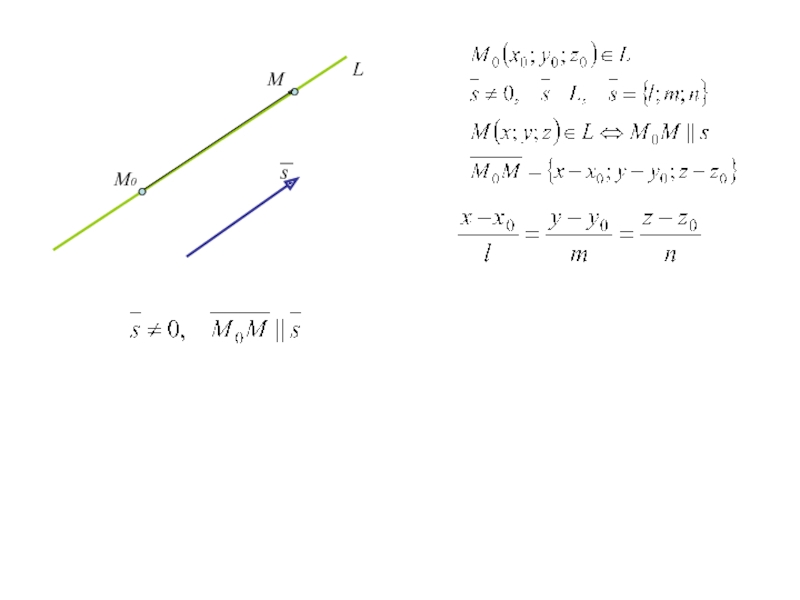
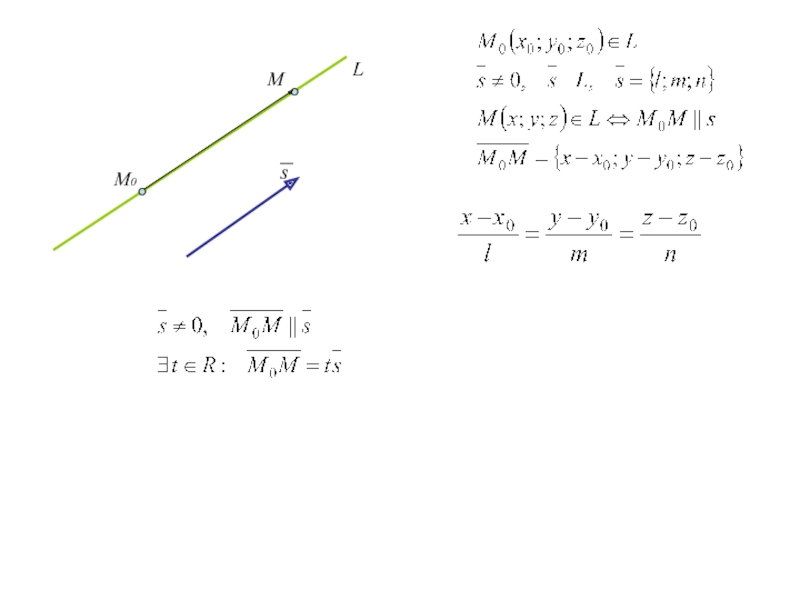
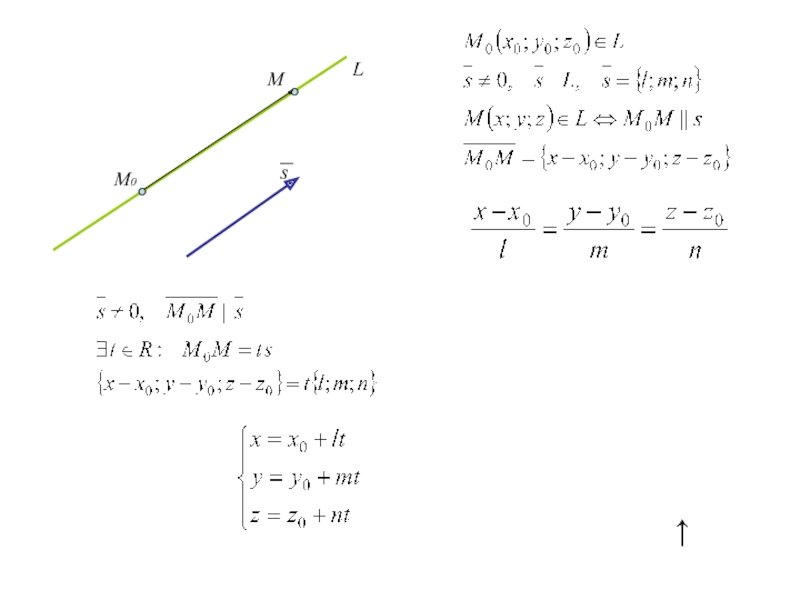
Слайд 65. Уравнение прямой в пространстве
В ДСК уравнения прямой, проходящей через
точку М0 (x0;y0;z0) и имеющей направляющий вектор s={l;m;n} имеют вид
(1)
(канонические уравнения прямой)
В параметрической форме
(2)
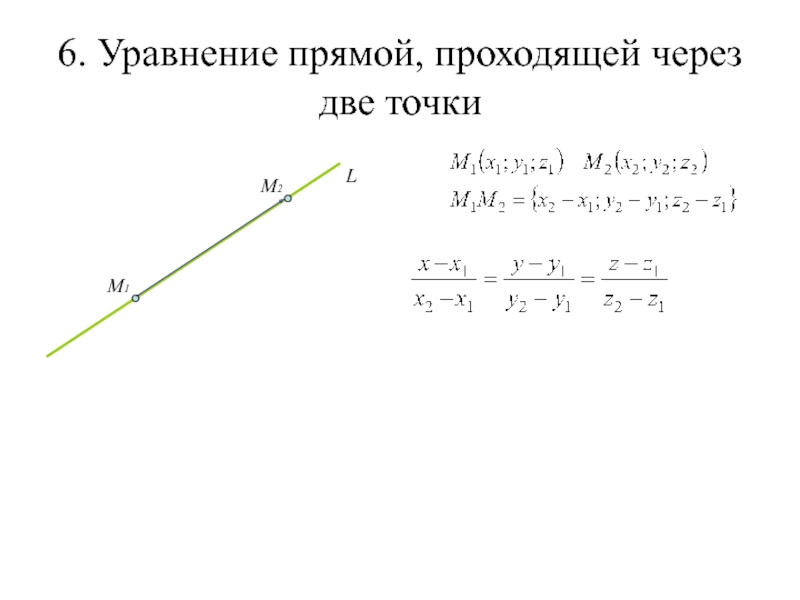
Слайд 186. Уравнение прямой, проходящей через две точки
Слайд 196. Уравнение прямой, проходящей через две точки
Слайд 206. Уравнение прямой, проходящей через две точки
M1
M2
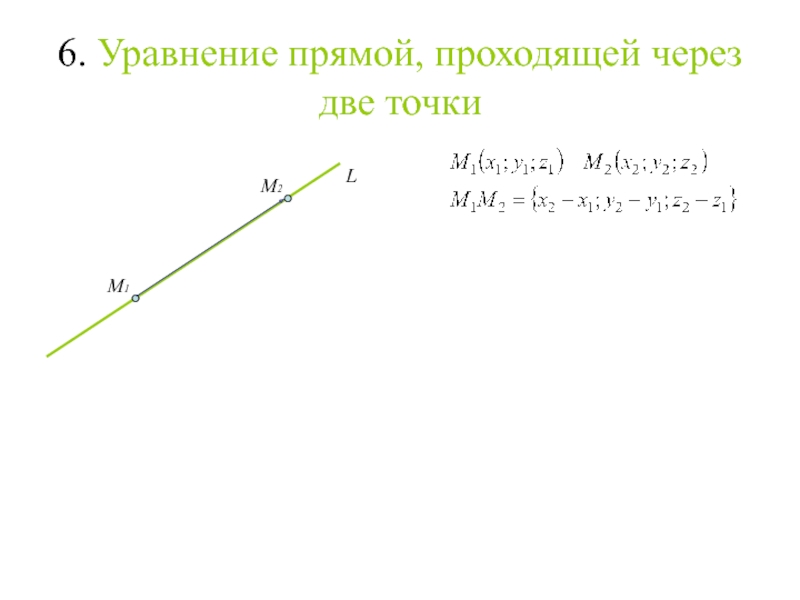
Слайд 216. Уравнение прямой, проходящей через две точки
L
M1
M2
Слайд 226. Уравнение прямой, проходящей через две точки
L
M1
M2
Слайд 236. Уравнение прямой, проходящей через две точки
L
M1
M2
Слайд 246. Уравнение прямой, проходящей через две точки
L
M1
M2
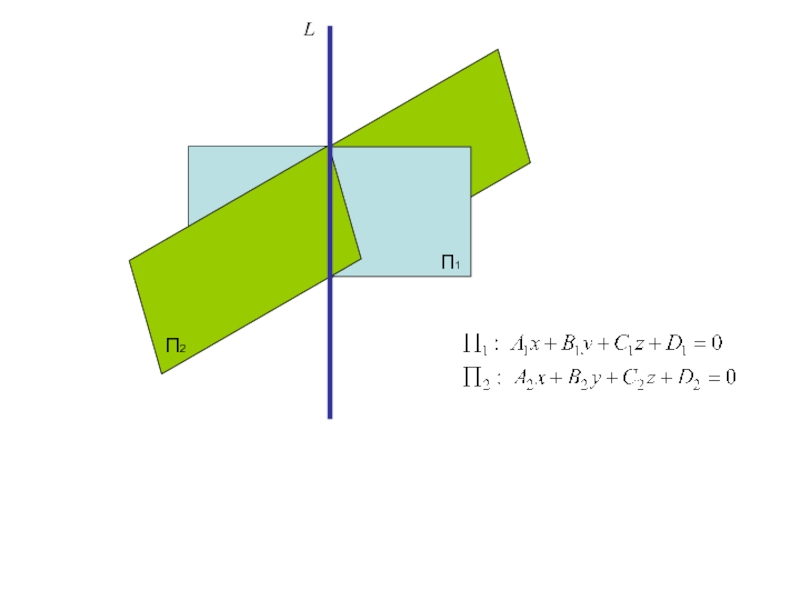
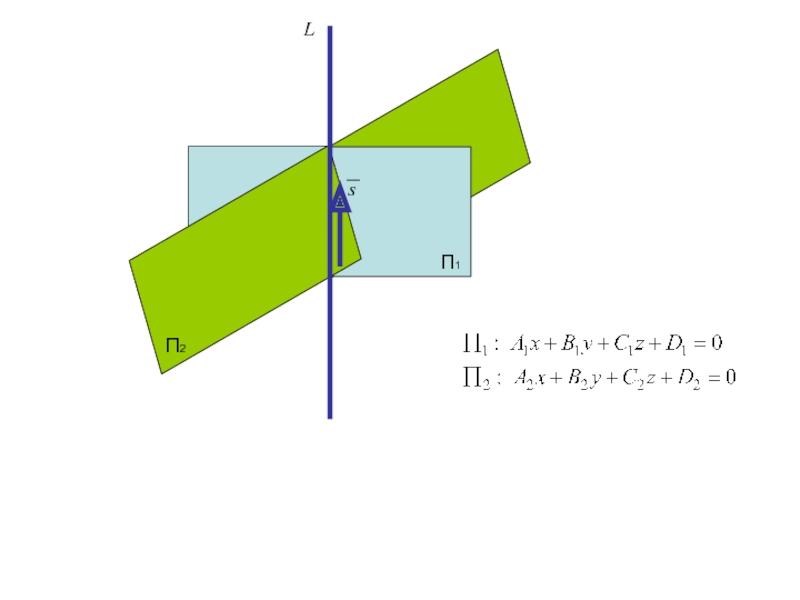
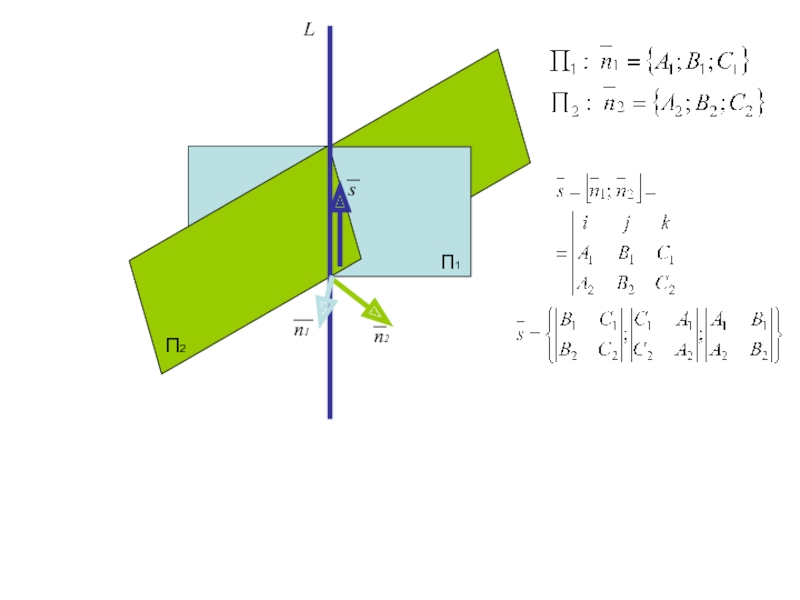
Слайд 257. Прямая как линия пересечения двух плоскостей
Слайд 31
Прямую L можно задать уравнениями двух плоскостей
П1
П2
L
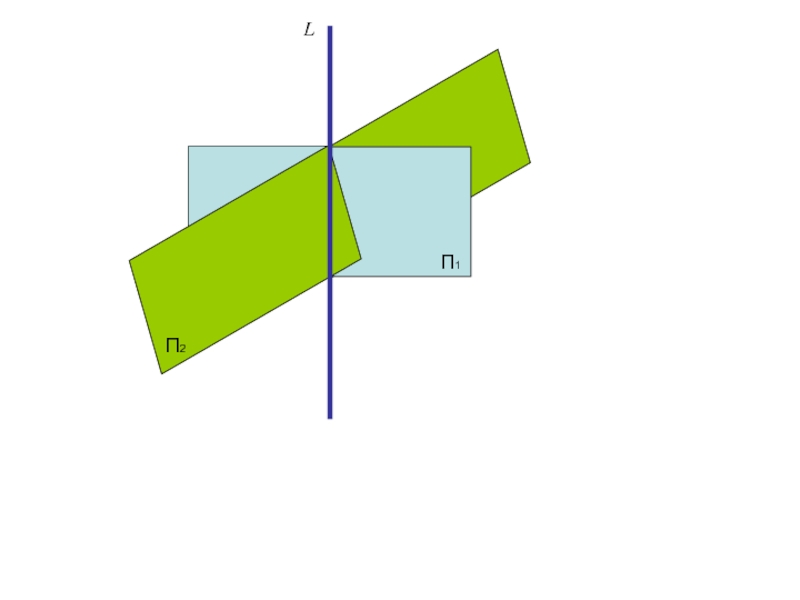
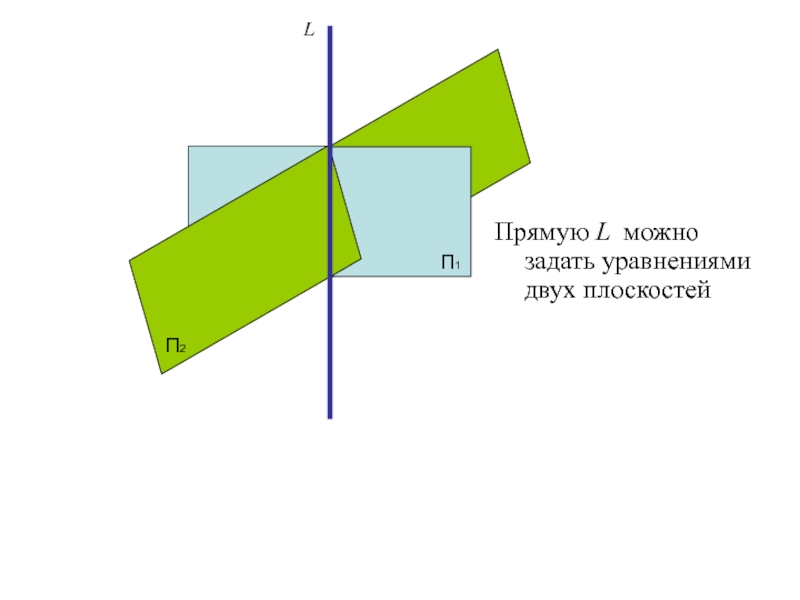
Слайд 32
Прямую L можно задать уравнениями двух плоскостей
П1
П2
L
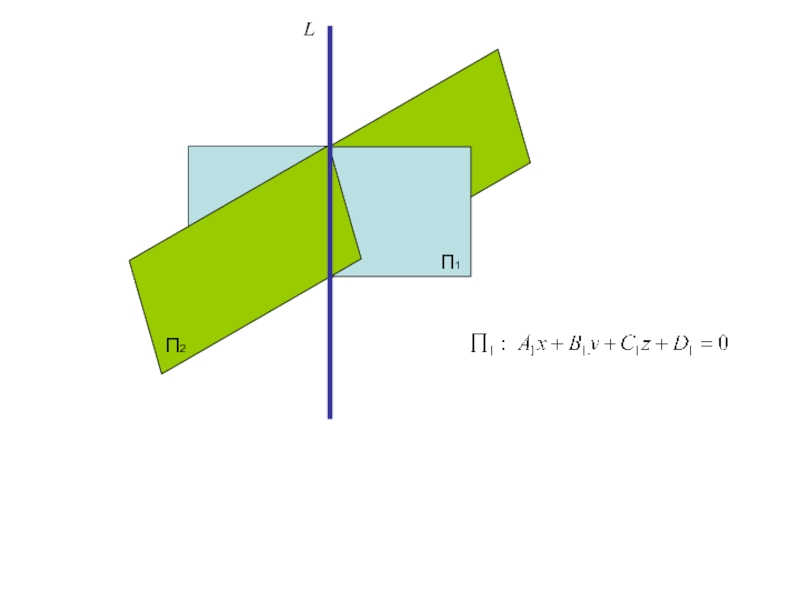
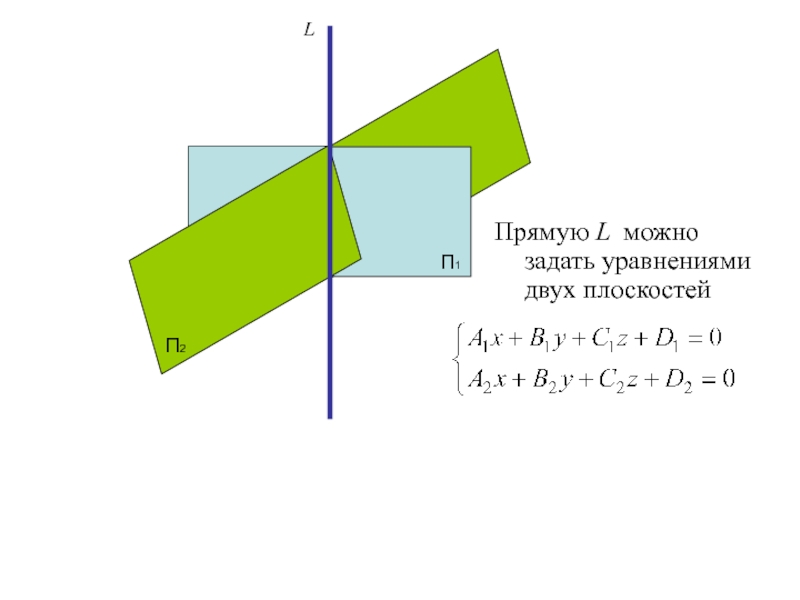
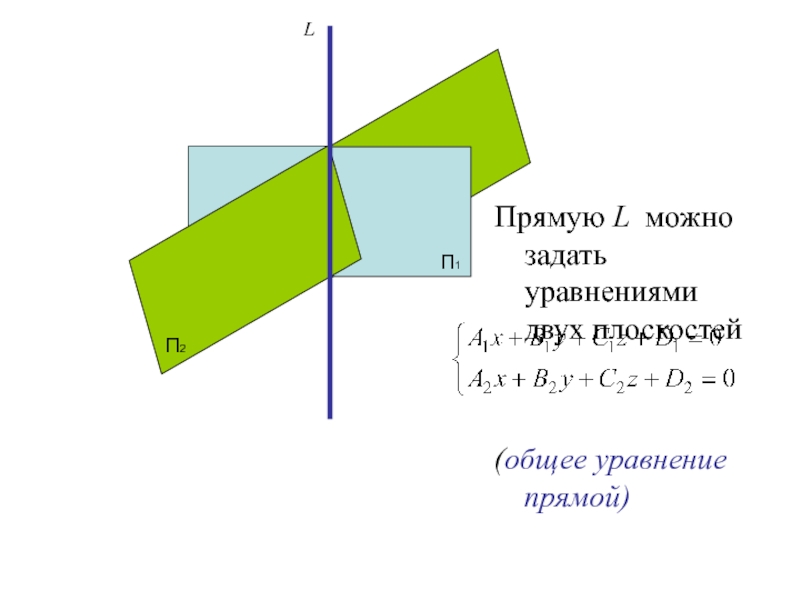
Слайд 33
Прямую L можно задать уравнениями двух плоскостей
(общее уравнение прямой)
П1
П2
L
Слайд 36Приведение к каноническому виду
Решение системы (x0;y0;z0)
Слайд 37Приведение к каноническому виду
Решение системы (x0;y0;z0)⇒ M (x0;y0;z0)∈ L
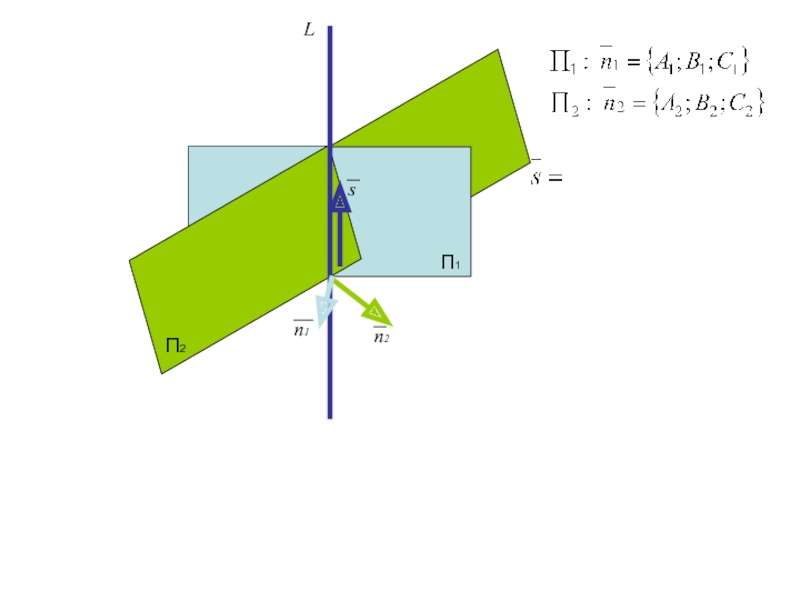
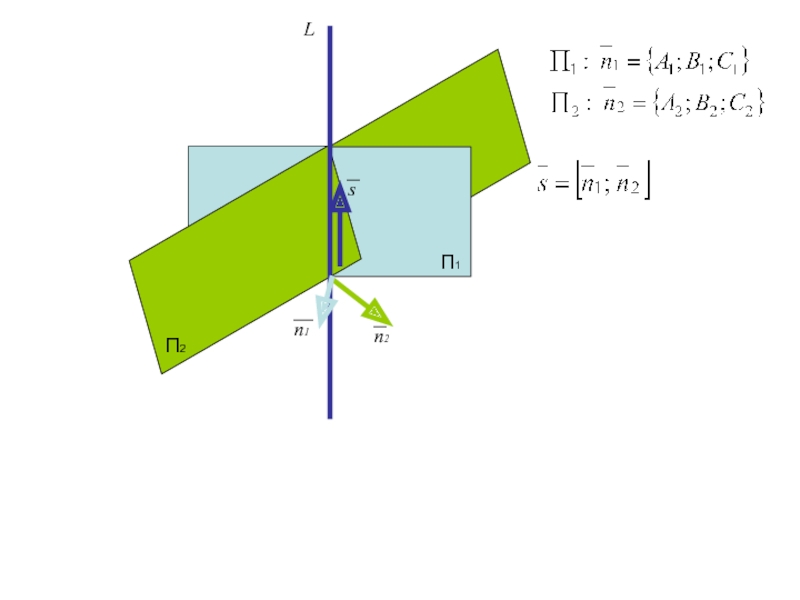
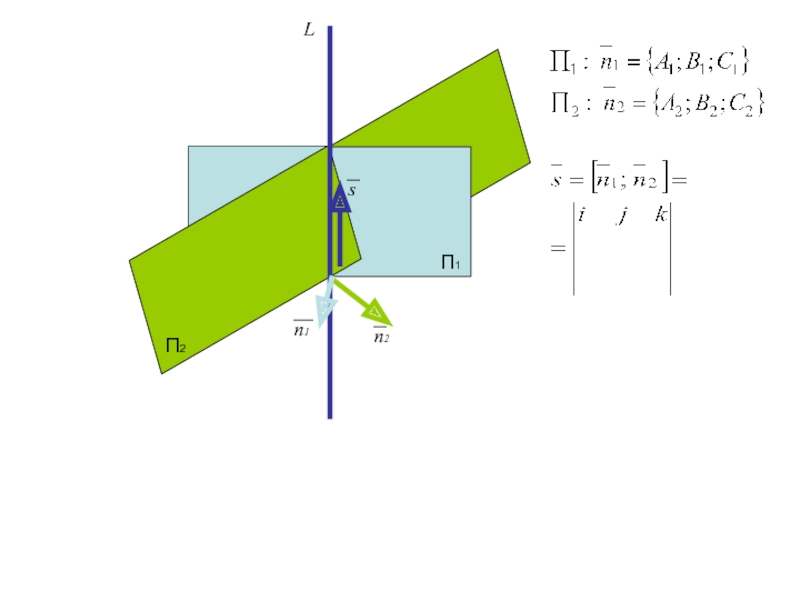
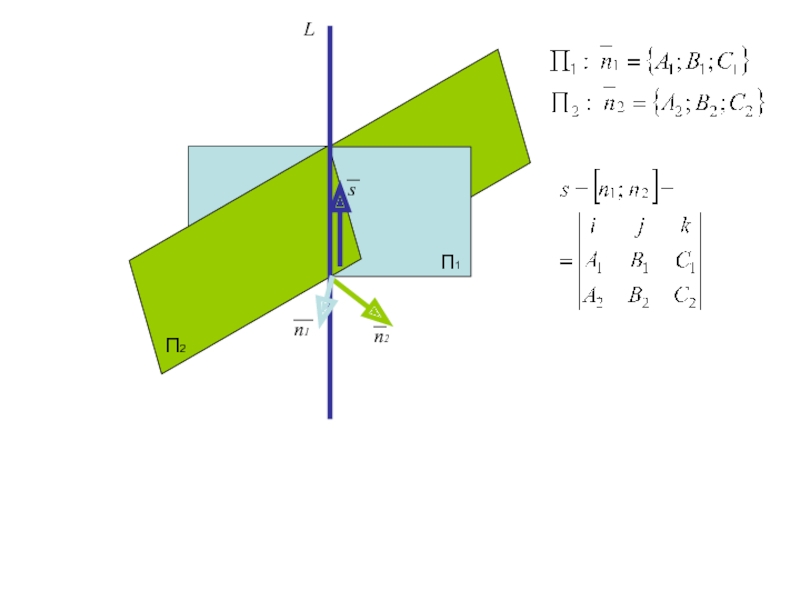
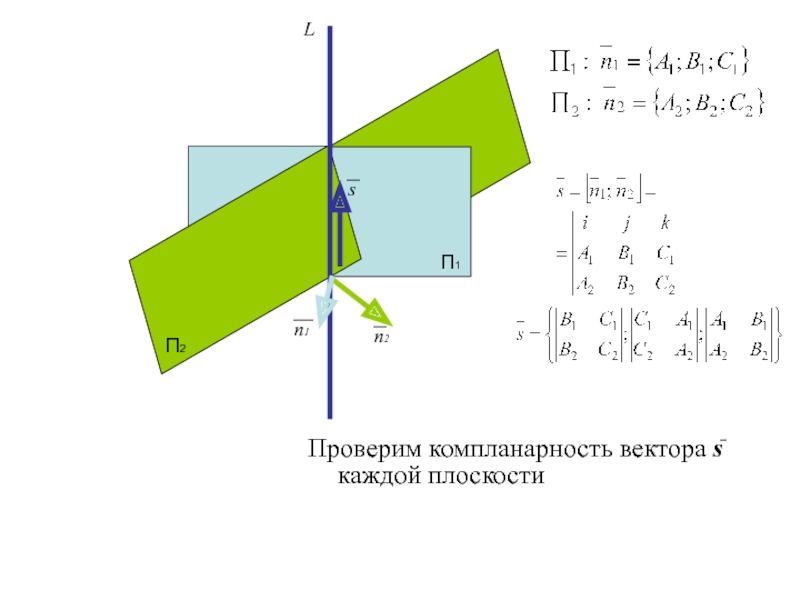
Слайд 47
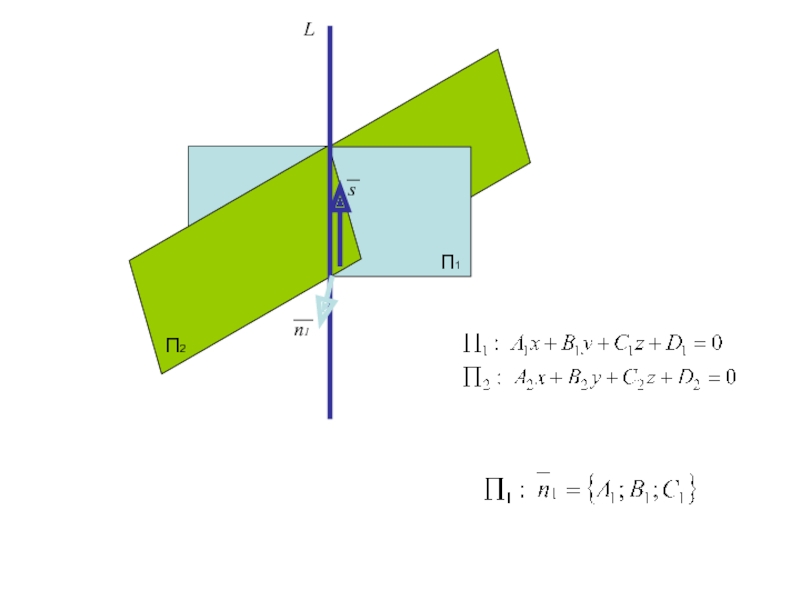
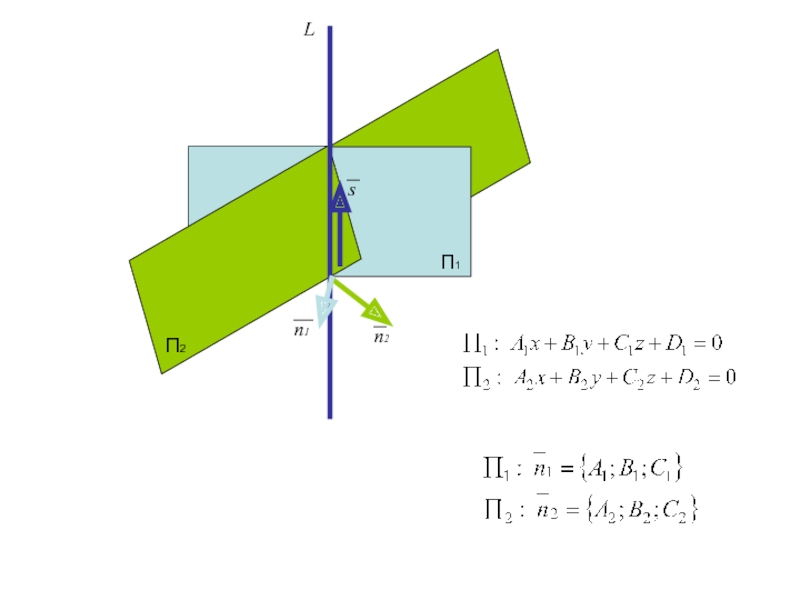
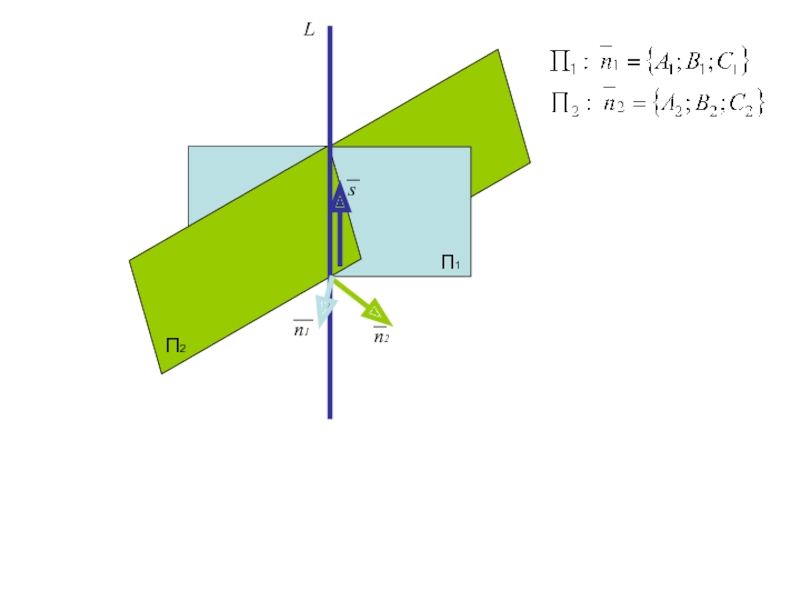
Проверим компланарность вектора s каждой плоскости
П1
П2
L
n2
n1
s
Слайд 48Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости
Ax+By+Cz+D=0
Слайд 49Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости
Ax+By+Cz+D=0
Al+Bm+Cn=0
Слайд 50Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости
Ax+By+Cz+D=0
Al+Bm+Cn=0
Слайд 51Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости
Ax+By+Cz+D=0
Al+Bm+Cn=0
l
m
n
Слайд 52Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости
Ax+By+Cz+D=0
Al+Bm+Cn=0
l
m
n
Слайд 53Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости
Ax+By+Cz+D=0
Al+Bm+Cn=0
l
m
n
Слайд 54Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости
Ax+By+Cz+D=0
Al+Bm+Cn=0
l
m
n
Слайд 55Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости
Ax+By+Cz+D=0
Al+Bm+Cn=0
l
m
n
Слайд 56Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости
Ax+By+Cz+D=0
Al+Bm+Cn=0
l
m
n
Слайд 57имеет канонические уравнения
где M (x0;y0;z0)∈ L
Прямая как пересечение двух плоскостей
Слайд 588. Параллельность прямой плоскости
(1)
: Ax+By+Cz+D=0 (2)
Прямая и плоскость параллельны ⇔
(1)
: Ax+By+Cz+D=0 (2)
Прямая и плоскость параллельны ⇔
Al+Bm+Cn=0,
Ax0+By0+Cz0+D ≠ 0
(1)
: Ax+By+Cz+D=0 (2)
Прямая и плоскость параллельны ⇔
Al+Bm+Cn=0,
Ax0+By0+Cz0+D ≠ 0
↓ L
(1)
: Ax+By+Cz+D=0 (2)
Прямая и плоскость параллельны ⇔
Al+Bm+Cn=0,
Ax0+By0+Cz0+D ≠ 0
L
подставим в (2)
(1)
: Ax+By+Cz+D=0 (2)
Прямая и плоскость параллельны ⇔
Al+Bm+Cn=0,
Ax0+By0+Cz0+D ≠ 0
L
подставим в (2)
A(x0+lt)+B(y0+mt)+C(z0+nt)+D=0
(1)
: Ax+By+Cz+D=0 (2)
Прямая и плоскость параллельны ⇔
Al+Bm+Cn=0,
Ax0+By0+Cz0+D ≠ 0
L
подставим в (2)
A(x0+lt)+B(y0+mt)+C(z0+nt)+D=0
(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Слайд 68(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0
Слайд 69(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
Слайд 70(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
⇒ прямая и плоскость
имеют одну общую точку, т.е. пересекаются
Слайд 71(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
⇒ прямая и плоскость
имеют одну общую точку, т.е. пересекаются
Если Al+Bm+Cn= 0
Слайд 72(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
⇒ прямая и плоскость
имеют одну общую точку, т.е. пересекаются
Если Al+Bm+Cn= 0 , то
Ax0+By0+Cz0+D=0
Слайд 73(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
⇒ прямая и плоскость
имеют одну общую точку, т.е. пересекаются
Если Al+Bm+Cn= 0 , то
Ax0+By0+Cz0+D=0
⇒ ∀ t
Слайд 74(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
⇒ прямая и плоскость
имеют одну общую точку, т.е. пересекаются
Если Al+Bm+Cn= 0 , то
Ax0+By0+Cz0+D=0
⇒ ∀ t, т.е. прямая лежит на плоскости
Слайд 75(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
⇒ прямая и плоскость
имеют одну общую точку, т.е. пересекаются
Если Al+Bm+Cn= 0 , то
Ax0+By0+Cz0+D=0
⇒ ∀ t, т.е. прямая лежит на плоскости
Если Al+Bm+Cn= 0 , то Ax0+By0+Cz0+D≠ 0
Слайд 76(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
⇒ прямая и плоскость
имеют одну общую точку, т.е. пересекаются
Если Al+Bm+Cn= 0 , то
Ax0+By0+Cz0+D=0
⇒ ∀ t, т.е. прямая лежит на плоскости
Если Al+Bm+Cn= 0 , то Ax0+By0+Cz0+D≠ 0
⇒ ∃ t,
Слайд 77(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
⇒ прямая и плоскость
имеют одну общую точку, т.е. пересекаются
Если Al+Bm+Cn= 0 , то
Ax0+By0+Cz0+D=0
⇒ ∀ t, т.е. прямая лежит на плоскости
Если Al+Bm+Cn= 0 , то Ax0+By0+Cz0+D≠ 0
⇒ ∃ t, т.е. на данной прямой нет ни одной точки, лежащей на данной плоскости
↑
Слайд 78(Al+Bm+Cn)t+ Ax0+By0+Cz0+D=0
Если Al+Bm+Cn≠ 0 , то
⇒ прямая и плоскость
имеют одну общую точку, т.е. пересекаются
Если Al+Bm+Cn= 0 , то
Ax0+By0+Cz0+D=0
⇒ ∀ t, т.е. прямая лежит на плоскости
Если Al+Bm+Cn= 0 , то Ax0+By0+Cz0+D≠ 0
⇒ ∃ t, т.е. на данной прямой нет ни одной точки, лежащей на данной плоскости, прямая параллельна плоскости
↑
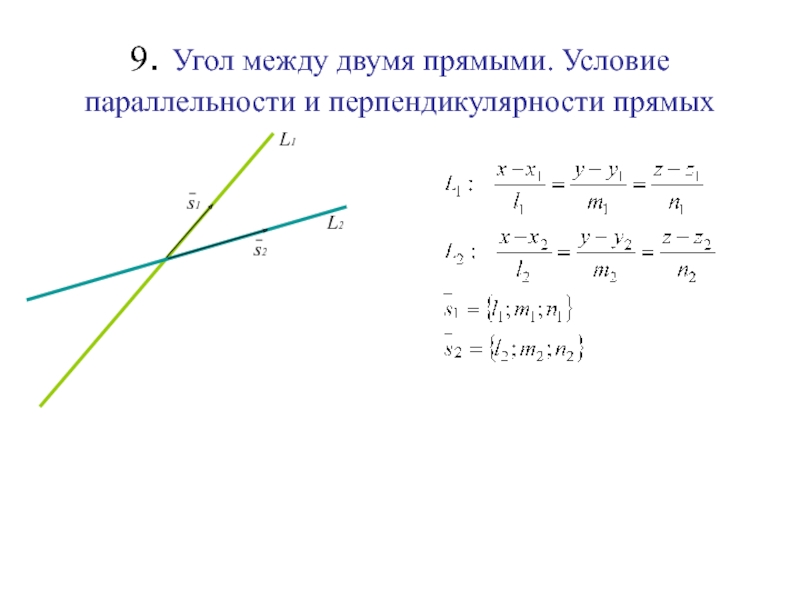
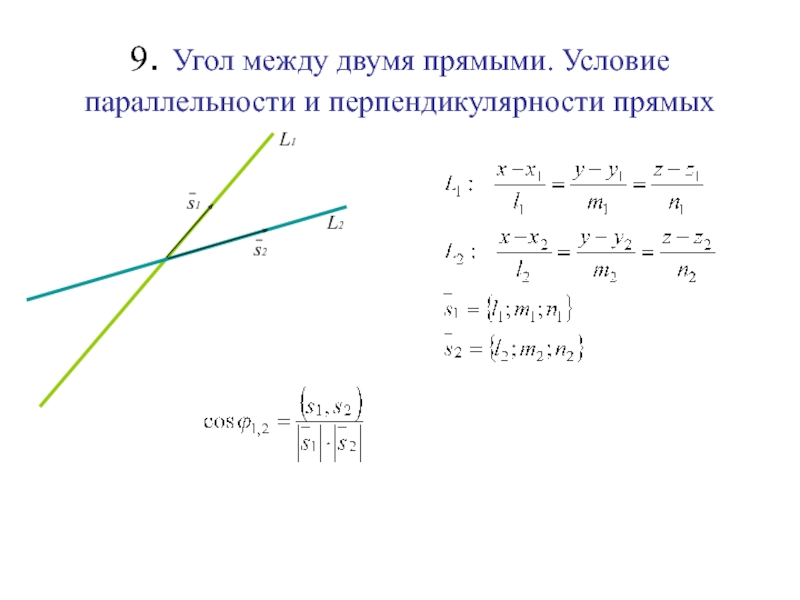
Слайд 799. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
Слайд 809. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
Слайд 819. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
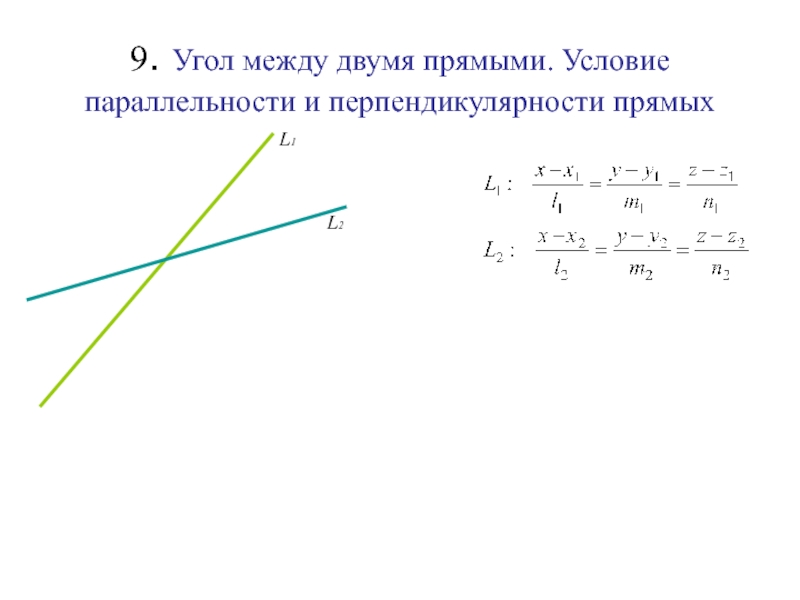
L1
L2
Слайд 829. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
L2
Слайд 839. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
L2
Слайд 849. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
L2
Слайд 859. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
L2
Слайд 869. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
L2
Слайд 879. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
L2
Слайд 889. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
L2
Слайд 899. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
L2
Слайд 909. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
L1
L2
Слайд 919. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
(угол
между двумя прямыми L1 и L2)
L1
L2
Слайд 92Условие перпендикулярности прямых L1 и L2
Слайд 93Условие перпендикулярности прямых L1 и L2
Слайд 94Условие перпендикулярности прямых L1 и L2
Слайд 95Условие перпендикулярности прямых L1 и L2
Слайд 96Условие перпендикулярности прямых L1 и L2
Условие параллельности прямых L1 и
L2
Слайд 97Условие перпендикулярности прямых L1 и L2
Условие параллельности прямых L1 и
Слайд 98Условие перпендикулярности прямых L1 и L2
Условие параллельности прямых L1 и
Слайд 99Условие перпендикулярности прямых L1 и L2
Условие параллельности прямых L1 и
Слайд 10010. Условие принадлежности двух прямых к одной плоскости
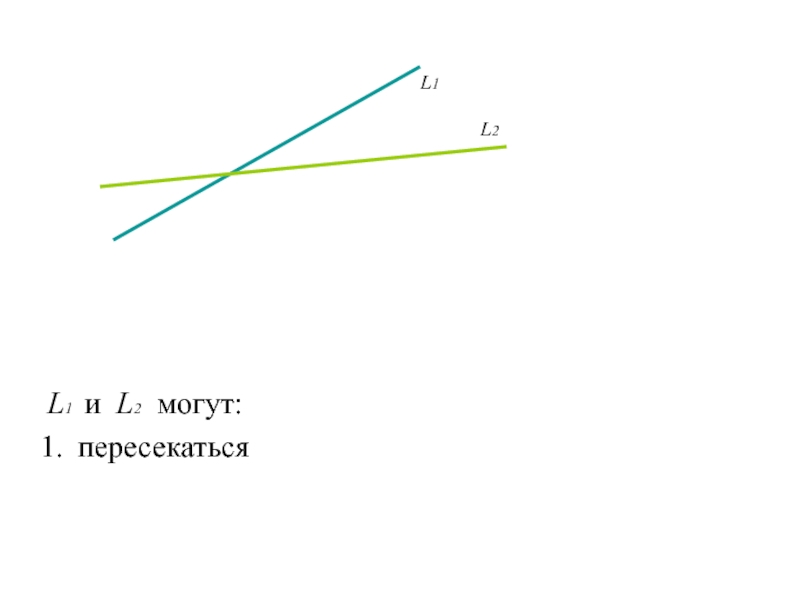
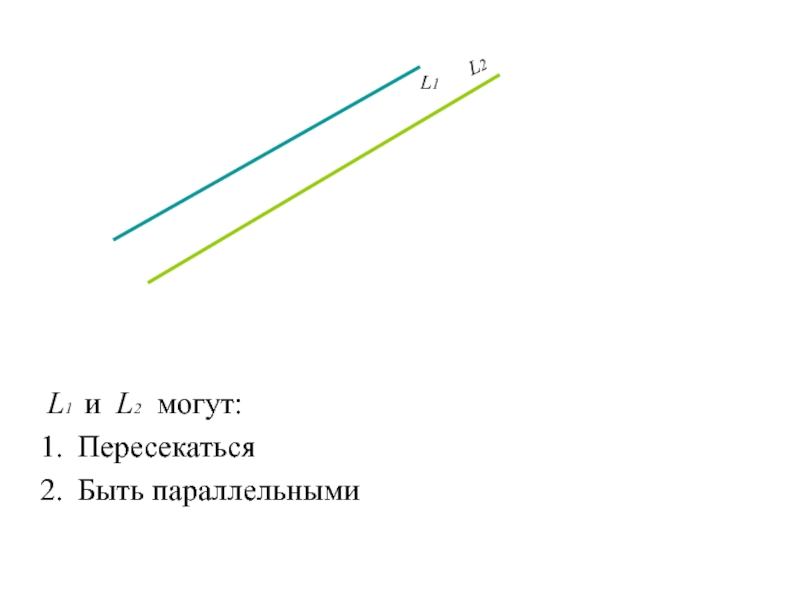
Слайд 104L1 и L2 могут:
Пересекаться
Быть параллельными
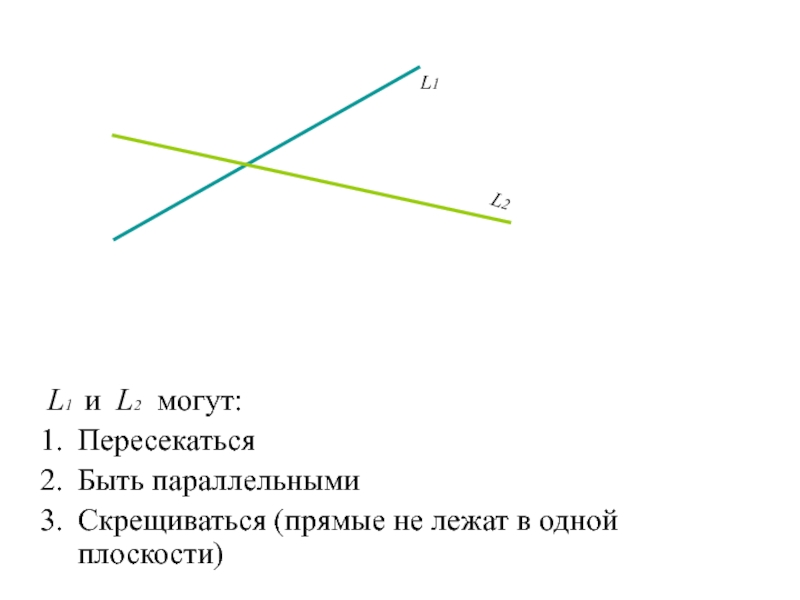
Слайд 105L1 и L2 могут:
Пересекаться
Быть параллельными
Скрещиваться (прямые не лежат в
одной плоскости)
Слайд 106
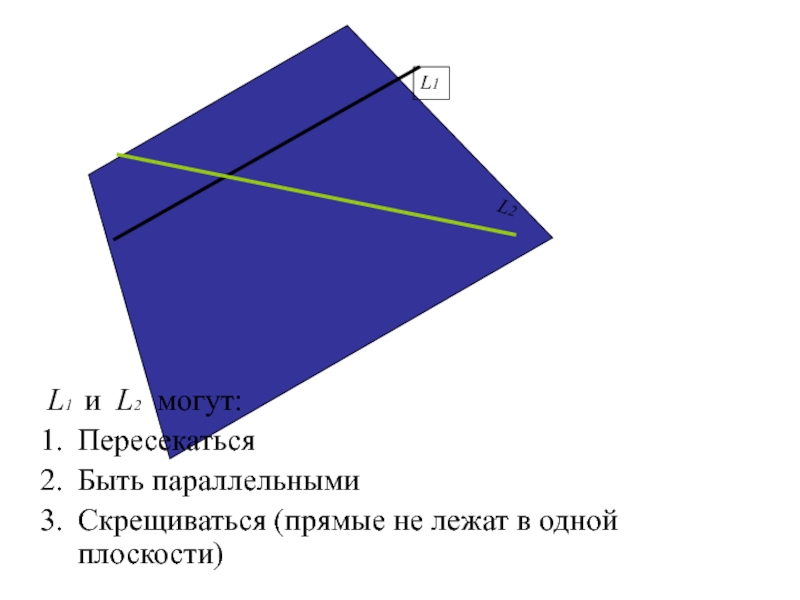
L1 и L2 могут:
Пересекаться
Быть параллельными
Скрещиваться (прямые не лежат в
одной плоскости)
Слайд 107
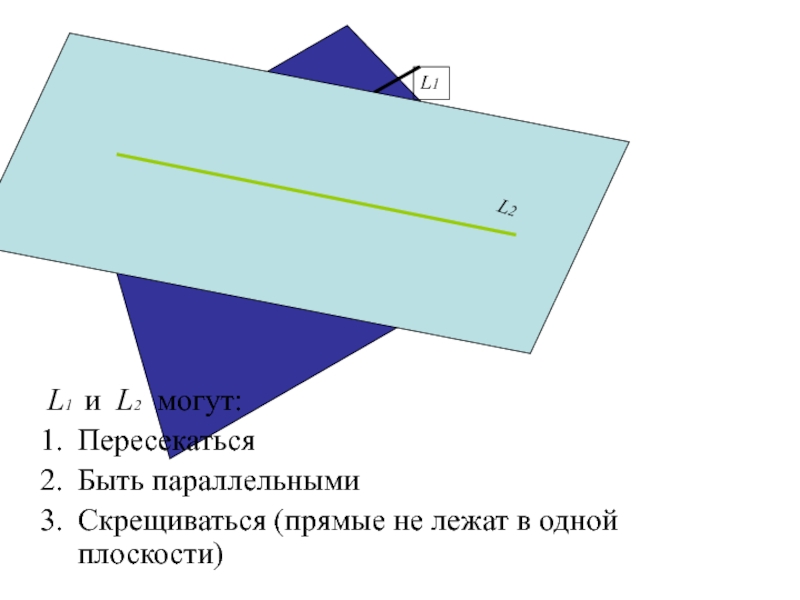
L1 и L2 могут:
Пересекаться
Быть параллельными
Скрещиваться (прямые не лежат в
одной плоскости)
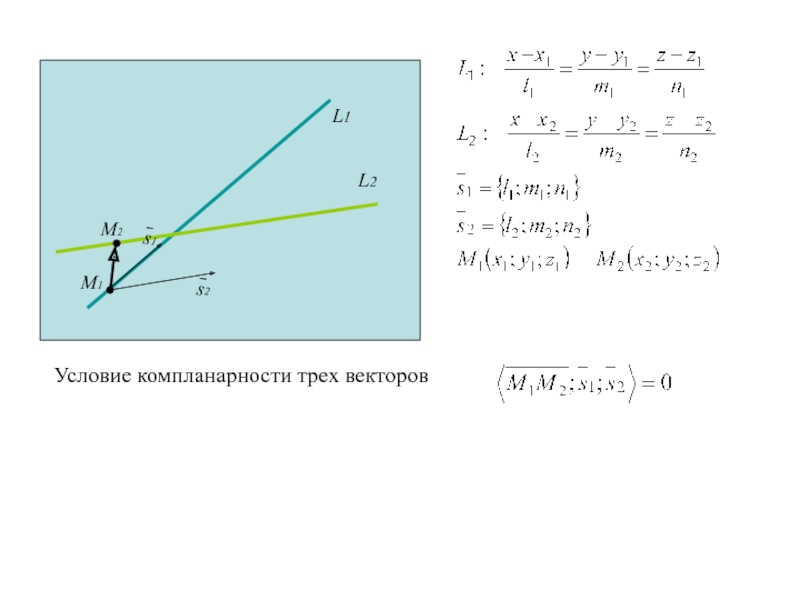
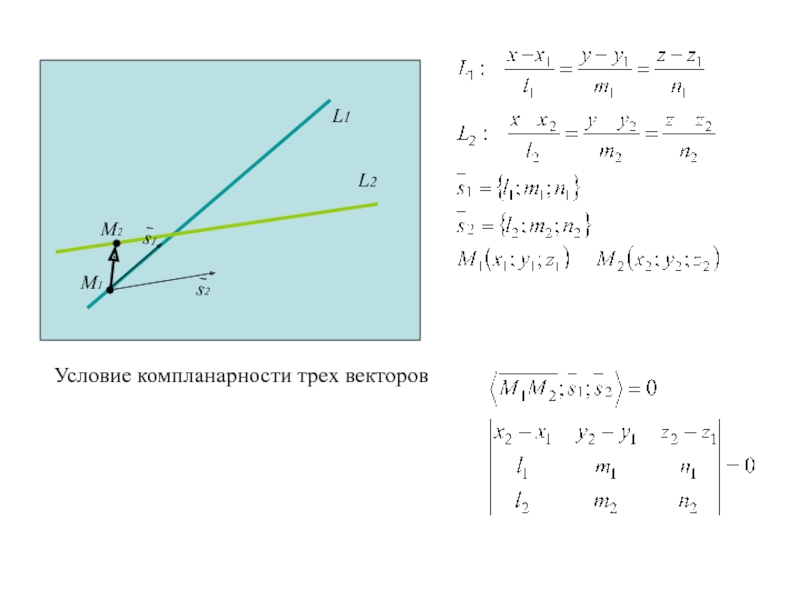
Слайд 117Условие компланарности трех векторов
М1
М2
Слайд 118Условие компланарности трех векторов
М1
М2
Слайд 119Условие принадлежности двух прямых L1 и L2 одной плоскости
Слайд 120Условие принадлежности двух прямых L1 и L2 одной плоскости
Условие параллельности
L1 и L2
Слайд 12111. Геометрический смысл неравенства первой степени с тремя неизвестными
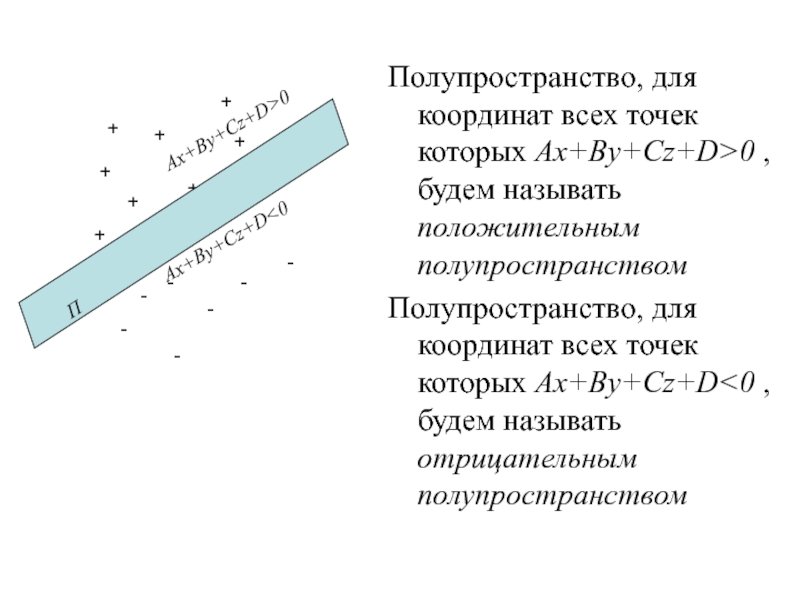
Слайд 122Теорема: Пусть относительно ДПСК плоскость задана общим уравнением Ax+By+Cz+D=0. Тогда
для координат (x,y,z) всех точек, лежащих по одну сторону от
этой плоскости выполняется неравенство Ax+By+Cz+D>0, а для координат (x,y,z) всех точек, лежащих по другую сторону от этой плоскости выполняется неравенство Ax+By+Cz+D<0
Слайд 123Полупространство, для координат всех точек которых Ax+By+Cz+D>0 , будем называть
положительным полупространством
Полупространство, для координат всех точек которых Ax+By+Cz+D
называть отрицательным полупространством
+
+
+
+
+
+
+
+
Ax+By+Cz+D>0
Ax+By+Cz+D<0
-
-
-
-
-
-
-
Слайд 124Теорема: Пусть относительно ДПСК плоскость задана общим уравнением Ax+By+Cz+D=0. Тогда
если отложить нормальный вектор этой плоскости от любой точки этой
плоскости, то конец отложенного вектора будет находиться в положительном полупространстве от данной плоскости
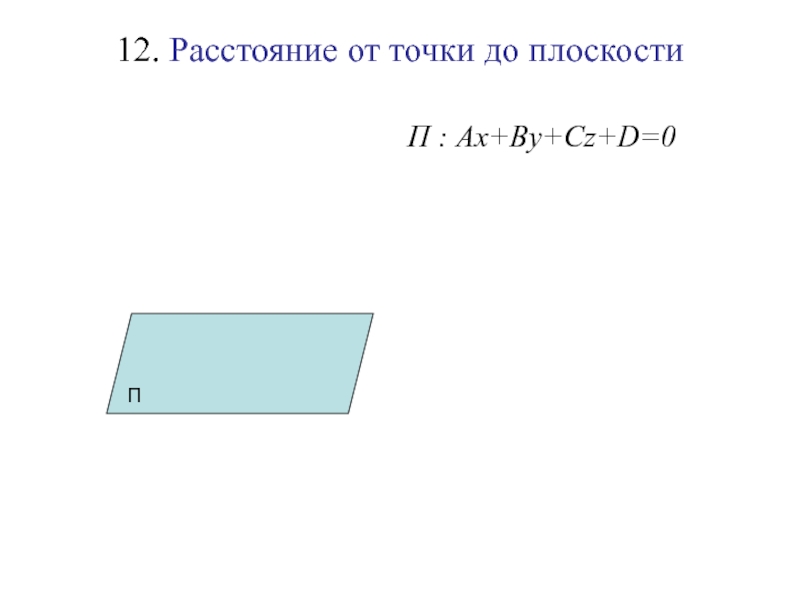
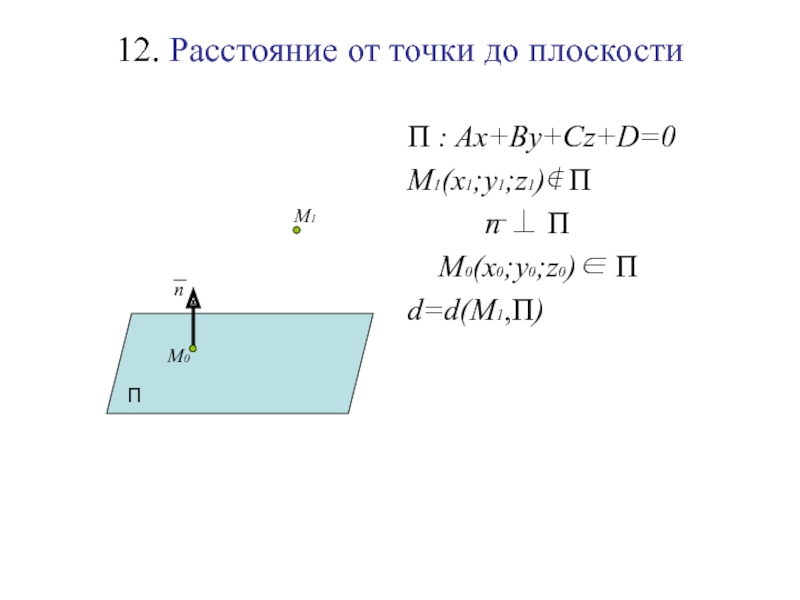
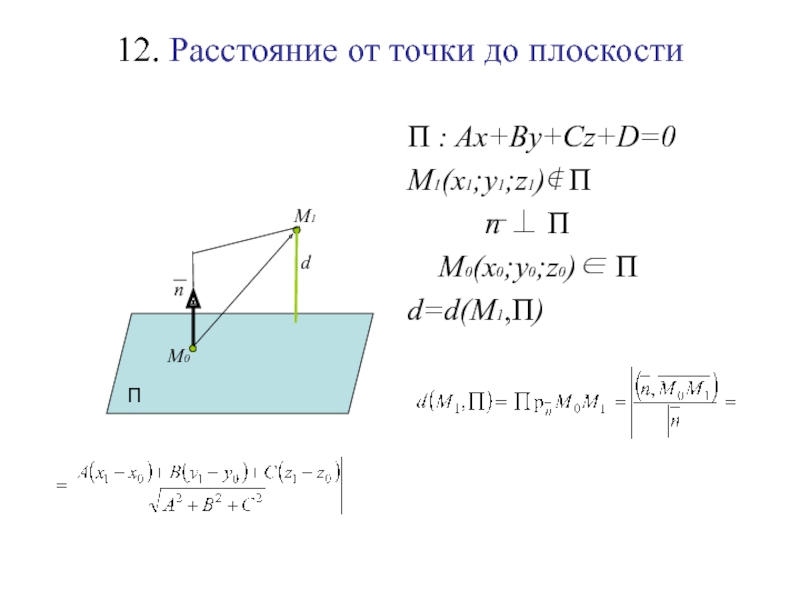
Слайд 12512. Расстояние от точки до плоскости
Слайд 12612. Расстояние от точки до плоскости
П
Слайд 12712. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
П
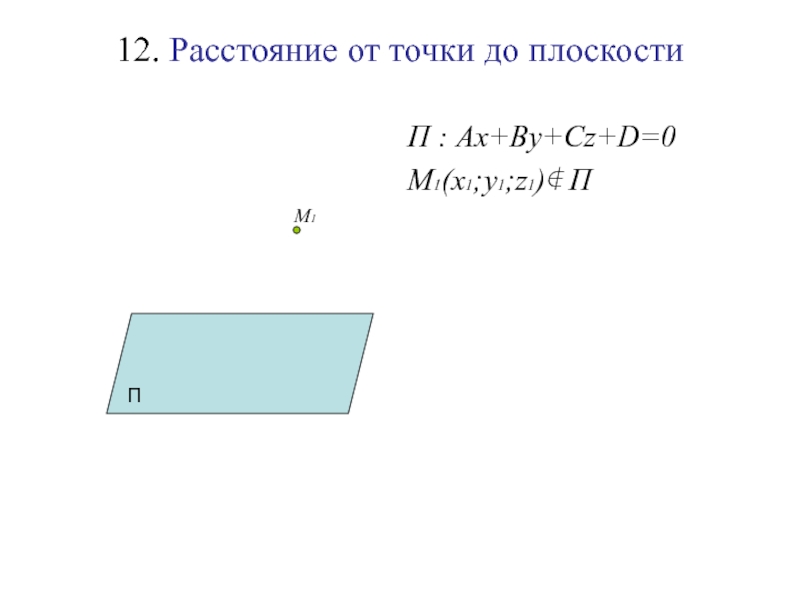
Слайд 12812. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
П
М1
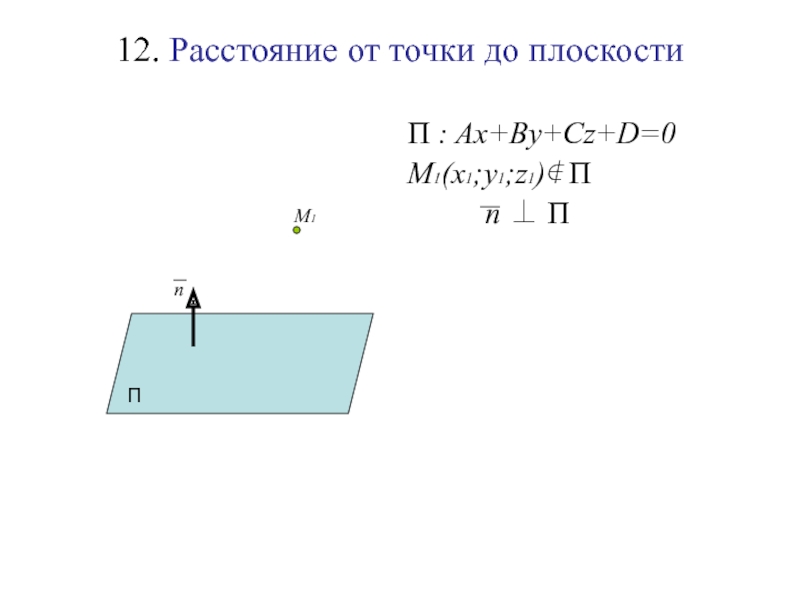
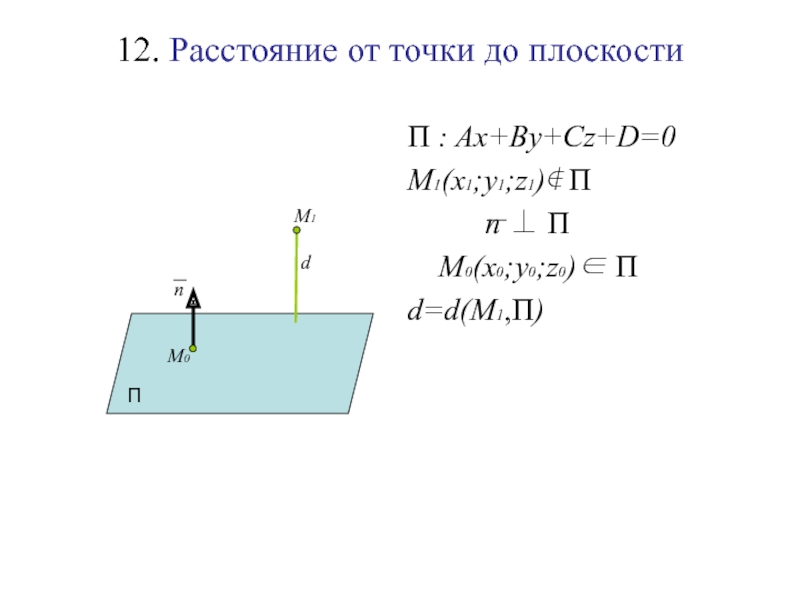
Слайд 12912. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
П
М1
n
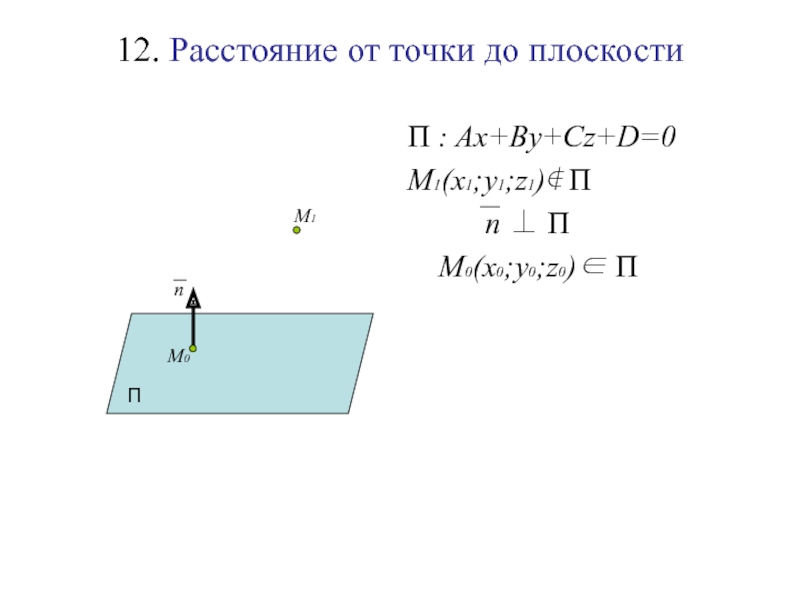
Слайд 13012. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
M0(x0;y0;z0)∈ П
П
n
М0
Слайд 13112. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
M0(x0;y0;z0)∈ П
d=d(M1,П)
П
n
М0
Слайд 13212. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
M0(x0;y0;z0)∈ П
d=d(M1,П)
П
n
М0
d
Слайд 13312. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
M0(x0;y0;z0)∈ П
d=d(M1,П)
П
n
М0
d
Слайд 13412. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
M0(x0;y0;z0)∈ П
d=d(M1,П)
П
n
М0
d
Слайд 13512. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
M0(x0;y0;z0)∈ П
d=d(M1,П)
П
n
М0
d
Слайд 13612. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
M0(x0;y0;z0)∈ П
d=d(M1,П)
П
n
М0
d
Слайд 13712. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
M0(x0;y0;z0)∈ П
d=d(M1,П)
П
n
М0
d
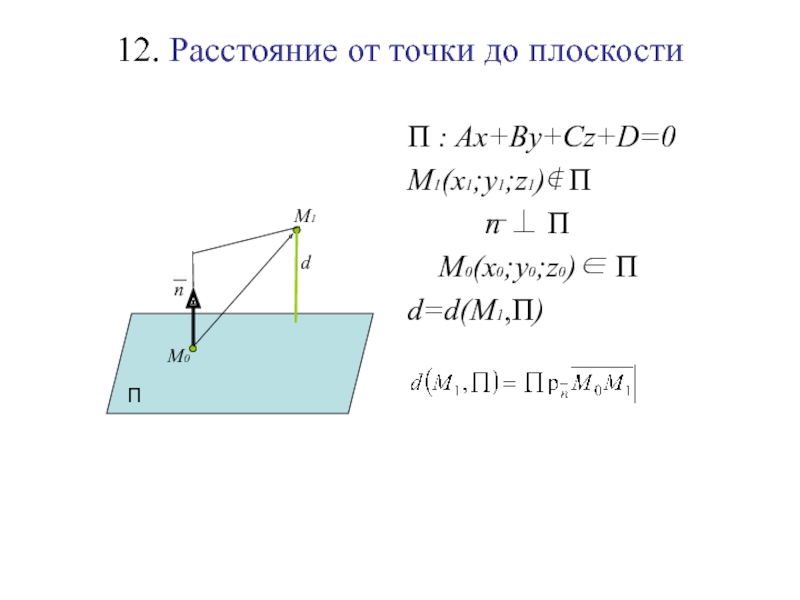
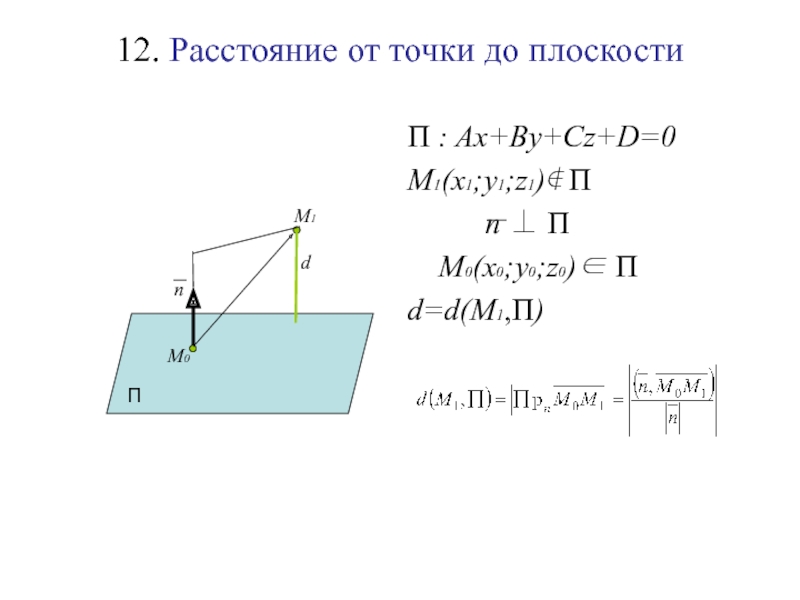
Слайд 13812. Расстояние от точки до плоскости
П : Ax+By+Cz+D=0
M1(x1;y1;z1)∉ П
n ⊥ П
M0(x0;y0;z0)∈ П
d=d(M1,П)
П
n
М0
d
т.к.
M0(x0;y0;z0)∈ П ⇒ Ax0+By0+Cz0+D=0
Слайд 139 Расстояние от точки M1(x1;y1;z1)
до плоскости Ax+By+Cz+D=0
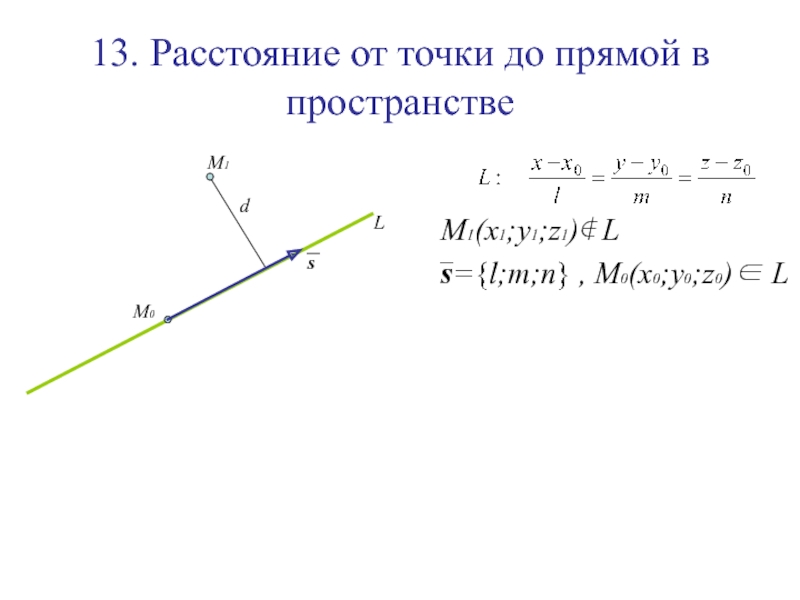
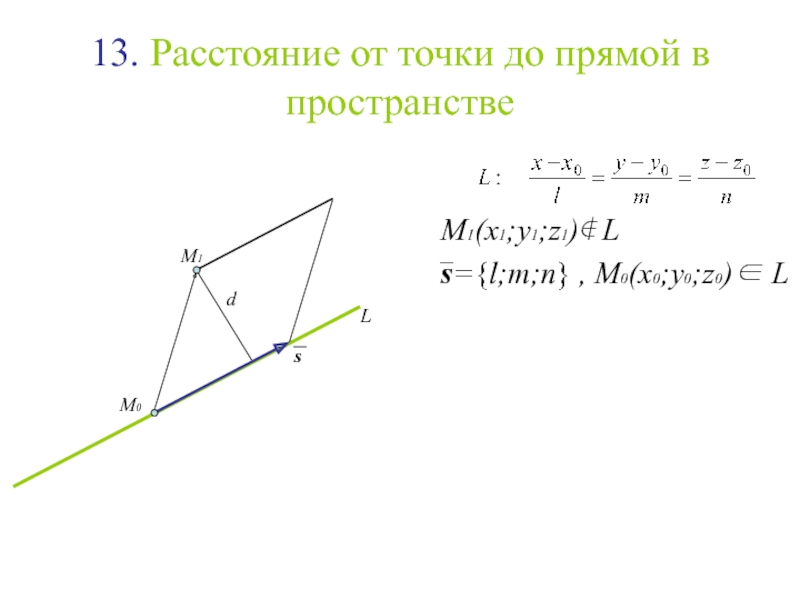
Слайд 14013. Расстояние от точки до прямой в пространстве
Слайд 14113. Расстояние от точки до прямой в пространстве
L
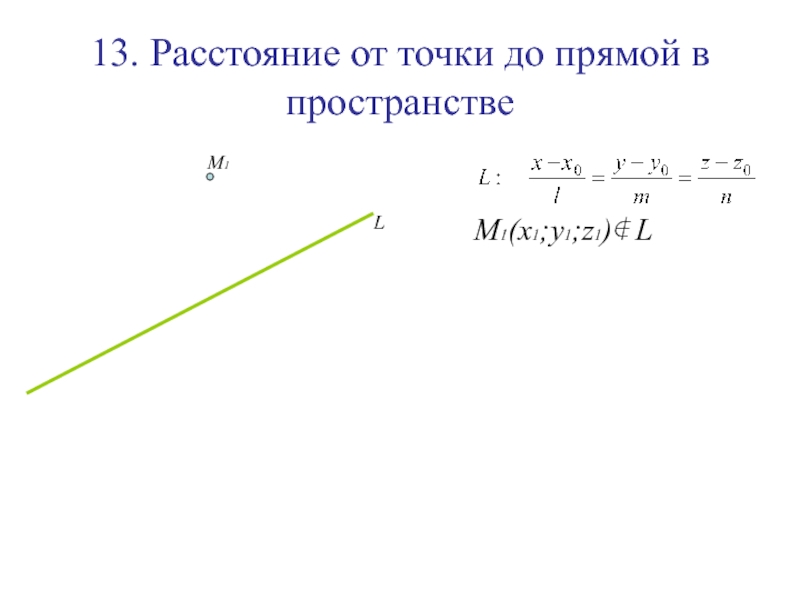
Слайд 14213. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
L
M1
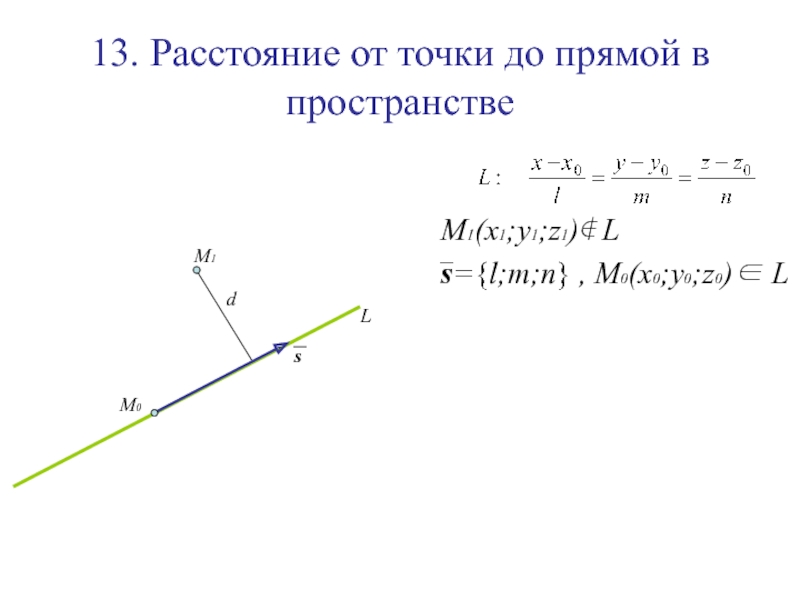
Слайд 14313. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
L
M1
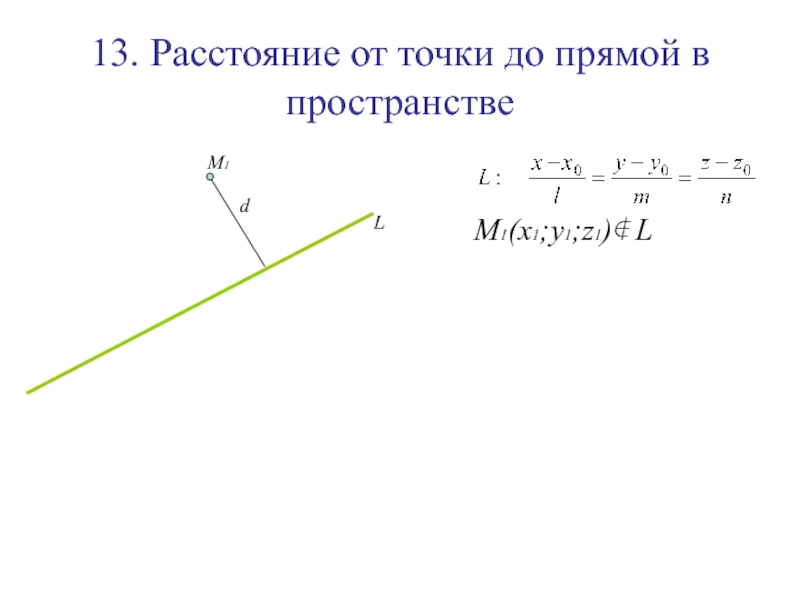
Слайд 14413. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
L
M1
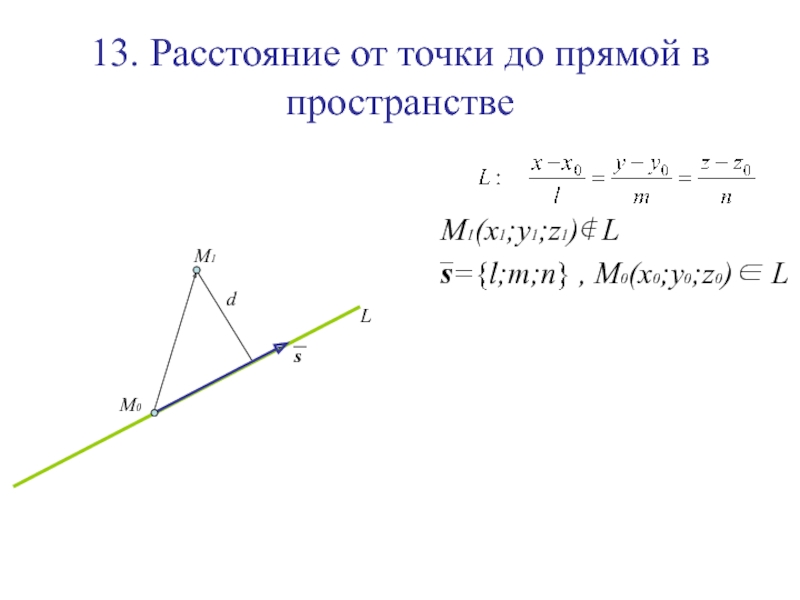
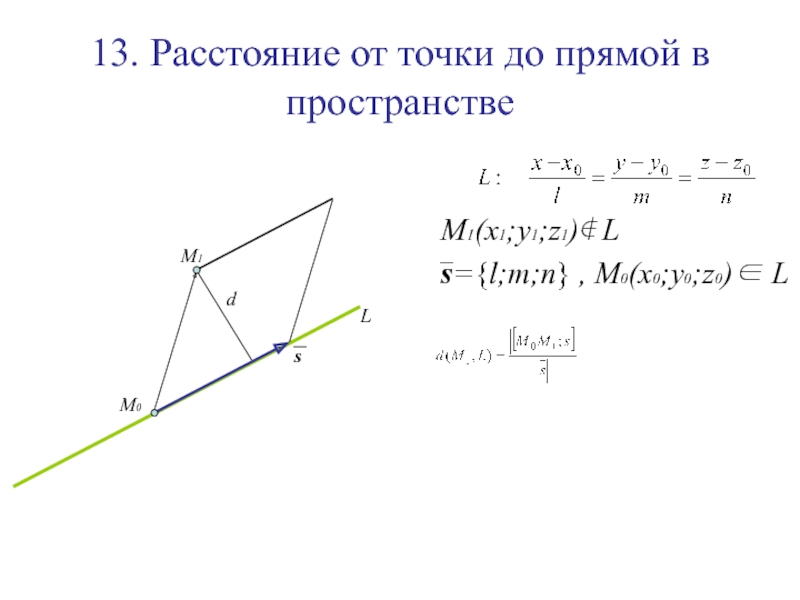
Слайд 14513. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
L
M1
M0
Слайд 14613. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
L
M1
M0
s
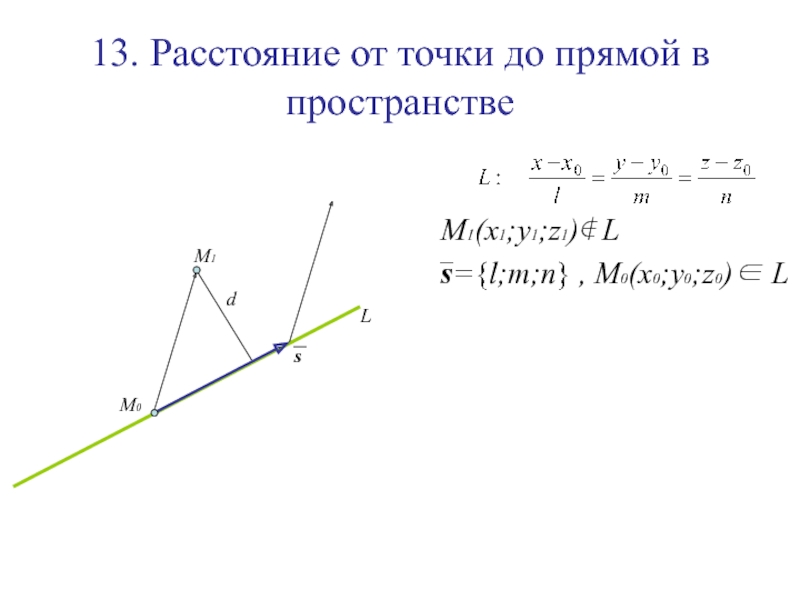
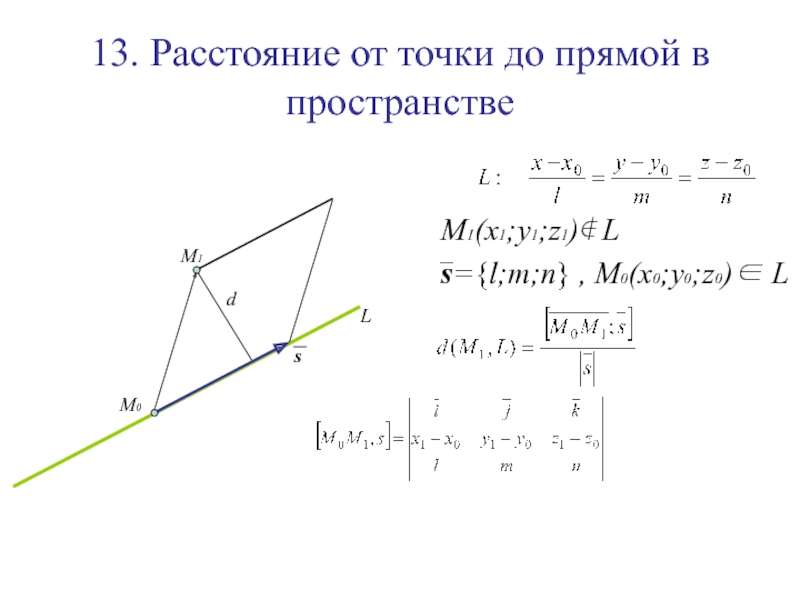
Слайд 14713. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
Слайд 14813. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
Слайд 14913. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
Слайд 15013. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
L
M1
M0
s
Слайд 15113. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
L
M1
M0
s
Слайд 15213. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
L
M1
M0
s
Слайд 15313. Расстояние от точки до прямой в пространстве
M1(x1;y1;z1)∉ L
s={l;m;n} ,
M0(x0;y0;z0)∈ L
L
M1
M0
s
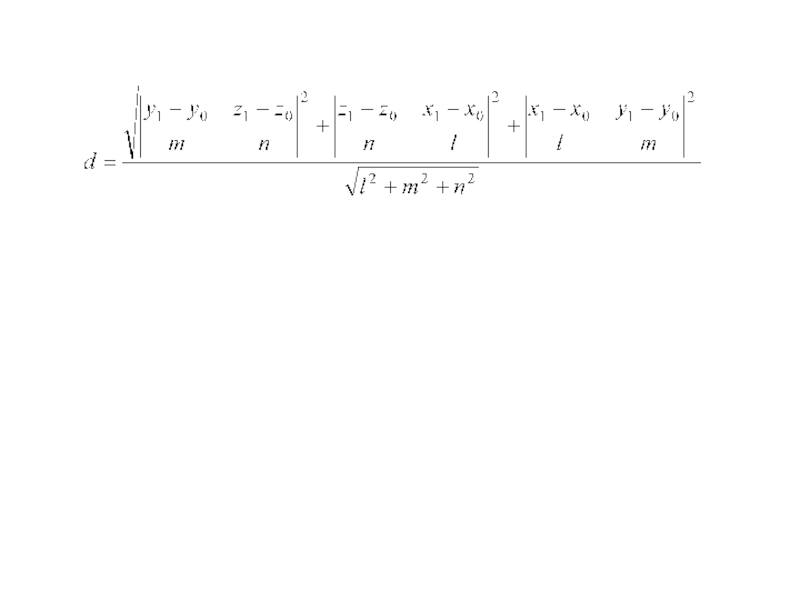
Слайд 155 Расстояние от точки M1(x1;y1;z1) до прямой
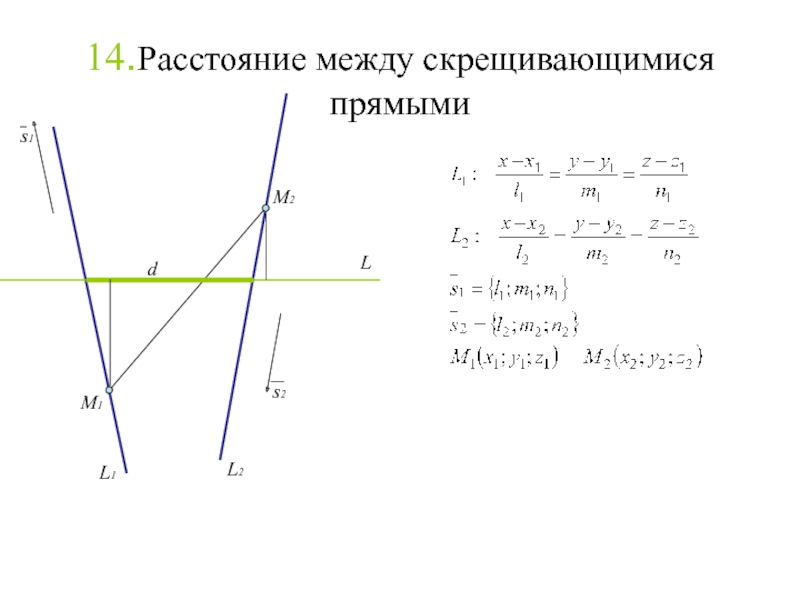
Слайд 15614.Расстояние между скрещивающимися прямыми
Слайд 15714.Расстояние между скрещивающимися прямыми
Слайд 15814.Расстояние между скрещивающимися прямыми
Слайд 15914.Расстояние между скрещивающимися прямыми
M1
M2
s1
s2
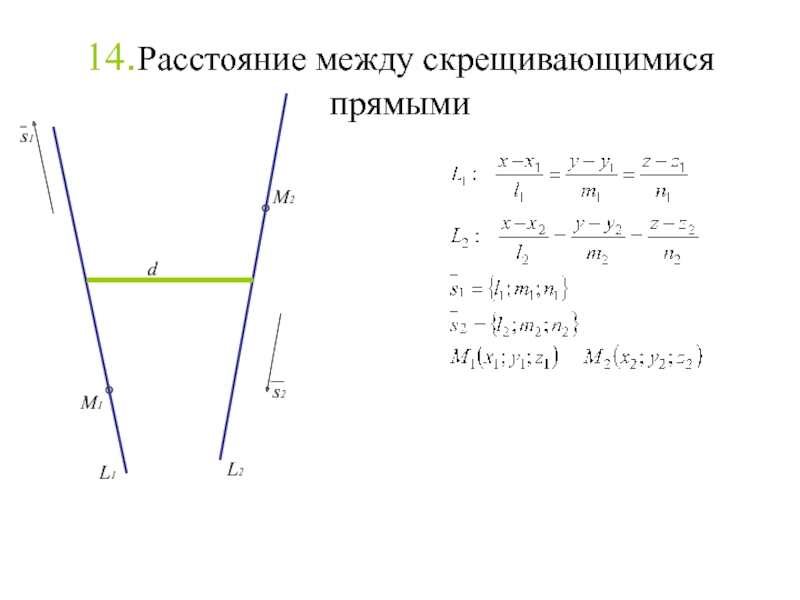
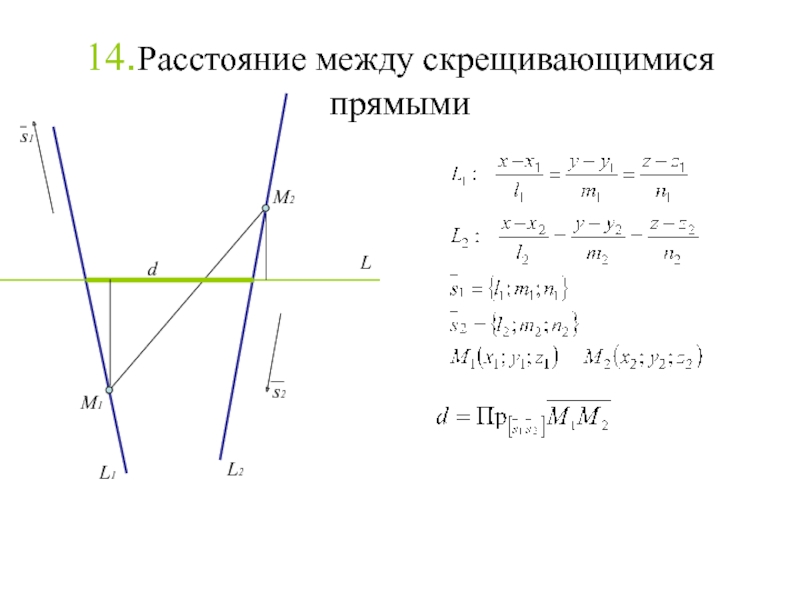
Слайд 16014.Расстояние между скрещивающимися прямыми
M1
M2
s1
s2
d
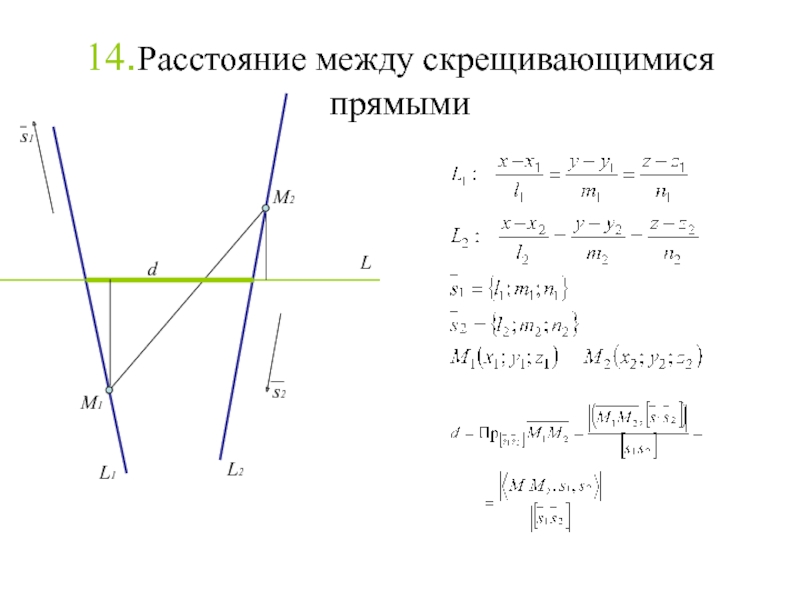
Слайд 16114.Расстояние между скрещивающимися прямыми
M1
M2
s1
s2
d
Слайд 16214.Расстояние между скрещивающимися прямыми
M1
M2
s1
s2
d
L
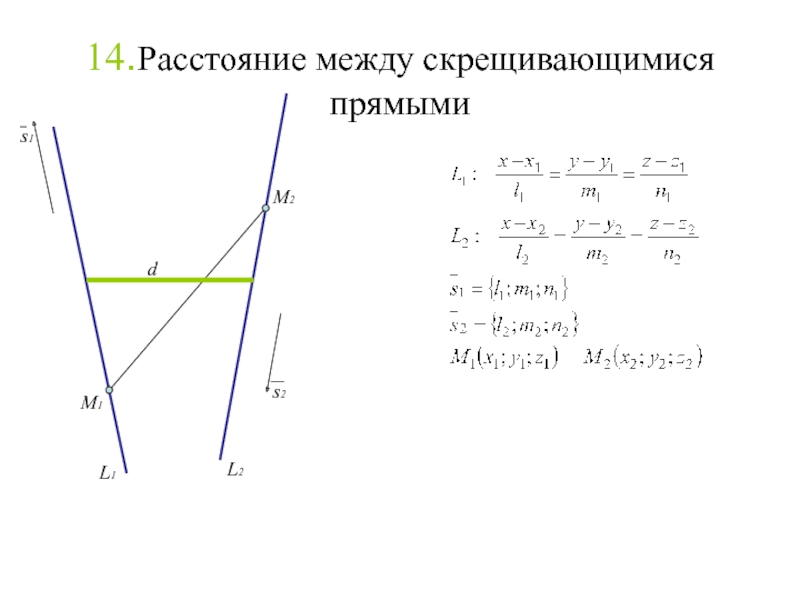
Слайд 16314.Расстояние между скрещивающимися прямыми
M1
M2
s1
s2
d
L
Слайд 16414.Расстояние между скрещивающимися прямыми
M1
M2
s1
s2
d
L
Слайд 16514.Расстояние между скрещивающимися прямыми
M1
M2
s1
s2
d
L
Слайд 168Расстояние между скрещивающимися прямыми
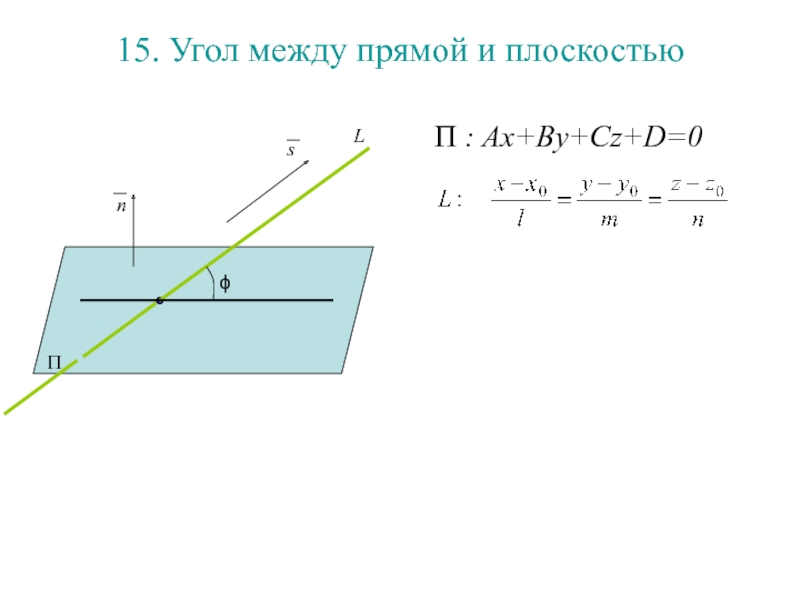
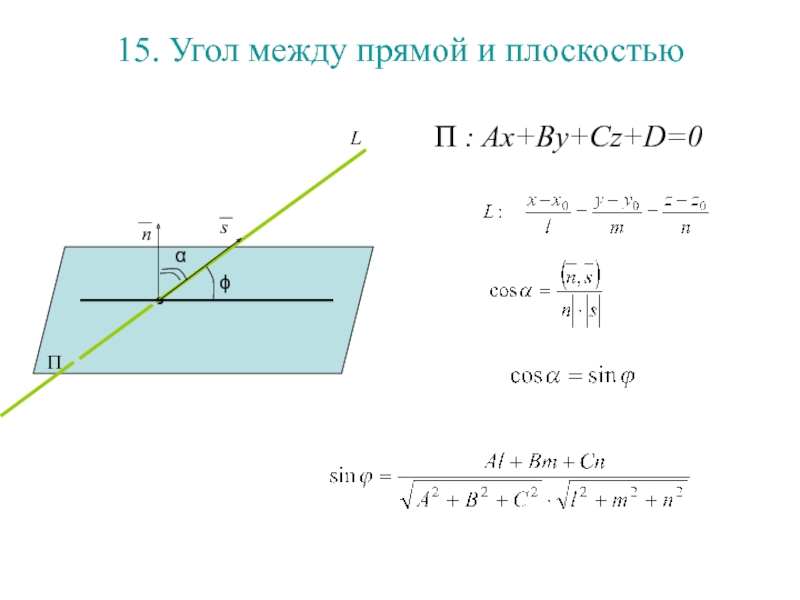
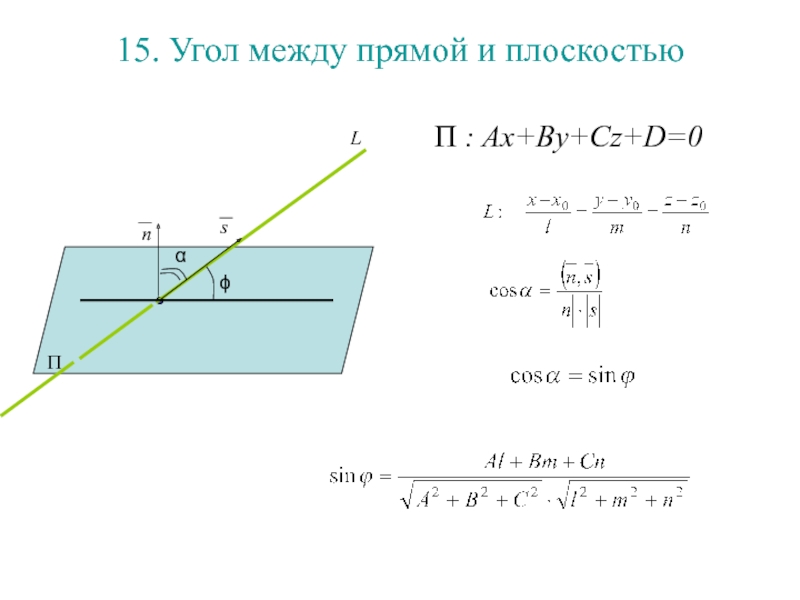
Слайд 17015. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
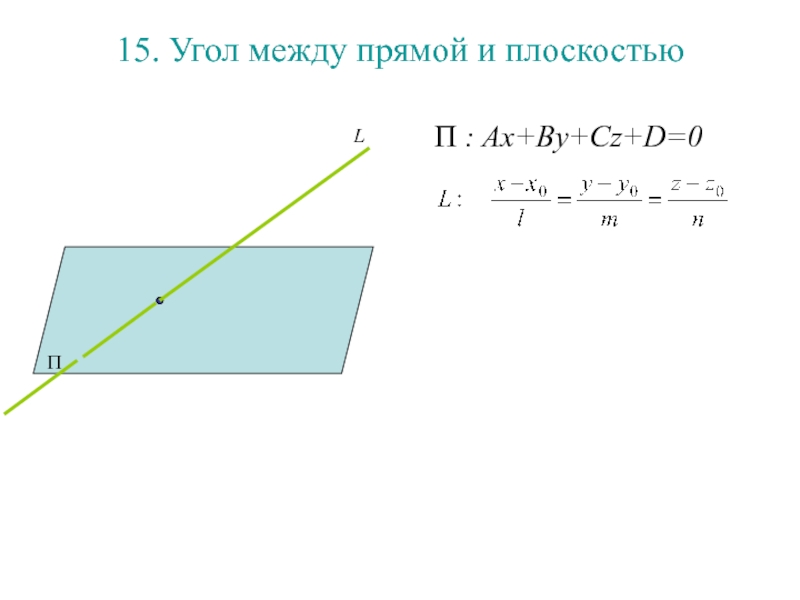
Слайд 17115. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
Слайд 17215. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
ϕ
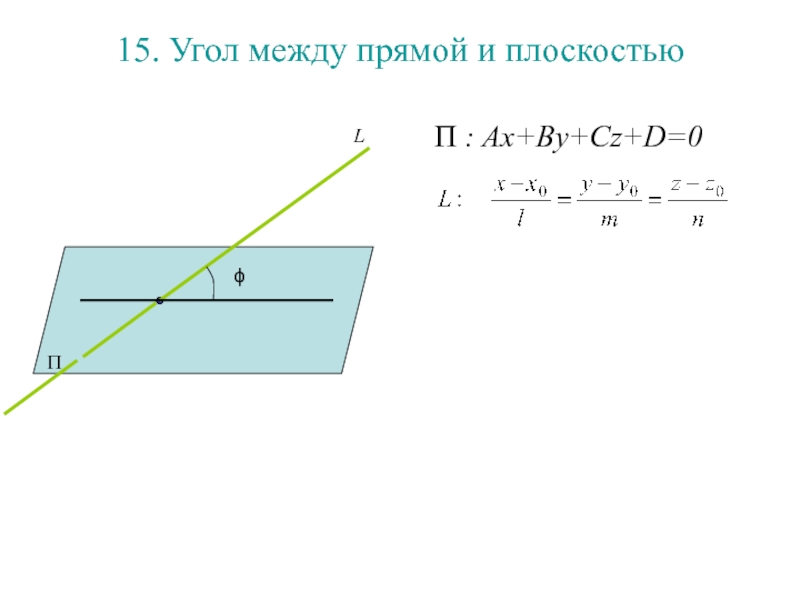
Слайд 17315. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
ϕ
Слайд 17415. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
ϕ
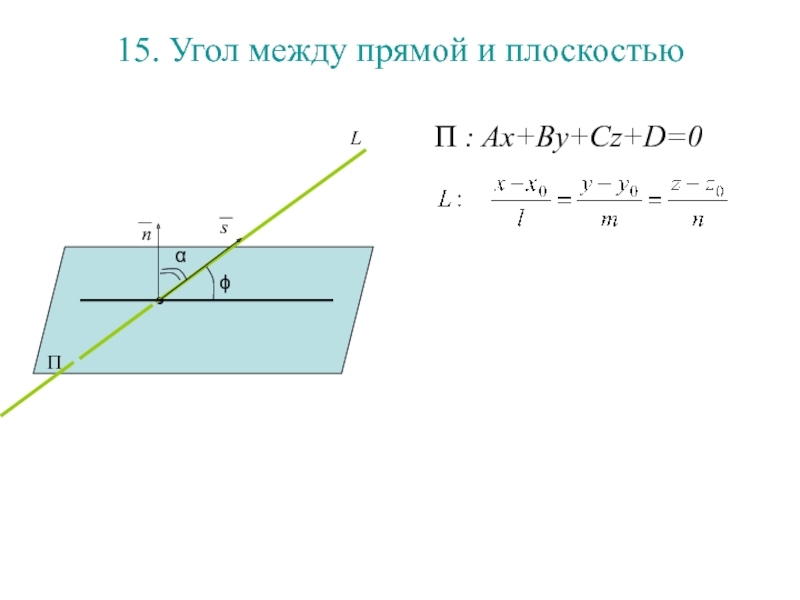
Слайд 17515. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
ϕ
α
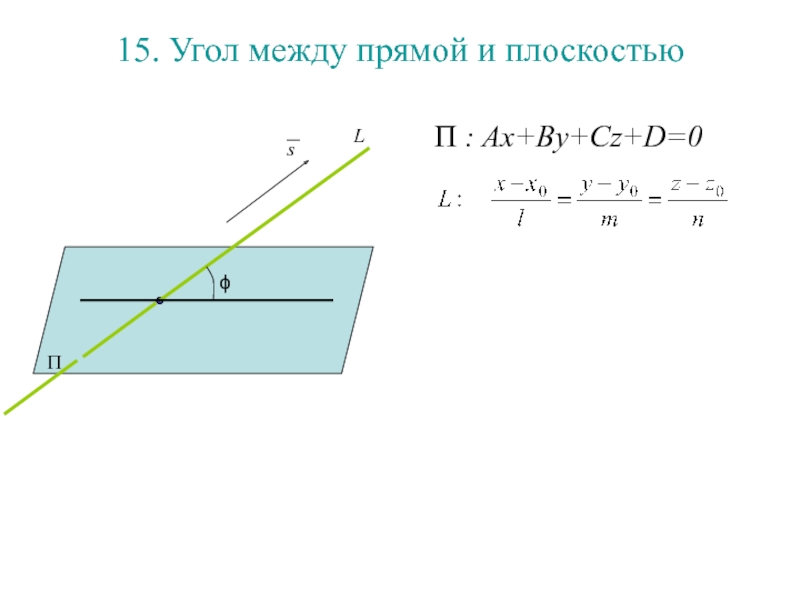
Слайд 17615. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
ϕ
α
Слайд 17715. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
ϕ
α
Слайд 17815. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
ϕ
α
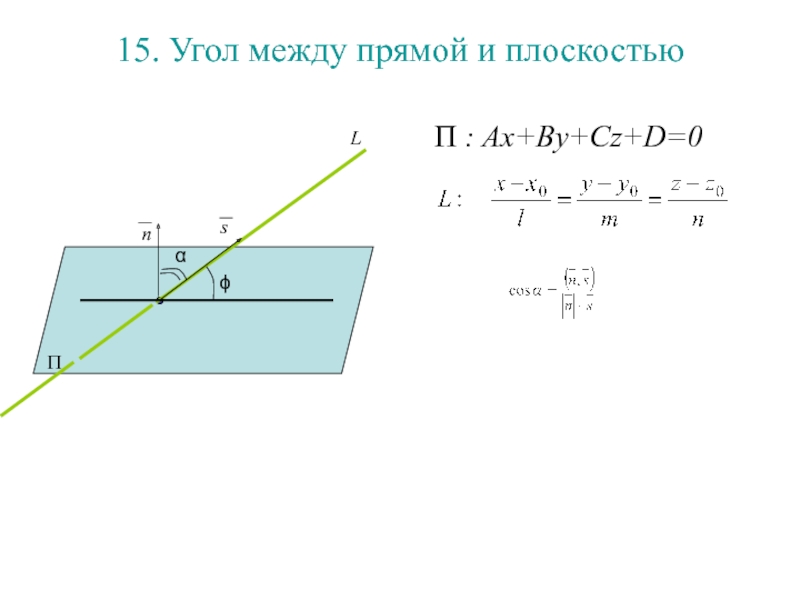
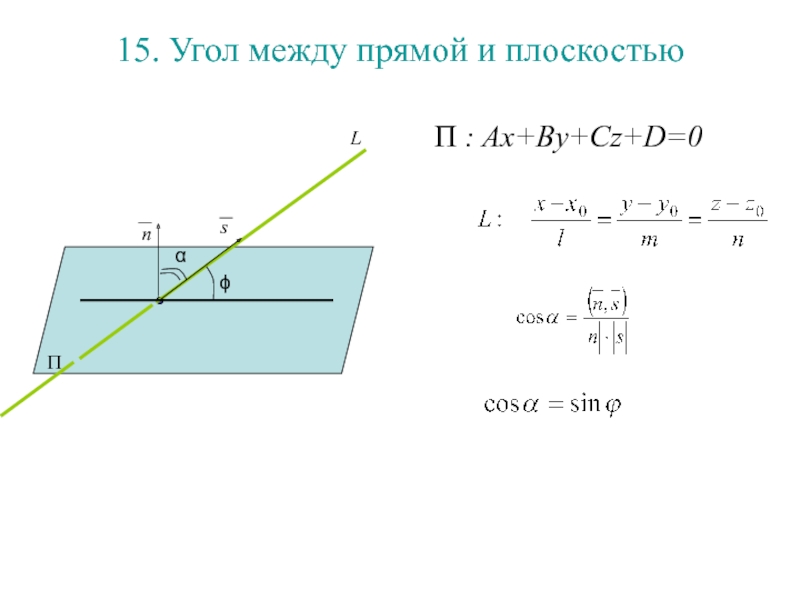
Слайд 17915. Угол между прямой и плоскостью
П : Ax+By+Cz+D=0
П
ϕ
α