Слайд 1Численные методы
Преподаватель:
Редькина Белла Александровна
Слайд 4Элементы теории погрешностей
Слайд 5Источники погрешностей
Математическая модель
Исходные данные
Приближенный метод
Округления при вычислениях
При вычислениях погрешности накапливаются
Слайд 8Числа могут быть записаны с помощью конечного числа разрядов в
какой-либо системе счисления
a=±(a1bn+a2bn-1+…+ambn-m+1)
ai − целые положительные числа; a1>0 0≤ai
номер разряда в котором стоит цифра
n − старший разряд
n-m+1 − младший разряд
Слайд 9Пример:
Число a=435,7068 записать в виде позиционного разложения
Решение:
а=435,7068=4⋅102+3⋅101+5⋅100+7⋅10-1+
+0⋅10-2+6⋅10-3+8⋅10-4
Слайд 10
Использование приближенных чисел приводит к тому, что из множества действительных
чисел некоторого отрезка используется его конечное дискретное подмножество.
Количество разрядов в
записи числа ограничено.
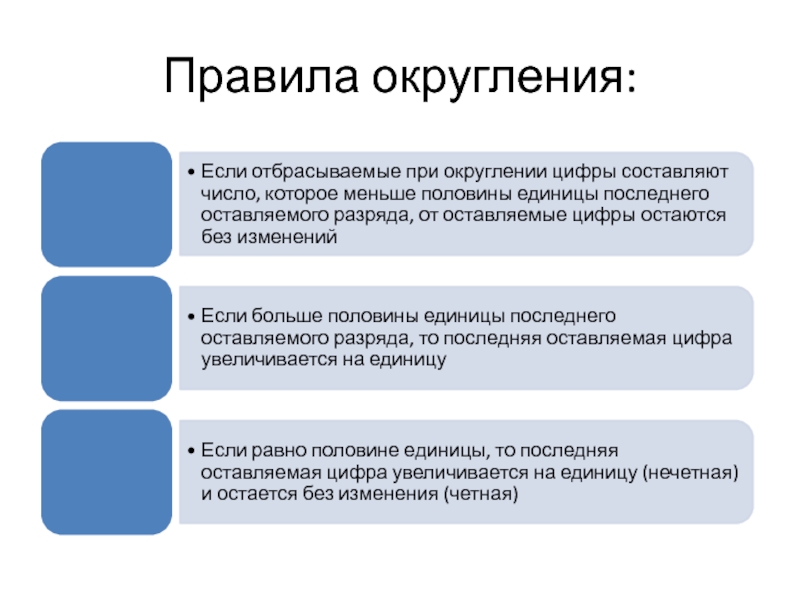
Слайд 11Округление
Использование числа с заданной степенью точности из конечного подмножества.
Округление применяют,
когда результаты вычислений содержат избыточное количество разрядов, по сравнению с
требуемой точностью.
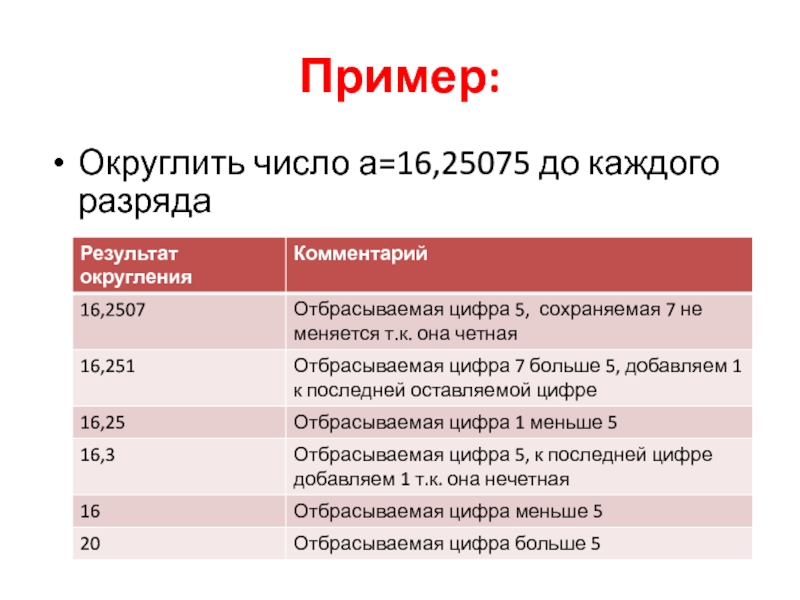
Слайд 13Пример:
Округлить число а=16,25075 до каждого разряда
Слайд 14Математические характеристики точности приближенных чисел
Слайд 16Предельная абсолютная погрешность
Слайд 17Истинная относительная погрешность
Слайд 18Предельная относительная погрешность
Слайд 19Пример
Выяснить, какое из приближенных равенств точнее:
Слайд 20Решение
Вычисляем значения:
Абсолютные погрешности:
Слайд 22Число верных знаков приближенного числа
Первая слева, отличная от нуля цифра
числа а, и все расположенные справа от нее цифры (в
том числе нули) называются значащими
Слайд 23Пример:
Выделить значащие цифры чисел:
а1=0,0273050
а2=2,7305
а3=0,0002730
Слайд 26Пример:
Известно, что в числе а=341,267 все цифры верные. Найти предельную
абсолютную и относительную погрешности.
Решение:
Слайд 27
При округлении и записи абсолютной и относительной погрешности пользуются правилами:
Погрешность
всегда округляют в большую сторону не пользуясь правилами округления.
Погрешность записывают
с двумя значащими цифрами.
Слайд 28Погрешность арифметических действий
Слайд 29При вычислении погрешности результата математических вычислений определить какое действие выполняется
последним:
Слайд 30Пример
Решение:
Последней операцией является сложение
Слайд 31Отдельно находим обе предельные абсолютные погрешности