Векторы

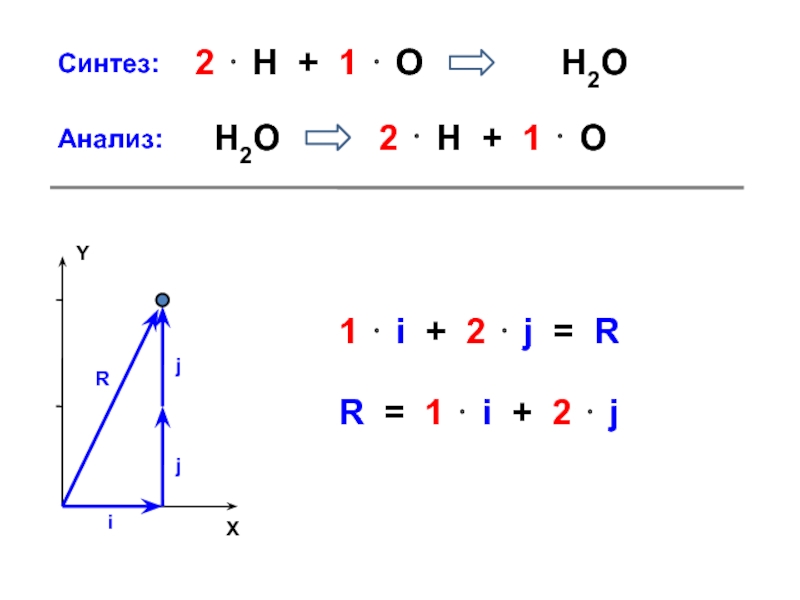
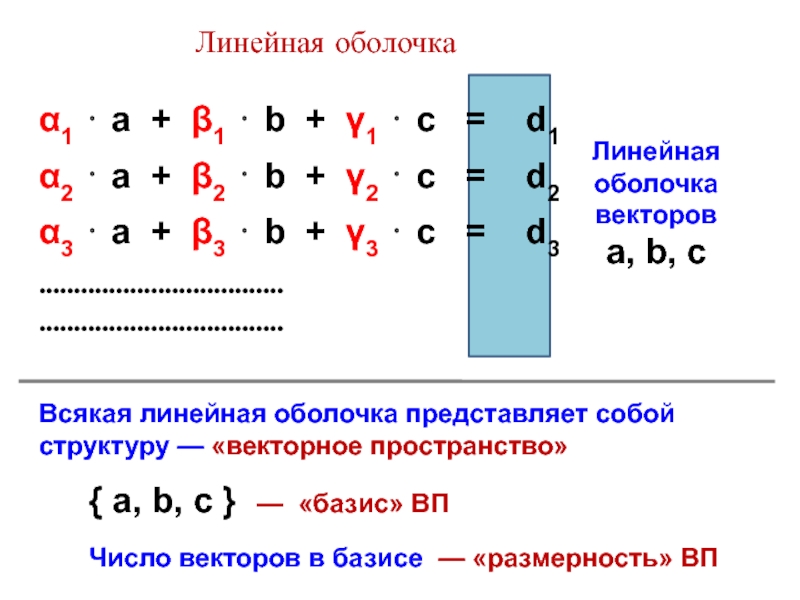
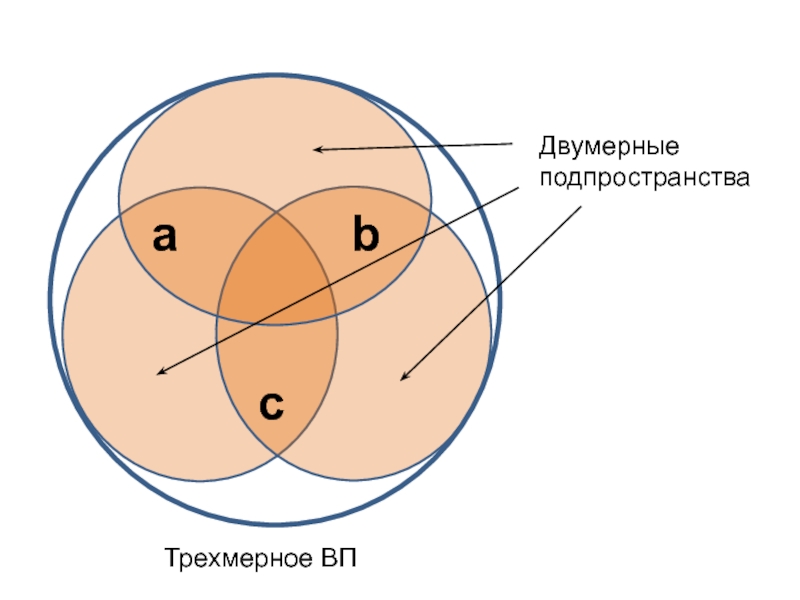
+ a = c
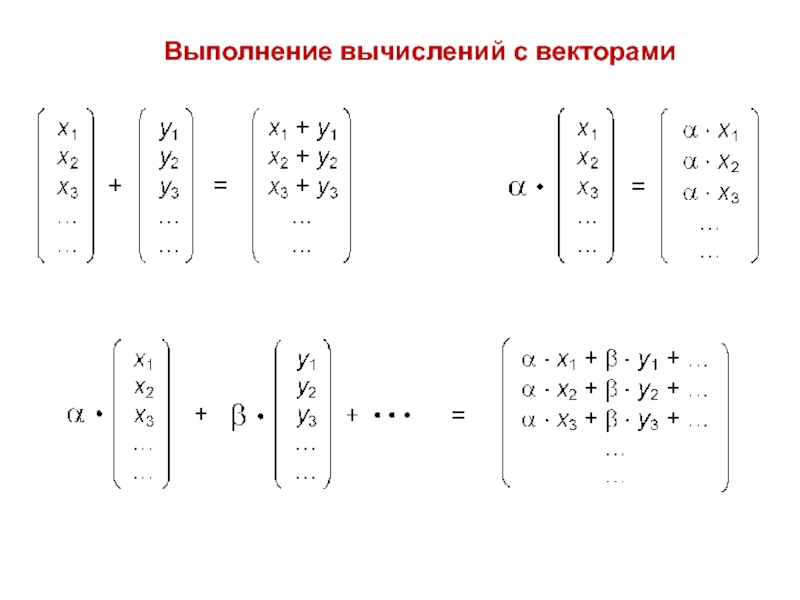
3. Вспомогательная операция «умножения на число»:

Правило: результат обеих операций — вектор, принадлежащий тому же множеству V , что и исходные векторы

α ⋅ b
(α + β) ⋅ a = α ⋅

Условия ассоциативности

α ⋅ a + β ⋅ b + γ ⋅ c + … = d

⋅ c = d1
Линейная оболочка векторов
a, b,

{ a, b, c } — «базис» ВП

Число векторов в базисе — «размерность» ВП

эквивалентных между собой базисов
(несмотря на то, что в такие

}
X = x1 ⋅ e1 + x2 ⋅ e2 +

Y = y1 ⋅ e1 + y2 ⋅ e2 + … + yn ⋅ en

Z = z1 ⋅ e1 + z2 ⋅ e2 + … + zn ⋅ en

••••••••••••••••••••••••••••••••••••••

X = ( x1, x2, … , xn )

Y = ( y1, y2, … , yn )

Z = ( z1, z2, … , zn )

Координатные представления векторов X, Y, Z относительно базиса { е1, е2, …, еn }

…, хn )
2. Всякий упорядоченный набор чисел ( х1, х2,

X = ( x1, x2, … , xn )

Вектор-строка
(ковариантный вектор)

Вектор-столбец
(контравариантный вектор)

S = α ⋅ R1 + β

x ⋅ y = 〈 x | y

Скалярное произведение
(число)

«свертка»

вектора Х
Нормировка векторов
X = ( x1, x2, … , xn

| X | ≠ 1

Нормированный вектор

Обычный (ненормированный) вектор

Скалярный квадрат

k ⋅ X }
где k — любое число, а

= 90o
ϕ = 180o
X ⋅ Y = 1
X ⋅ Y

X ⋅ Y = –1

Взаимная ориентация векторов

Y = (1 – 0)
X ⋅ Y = (0 –

Скалярное произведение — величина проекции одного из двух нормированных векторов на другой

S (см. задачу 2.2.) и исходными векторами (см. задачу 2.1.):
ϕ(S,

, xn ), где n = 1 000 000 000
X

Скалярное умножение