Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Функция y = log a x, её свойства и график
Содержание
- 1. 1 Функция y = log a x, её свойства и график
- 2. Свойства логарифма
- 3. ОпределениеЛогарифмической функцией называют функцию вида у=loga х, где х – переменная , a- число, a>0, a≠1.Определение
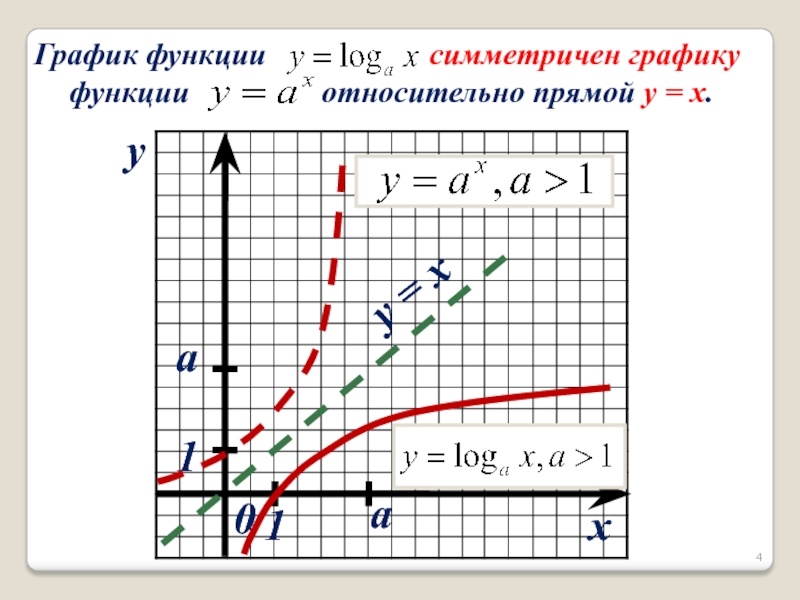
- 4. xy0aay = x11 График функции
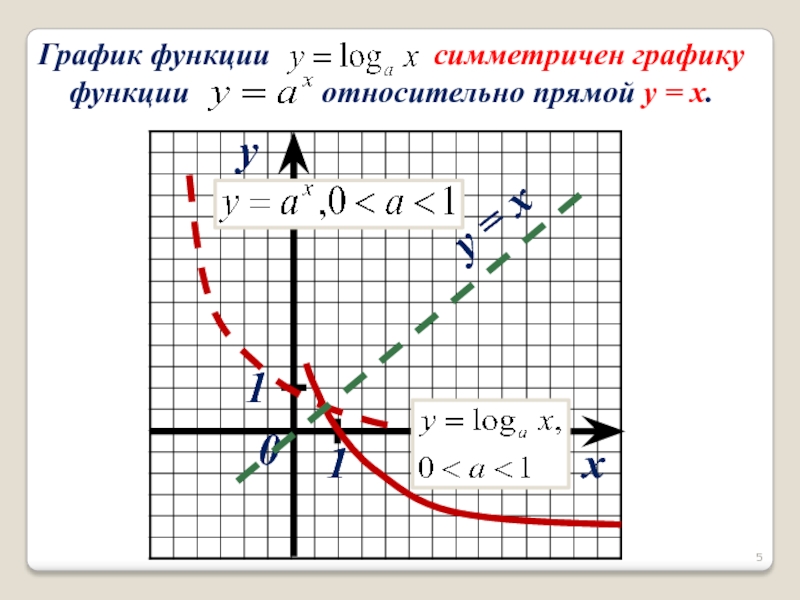
- 5. xyy = x110 График функции
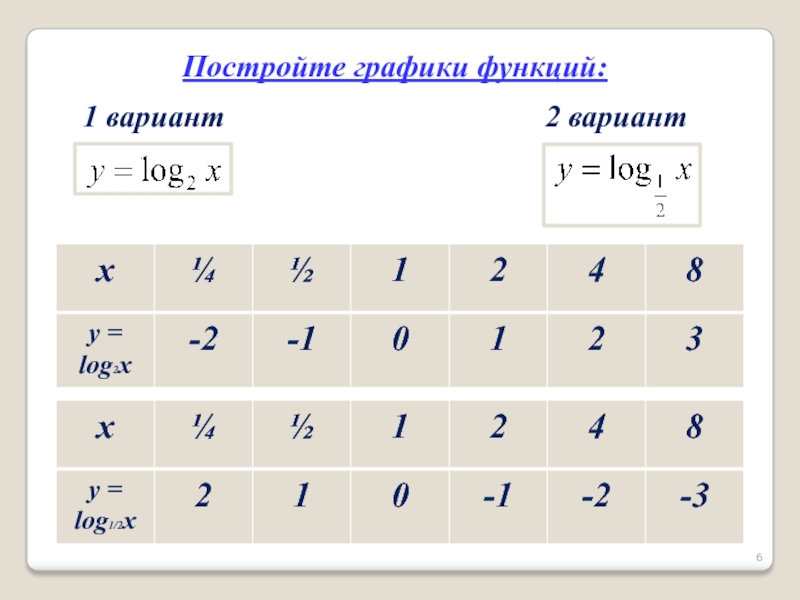
- 6. Постройте графики функций:1 вариант2 вариант
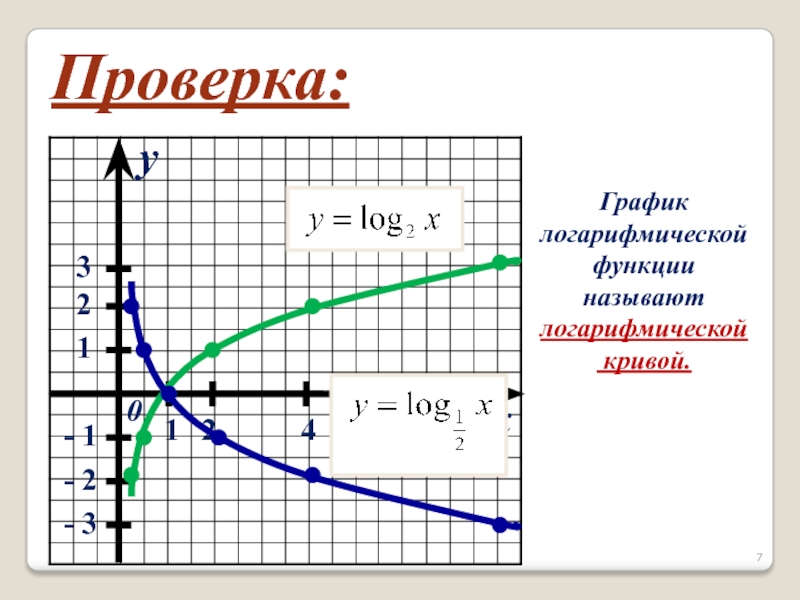
- 7. xy01231248- 1- 2- 3Проверка:График логарифмическойфункции называютлогарифмической кривой.
- 8. xy01231248- 1- 2График функции y = loga
- 9. 1) D(f) = (0, + ∞);2) не
- 10. 1) D(f) = (0, + ∞);2) не
- 11. Слайд 11
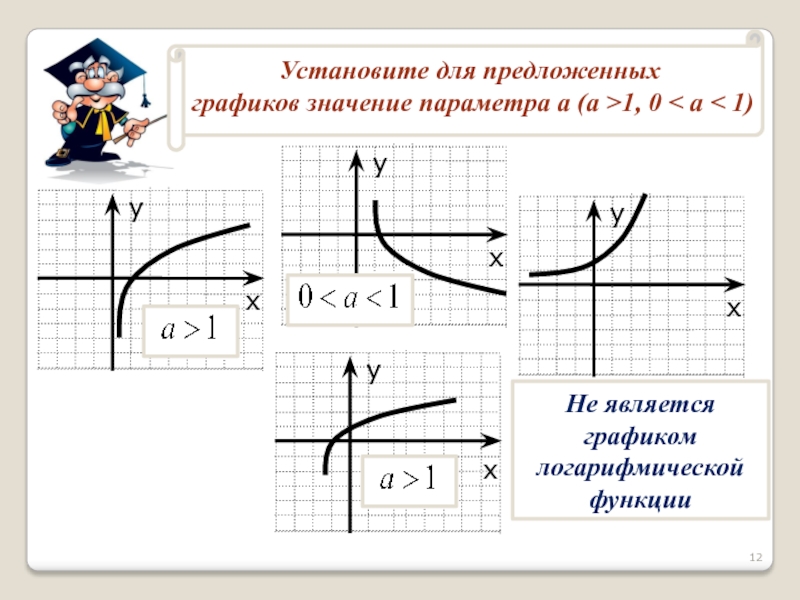
- 12. Не является графиком логарифмической функции
- 13. Задание 1. Найти
- 14. Решение: а) Функция
- 15. б) Функция
- 16. Слайд 16
- 17. Скачать презентанцию
Свойства логарифма
Слайды и текст этой презентации
Слайд 8x
y
0
1
2
3
1
2
4
8
- 1
- 2
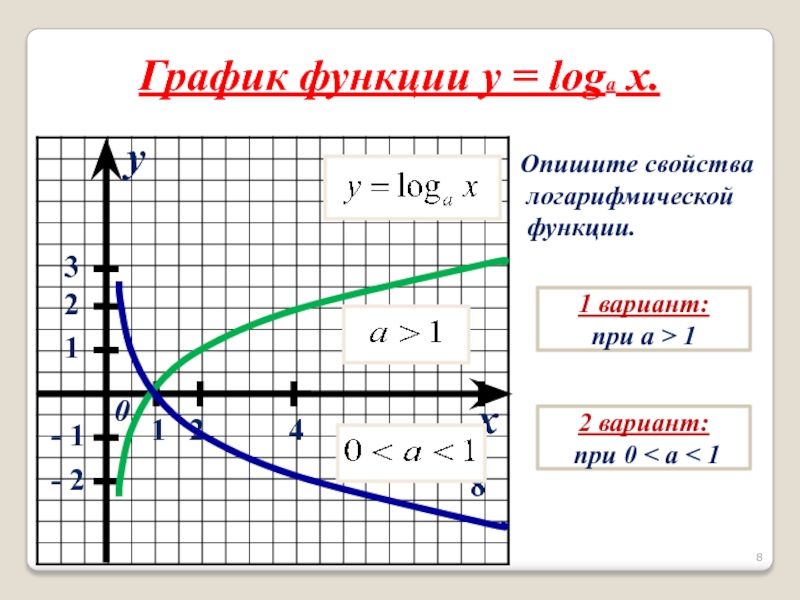
График функции y = loga x.
Опишите свойства
логарифмической
функции.
1 вариант:
при a > 1
2 вариант:
при
0 < a < 1Слайд 91) D(f) = (0, + ∞);
2) не является ни чётной,
ни нечётной;
3) возрастает на (0, + ∞);
4)не ограничена
сверху, не ограничена снизу; 5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
8) выпукла вверх.
Слайд 101) D(f) = (0, + ∞);
2) не является ни чётной,
ни нечётной;
3) убывает на (0, + ∞);
4)не ограничена
сверху, не ограничена снизу; 5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
8) выпукла вниз.