задачи двустороннюю обратимость, так что обратная к ней матрица всегда
единственна. В основе этого важнейшего свойства проматриц лежит введенное дополнительное регуляризирующее тождество.
Автономность, т.е. все уравнения (коэффициенты исходных уравнений) представлены в проматрице самостоятельными строками-уравнениями.
Разреженность, т.е. большое количество нулевых элементов проматрицы, что может значительно облегчить выполнение вычислительных процедур.
5. Универсальность – применимость для любой формы модели, т.е. в любой задаче исследуемую или синтезируемую систему можно представить в форме обобщенного уравнения и, следовательно, соответствующей проматрицы.
Свойства проматрицы



![1
Математическая модель линейной динамической системы в форме проблемных матриц Далее везде нумерация формул, определений и пр. дается в соответствии с [3]. Далее везде нумерация формул, определений и пр. дается в соответствии с [3].](/img/thumbs/eb9d8b596298659ce00ee13788aed199-800x.jpg)





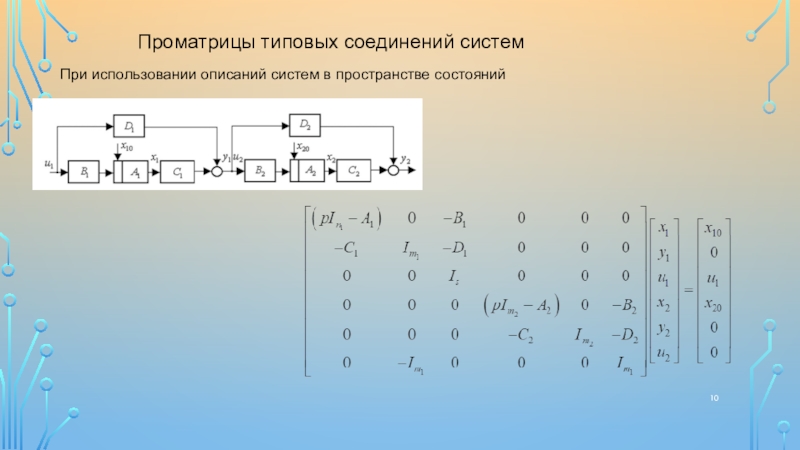
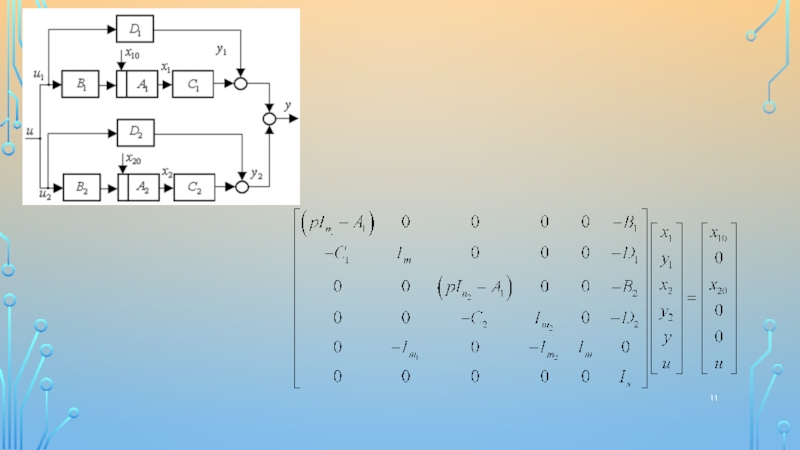
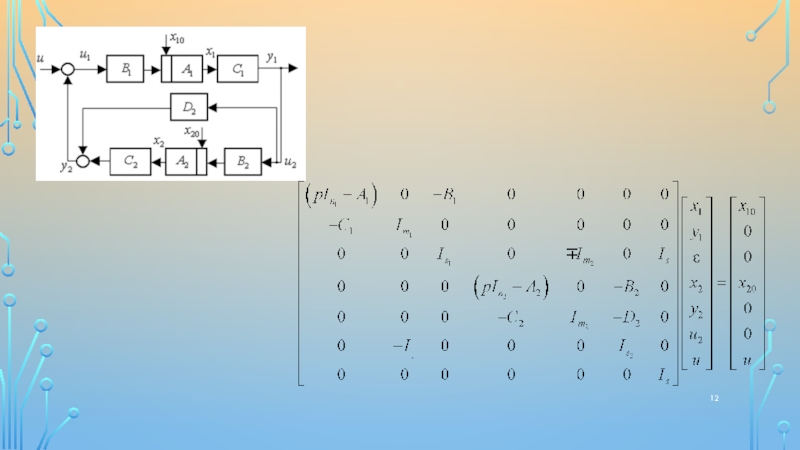
![1
Математическая модель линейной динамической системы в форме проблемных матриц Вопросы для самостоятельной проработкиОсновные законы управления, их синтез и свойства для Вопросы для самостоятельной проработкиОсновные законы управления, их синтез и свойства для SISO-объектов [4];Основные методы, математический аппарат для](/img/thumbs/aba7e241f201713d91f714b2661138ea-800x.jpg)