Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ До сих пор ничего не было сказано
Содержание
- 1. 1 ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ До сих пор ничего не было сказано
- 2. 2Для регрессии результаты линеаризованной модели имеют желаемые
- 3. 3Чтобы иметь возможность выполнять обычные тесты, он
- 4. 4В случае первого примера нелинейной модели проблем
- 5. 5При обсуждении логарифмической модели остаточный член полностью опускался.ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
- 6. 6ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХОднако неявно предполагалось, что в трансформированной модели имеется аддитивный остаточный член.
- 7. 7ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХЧтобы это было
- 8. 8ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХМы будем обозначать этот мультипликативный остаточный член как v.
- 9. 9ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХКогда u равно
- 10. 10ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХПоложительные значения u
- 11. vf(v)11Кроме того, чтобы удовлетворять условиям модели регрессии,
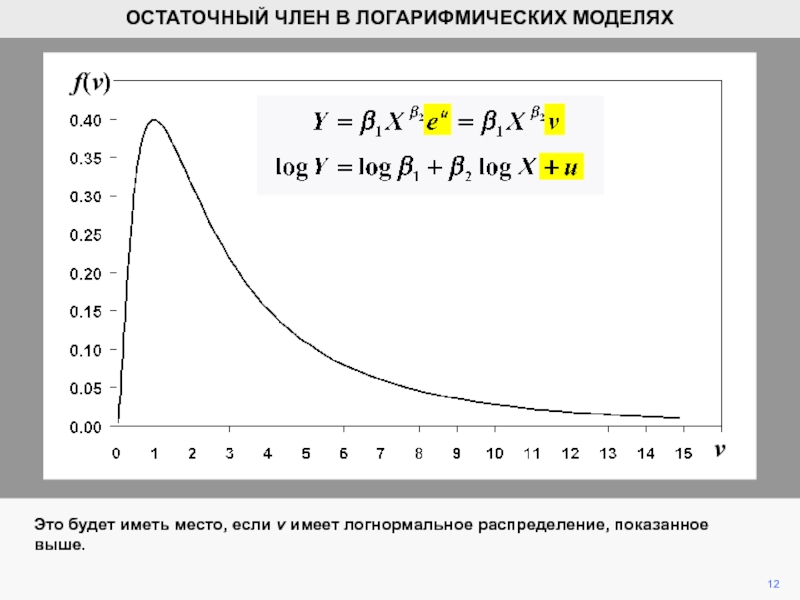
- 12. vf(v)12ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХЭто будет иметь место, если v имеет логнормальное распределение, показанное выше.
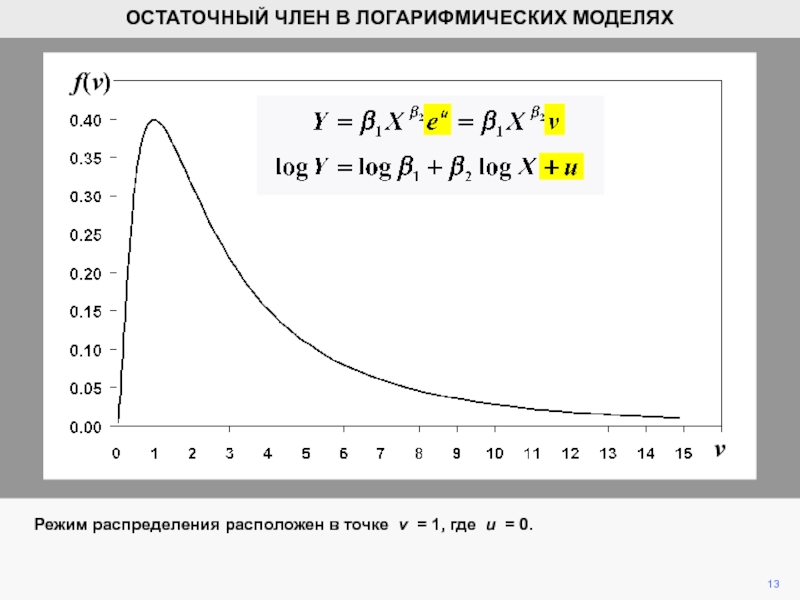
- 13. vf(v)13ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХРежим распределения расположен в точке v = 1, где u = 0.
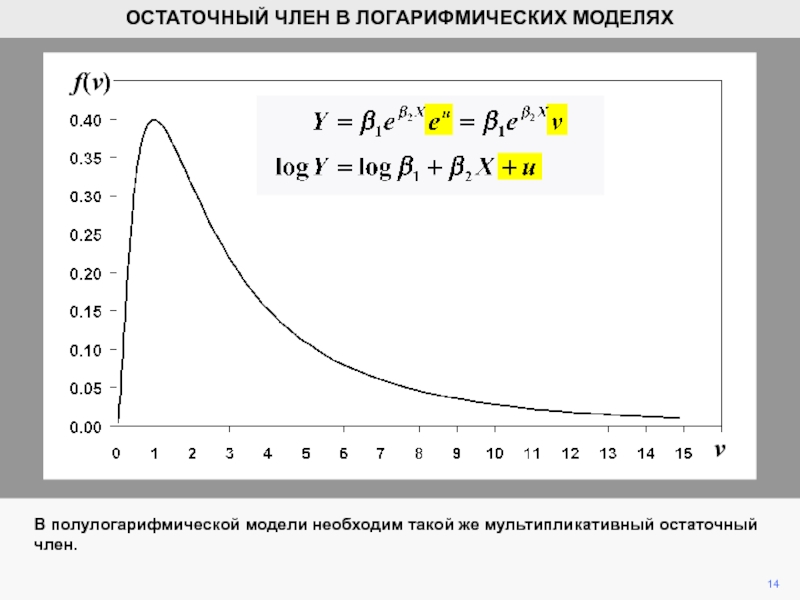
- 14. vf(v)14ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХВ полулогарифмической модели необходим такой же мультипликативный остаточный член.
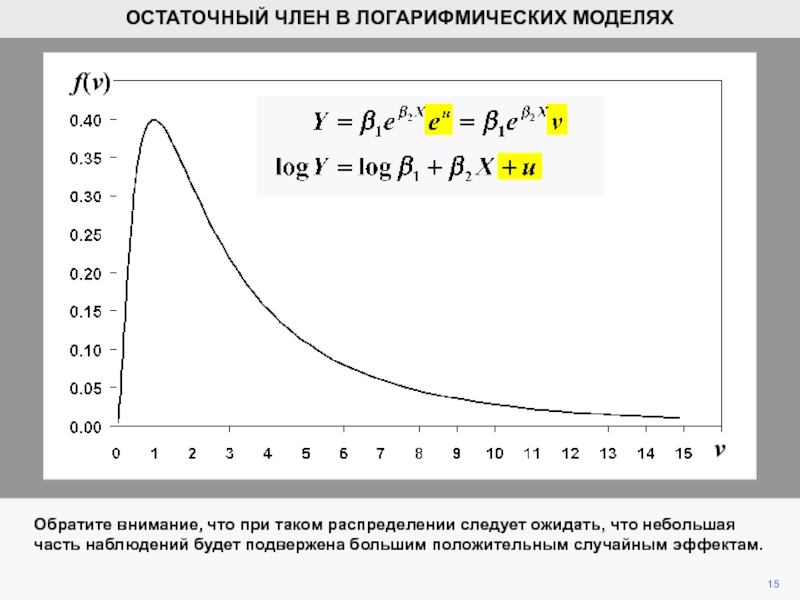
- 15. vf(v)15ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХОбратите внимание, что
- 16. 16Вот диаграмма разброса для заработка и обучения.
- 17. 17Вот диаграмма рассеяния для полулогарифмической модели с
- 18. 18Гистограмма выше сравнивает распределения остатков от линейных
- 19. 190–1–2–3123ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХМожно показать, что
- 20. 200–1–2–3123ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХОчевидно, что остатки
- 21. 21Что произойдет, если остаточный член в логарифмической
- 22. 22Если бы это было так, мы бы
- 23. Скачать презентанцию
2Для регрессии результаты линеаризованной модели имеют желаемые свойства, остаточный член в преобразованной модели должен быть аддитивным и должен удовлетворять условиям модели регрессии.ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Слайды и текст этой презентации
Слайд 11
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
До сих пор ничего не было
сказано об остаточном члене в моделях нелинейной регрессии.
Слайд 22
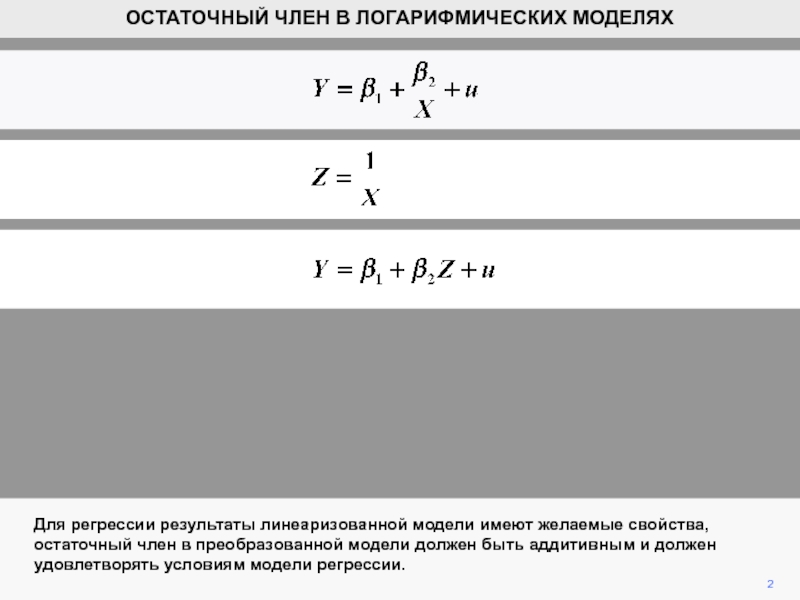
Для регрессии результаты линеаризованной модели имеют желаемые свойства, остаточный член
в преобразованной модели должен быть аддитивным и должен удовлетворять условиям
модели регрессии.ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Слайд 33
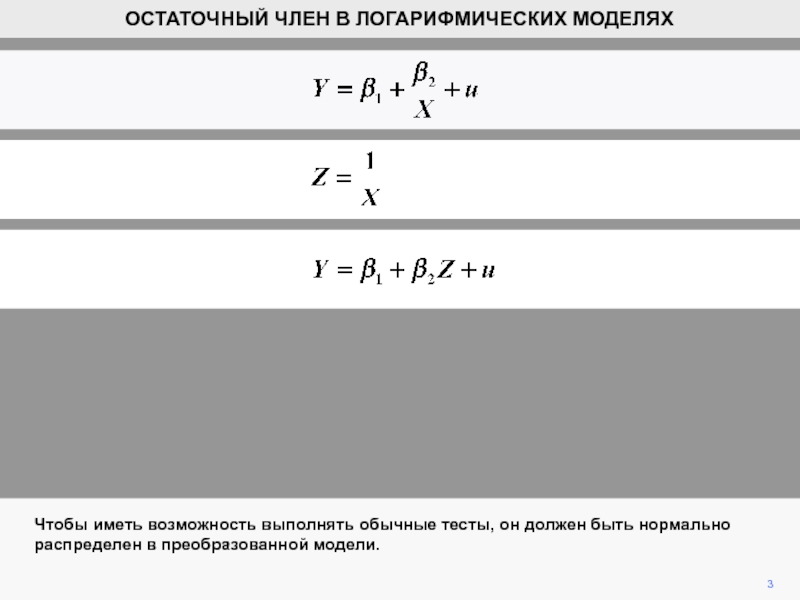
Чтобы иметь возможность выполнять обычные тесты, он должен быть нормально
распределен в преобразованной модели.
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Слайд 44
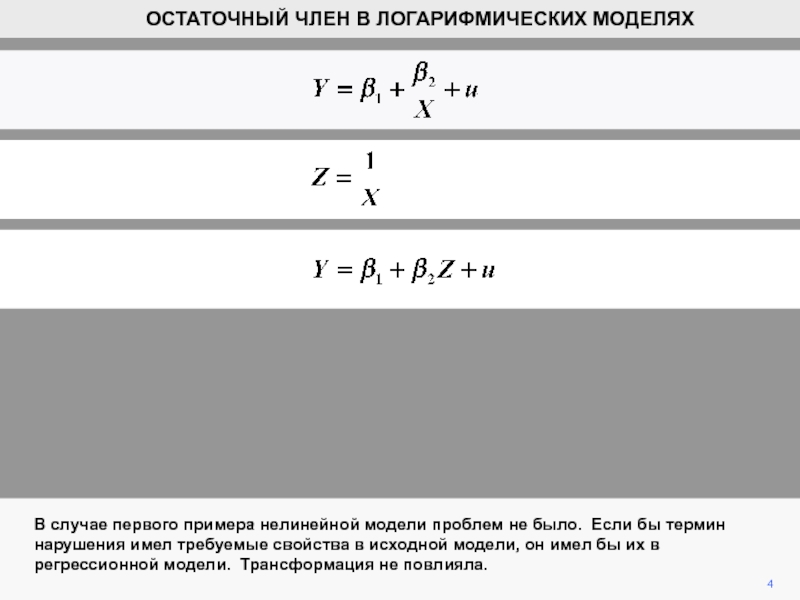
В случае первого примера нелинейной модели проблем не было. Если
бы термин нарушения имел требуемые свойства в исходной модели, он
имел бы их в регрессионной модели. Трансформация не повлияла.ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Слайд 55
При обсуждении логарифмической модели остаточный член полностью опускался.
ОСТАТОЧНЫЙ ЧЛЕН В
ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Слайд 66
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Однако неявно предполагалось, что в трансформированной
модели имеется аддитивный остаточный член.
Слайд 77
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Чтобы это было возможно, случайная составляющая
в исходной модели должна быть мультипликативным сроком eu.
Слайд 88
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Мы будем обозначать этот мультипликативный остаточный
член как v.
Слайд 99
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Когда u равно 0, не изменяя
значение log Y , v равно 1, также не изменяя
значение Y .
Слайд 1010
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Положительные значения u соответствуют значениям v
больше 1, случайный коэффициент положительно влияет на Y и log
Y. Аналогично отрицательные значения u соответствуют значениям v между 0 и 1, случайный фактор, оказывающий отрицательное влияние на Y и log Y
Слайд 11v
f(v)
11
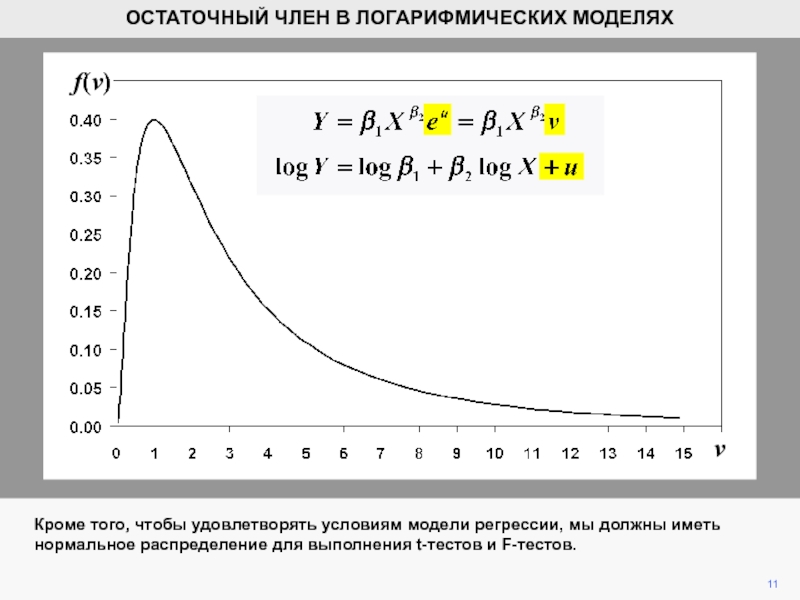
Кроме того, чтобы удовлетворять условиям модели регрессии, мы должны иметь
нормальное распределение для выполнения t-тестов и F-тестов.
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ
МОДЕЛЯХ
Слайд 12v
f(v)
12
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Это будет иметь место, если v
имеет логнормальное распределение, показанное выше.
Слайд 13v
f(v)
13
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Режим распределения расположен в точке v
= 1, где u = 0.
Слайд 14v
f(v)
14
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
В полулогарифмической модели необходим такой же
мультипликативный остаточный член.
Слайд 15v
f(v)
15
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Обратите внимание, что при таком распределении
следует ожидать, что небольшая часть наблюдений будет подвержена большим положительным
случайным эффектам.
Слайд 1616
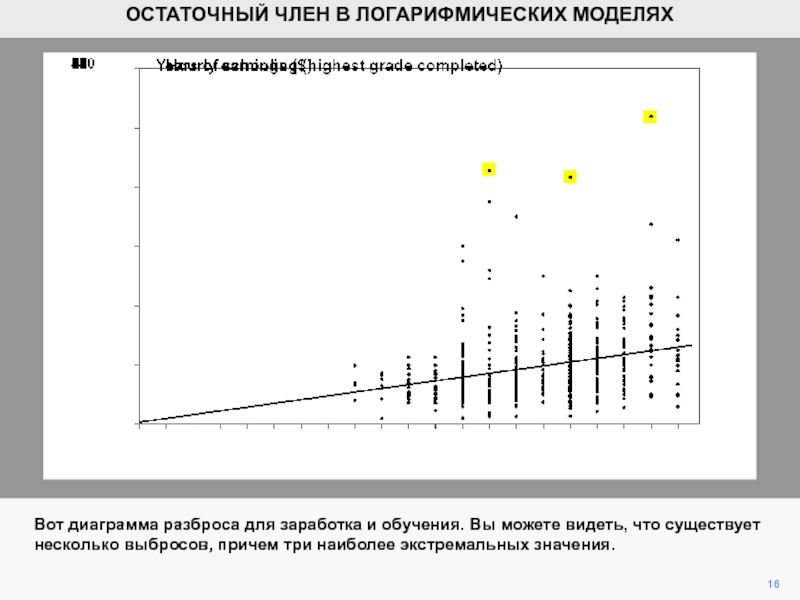
Вот диаграмма разброса для заработка и обучения. Вы можете видеть,
что существует несколько выбросов, причем три наиболее экстремальных значения.
ОСТАТОЧНЫЙ ЧЛЕН
В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Слайд 1717
Вот диаграмма рассеяния для полулогарифмической модели с ее регрессионной линией.
Те же три наблюдения остаются выбросами, но они не кажутся
настолько экстремальнымиОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Слайд 1818
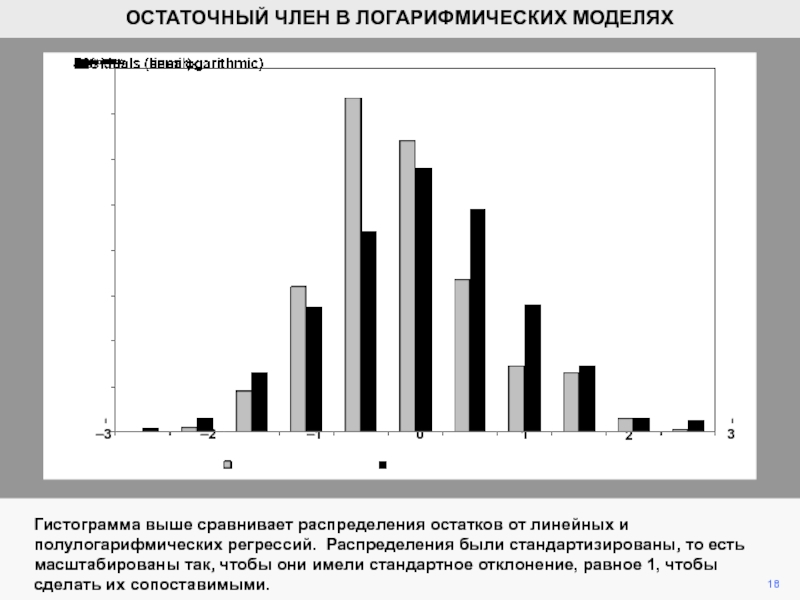
Гистограмма выше сравнивает распределения остатков от линейных и полулогарифмических регрессий.
Распределения были стандартизированы, то есть масштабированы так, чтобы они имели
стандартное отклонение, равное 1, чтобы сделать их сопоставимыми.0
–1
–2
–3
1
2
3
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Слайд 1919
0
–1
–2
–3
1
2
3
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
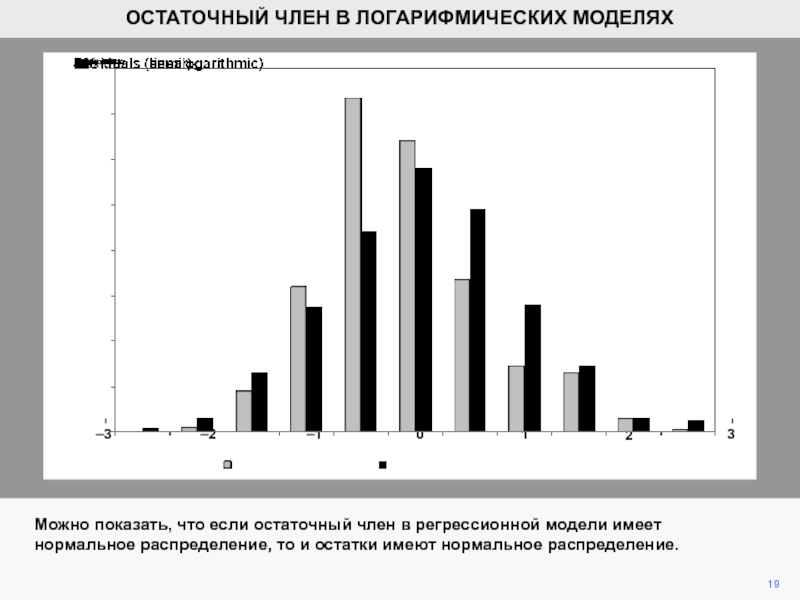
Можно показать, что если остаточный член
в регрессионной модели имеет нормальное распределение, то и остатки имеют
нормальное распределение.
Слайд 2020
0
–1
–2
–3
1
2
3
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Очевидно, что остатки от полулогарифмической регрессии
являются приблизительно нормальными, а остатки из линейной регрессии - нет.
Это свидетельствует о том, что полулогарифмическая модель является лучшей спецификацией.
Слайд 21
21
Что произойдет, если остаточный член в логарифмической или полулогарифмической модели
будет аддитивным, а не мультипликативным?
ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
Слайд 22
22
Если бы это было так, мы бы не смогли линеаризовать
модель, взяв логарифмы. Нет упрощения
Нам нужно будет использовать некоторую нелинейную регрессионную технику.ОСТАТОЧНЫЙ ЧЛЕН В ЛОГАРИФМИЧЕСКИХ МОДЕЛЯХ
