Слайд 1
Помехоустойчивое кодирование (ЕСС)
Блочные коды
Слайд 2 Основные характеристики кода
К числу основных характеристик кода относятся длина
кода n, его основание m, мощность кода N, вес кодовой
комбинации, кодовое расстояние
Основание кода m: код может быть двоичным, тогда m = 2, и недвоичным,
в этом случае m = 2n, n – целое
Вес кодовой комбинации (Hamming weight) w(U) – это число единиц
в кодовом слове для блоковых кодов
Мощность кода N — число разрешенных кодовых комбинаций
Для оценки отличия одной двоичной кодовой комбинации от другой используется расстояние Хэмминга d(v1, v2), определяемое как число разрядов, в которых одна кодовая комбинация v1 = (v10, v11, v12, v13, v14, … v1n) отличается от другой v2 = ( v20, v21, v22, v23, v24, … v2n).
Для характеристики обнаруживающей и исправляющей способности кода используют кодовое расстояние − это наименьшее расстояние Хэмминга для данного кода; обозначение dмин или dH(v1, v2)
Отношение R = k/n называют (относительной) скоростью кода
Слайд 3Основные характеристики кода
Слайд 4Блочные двоичные коды (n, k)
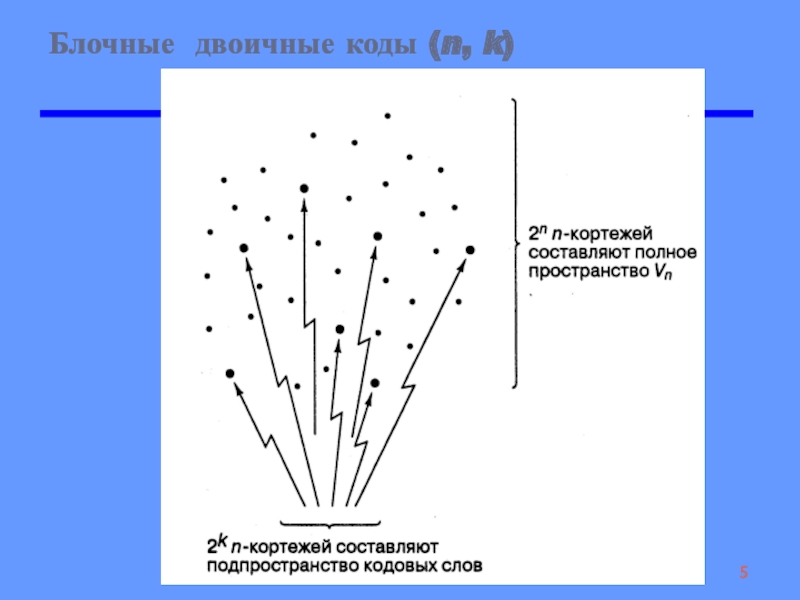
k информационных символов – 2k наборов
векторов (двоичное векторное пространство U2={0,1}k)
n двоичных символов – 2n
наборов векторов (двоичное векторное пространство U2={0,1}n)
из 2n наборов из U2={0,1}n выбираются 2k наборов векторов длиной n → векторное подпространство
Код – подпространство двоичного векторного пространства U2={0,1}n такое, что векторы (слова) этого подпространства максимально удалены одно от другого
Слайд 5Блочные двоичные коды (n, k)
Слайд 6Пример. Код с повторением
Информационные слова 0 или 1
Кодовые слова:
информационное
слово 0 кодируется 000
информационное слово 1 кодируется 111
Поскольку кодовые слова
отличаются в 3-х позициях, то расстояние Хемминга dH = 3
Для расчета dмин необходимо вычислить все 2k(2k – 1) расстояний между различными парами кодовых слов
Даже для сравнительно коротких кодов с k > 50 это практически невозможно
Важно: для линейных блоковых кодов при расчете dмин необходимо рассчитать веса Хемминга только для (2k – 1) ненулевых кодовых слов
Слайд 7Блоковые двоичные коды (n, k)
Линейный блоковый код — это такой
код, в котором вектор, не принадлежащий подпространству, нельзя получить путем
сложения любых кодовых слов, принадлежащих этому подпространству
Пусть Ui и Uj — два кодовых слова (или кодовых вектора) в двоичном блоковом коде (n, k).
Слайд 8
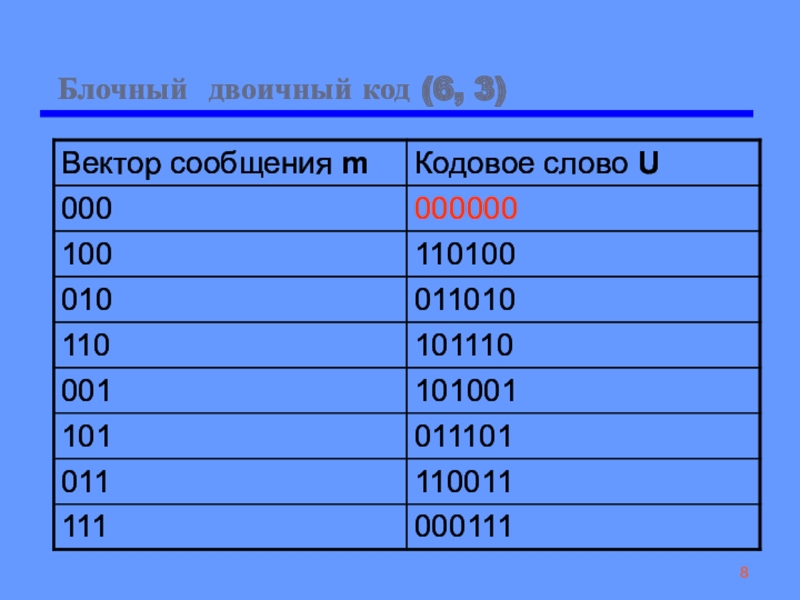
Блочный двоичный код (6, 3)
Слайд 9Вопрос студентам (письменно, №1)
Для заданного двоичного блочного кода (6, 3)
найдите вес каждого кодового слова
Слайд 10
Базис подпространства
Наименьшее линейно независимое множество, охватывающее подпространство (кодовых) слов,
называется базисом подпространства (V1, V2,..., Vk ), а число векторов
в этом базисном множестве является размерностью подпространства
U = m1 V1 + m2 V2 + … + mkV k
Слайд 11
Порождающая матрица G U = m
∙G
m = (m1, m2, …, mk ) U = (u1,
u2, …, un )
Слайд 13Упражнение для студентов (письменно, №2)
Порождающая матрица кода (6, 3)
Найдите кодовые
слова U1 и U2 для информационных слов m1 и m2
методом умножения U=m·G
а) m1 = (101)
б) m2 = (010)
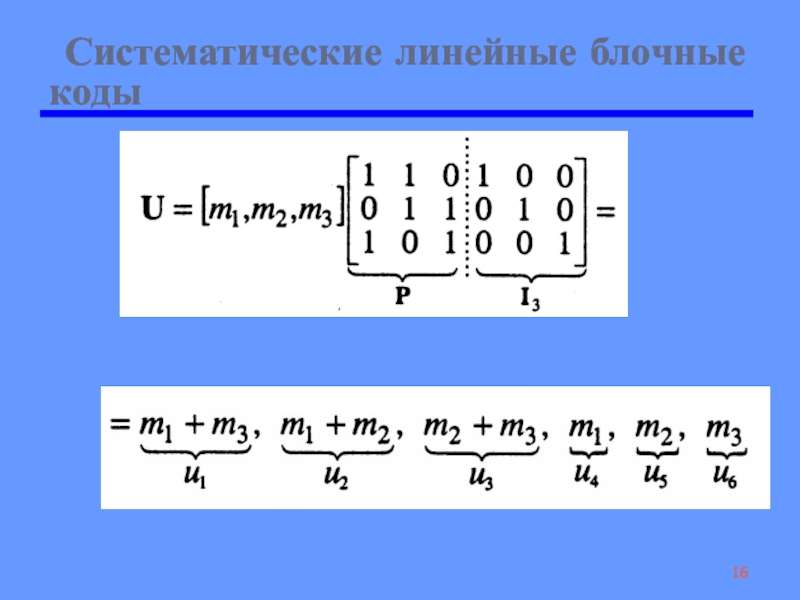
Слайд 14 Систематические линейные блочные коды
Слайд 15 Систематические линейные блочные коды
Слайд 16 Систематические линейные блочные коды
Слайд 19
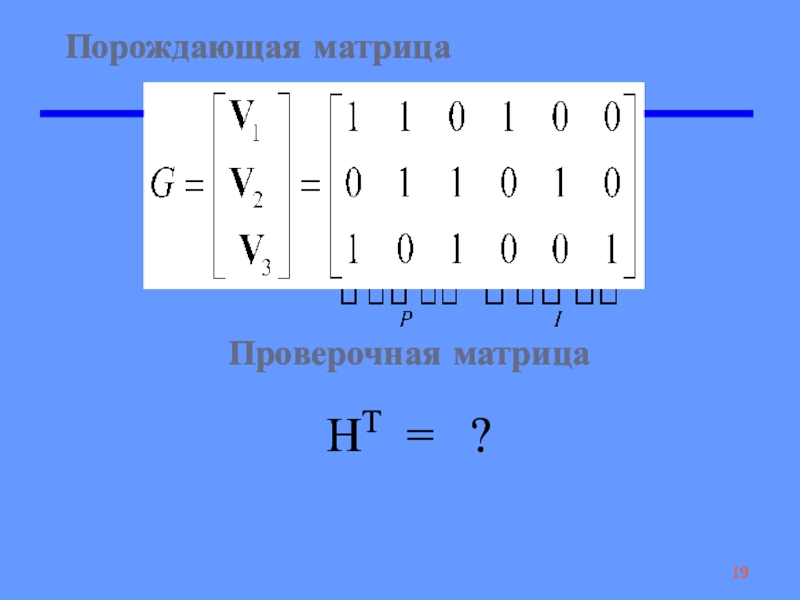
Порождающая матрица
Проверочная матрица
НT = ?
Слайд 20Упражнение для студентов (письменно, №3)
Решите задачу:
Рассмотрите линейный блочный код, проверочные
символы которого определяются из уравнений:
р1 = m1 + m2 +
m4
р2 = m1 + m3 + m4
р3 = m1 + m2 + m3
р4 = m2 + m3 + m4
Постройте порождающую и проверочную матрицы кода
Слайд 21Упражнение для студентов (письменно, №4)
Рассмотрен линейный блочный код, проверочные символы
которого определяются из уравнений:
р1 = m1 + m2 + m4
р2
= m1 + m3 + m4
р3 = m1 + m2 + m3
р4 = m2 + m3 + m4
Для этого кода построили порождающую и проверочную матрицы
Решите задачу:
Являются ли векторы [10101010] и [01011100] кодовыми словами?
Определите число исправимых ошибок при декодировании кода.
Слайд 22 Контроль с помощью синдромов (1)
r = r1, r2,
..., rп — принятый вектор U = и1, и2, ...,
иn — переданный вектор
r = U + е
е = е1, е2, ...,еn — вектор ошибки или ошибочная комбинация, внесенная каналом.
Всего в пространстве из 2n n-кортежей существует 2 n –1 возможных ненулевых ошибочных комбинаций.
Синдром сигнала r S = r Hт
Синдром — это результат проверки четности, выполняемой над сигналом r для определения его принадлежности заданному набору кодовых слов.
Если е = 0 синдром S = 0.
Верно ли: Если S = 0 ошибка е = 0 ???
Если r содержит ошибки, которые можно исправить, то синдром имеет определенное ненулевое значение, что позволяет отметить конкретную ошибочную комбинацию.
Декодер
ИЛИ производит прямое исправление ошибок локализует и исправляет ошибки (прямое исправление ошибок)
ИЛИ использует запрос ARQ посылает запрос на повторную передачу
Слайд 23 Контроль с помощью синдромов (2)
S =е Hт
Слайд 24 Контроль с помощью синдромов (3)
Контроль с помощью синдромов,
проведенный
над искаженным вектором кода или над ошибочной комбинацией, вызвавшей его
появление, даст один и тот же синдром.
Особенностью линейных блочных кодов, важной при декодировании, является
взаимно однозначное соответствие
между синдромом и
исправимой ошибочной комбинацией
Слайд 25 Контроль с помощью синдромов (4)
Пример. Блочный код (6,3)
Пусть
передано кодовое слово U = 1 0 1 1 1
0.
Принят вектор = 001110, (крайний левый бит принят с ошибкой).
Нужно найти вектор синдрома S = r Hт и показать, что он равен е Hт
Слайд 26 Контроль с помощью синдромов (5)
Решение
S = [1, 1+1, 1+1]
= [1 0 0]
(синдром искаженного вектора кода)
Проверим, что синдром искаженного
вектора кода равен синдрому ошибочной комбинации, которая вызвала эту ошибку
S = еНт = [1 0 0 0 0 0] Нт = [1 0 0]
(синдром ошибочной комбинации)
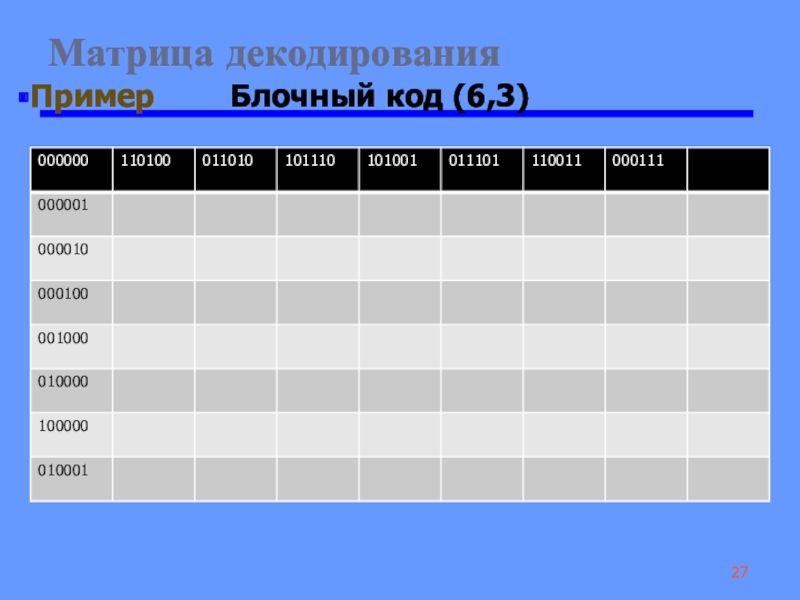
Слайд 27 Матрица декодирования
Пример Блочный код (6,3)
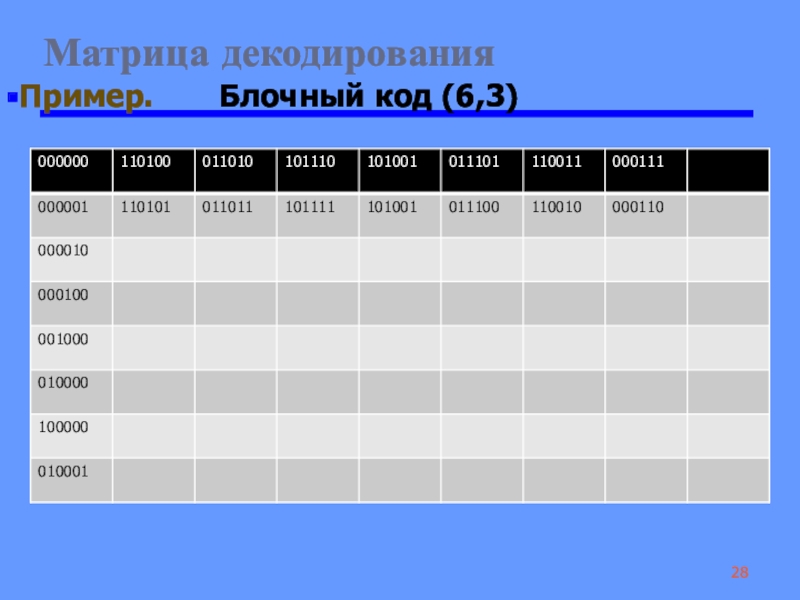
Слайд 28 Матрица декодирования
Пример. Блочный код (6,3)
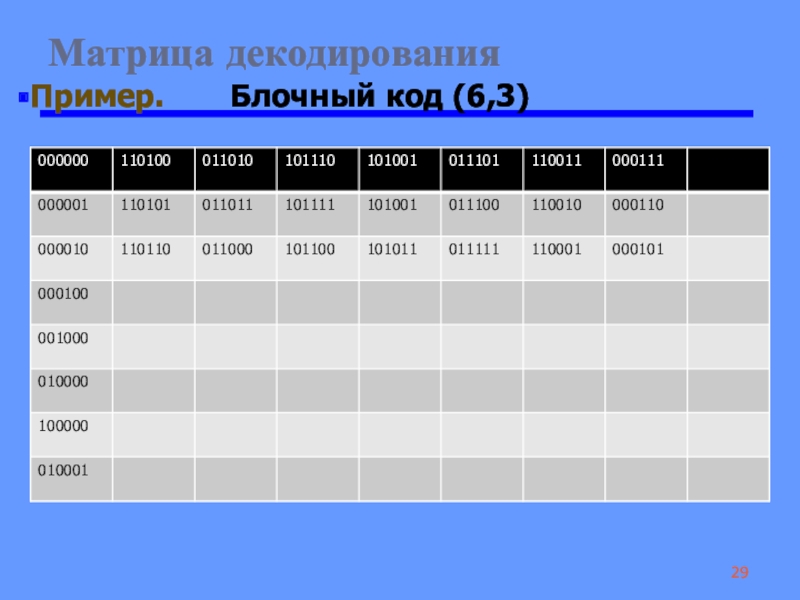
Слайд 29 Матрица декодирования
Пример. Блочный код (6,3)
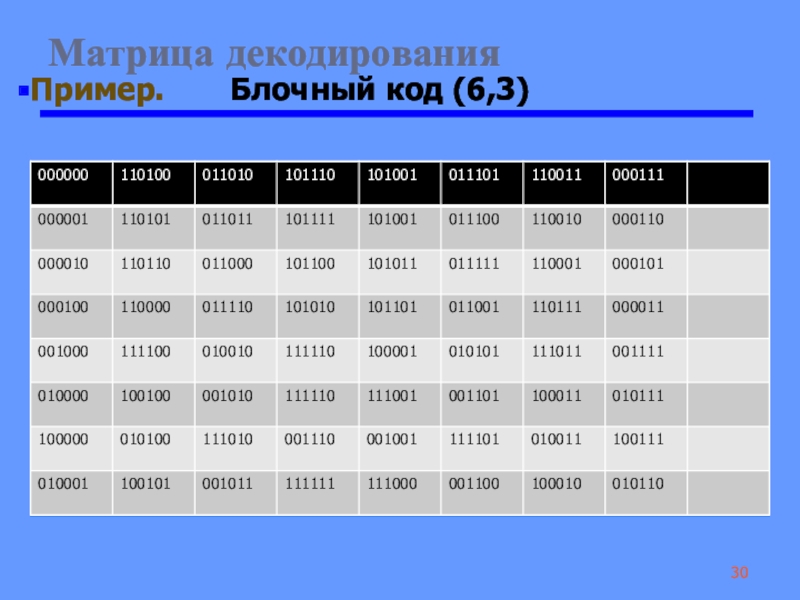
Слайд 30 Матрица декодирования
Пример. Блочный код (6,3)
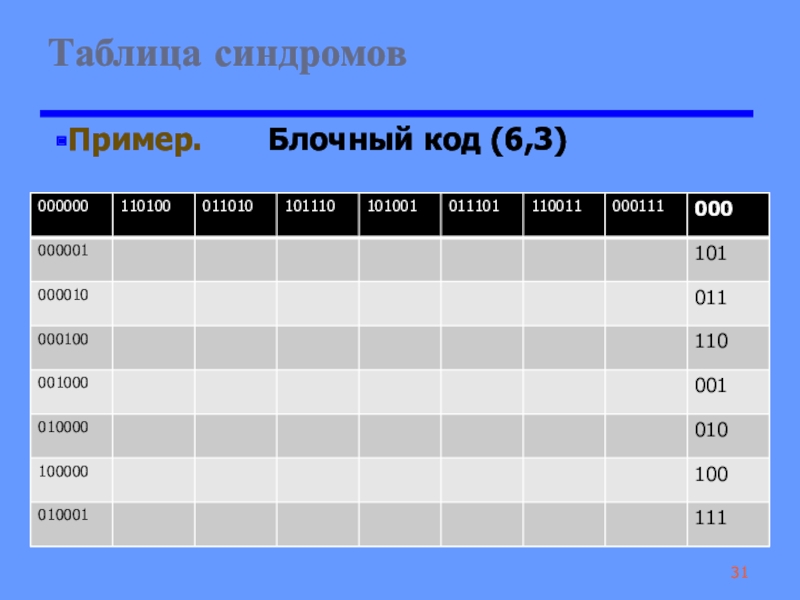
Слайд 31 Таблица синдромов
Пример. Блочный код (6,3)
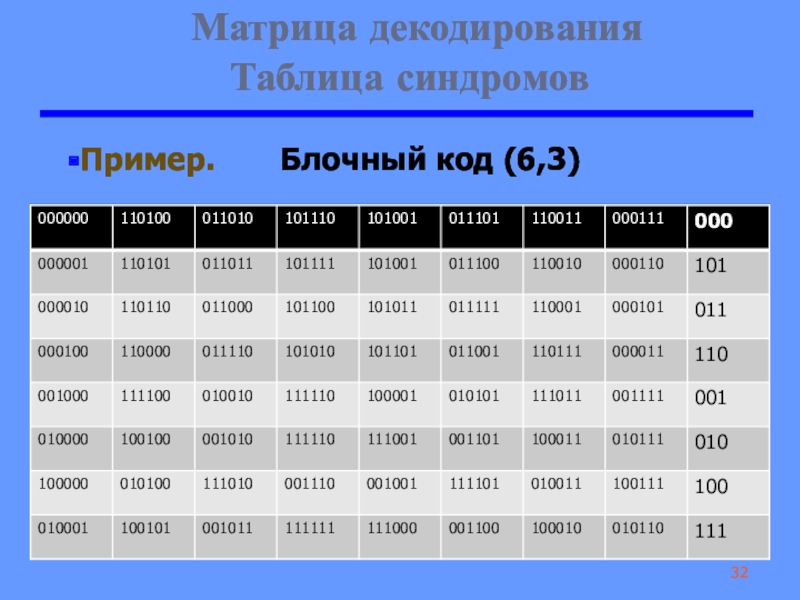
Слайд 32 Матрица декодирования
Таблица синдромов
Пример. Блочный код (6,3)
Слайд 33
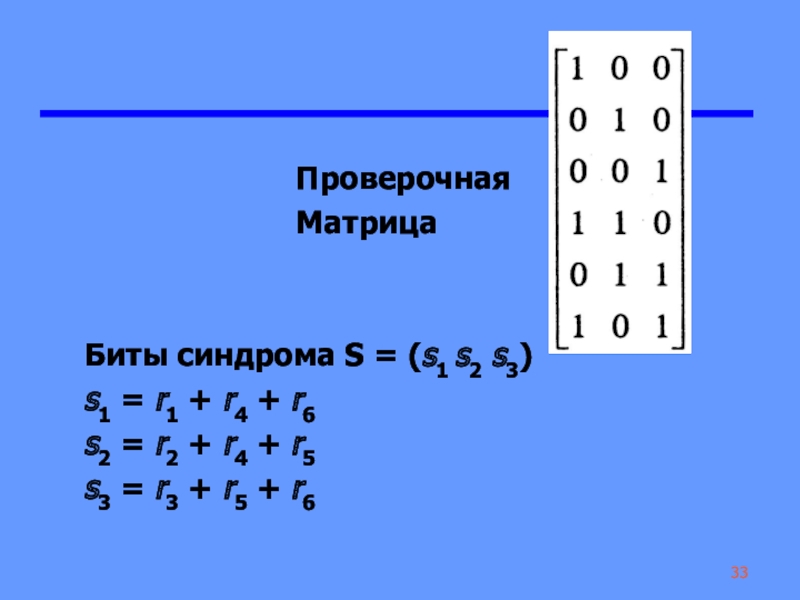
Проверочная
Матрица
Биты синдрома S = (s1 s2 s3)
s1 = r1
+ r4 + r6
s2 = r2 + r4 +
r5
s3 = r3 + r5 + r6
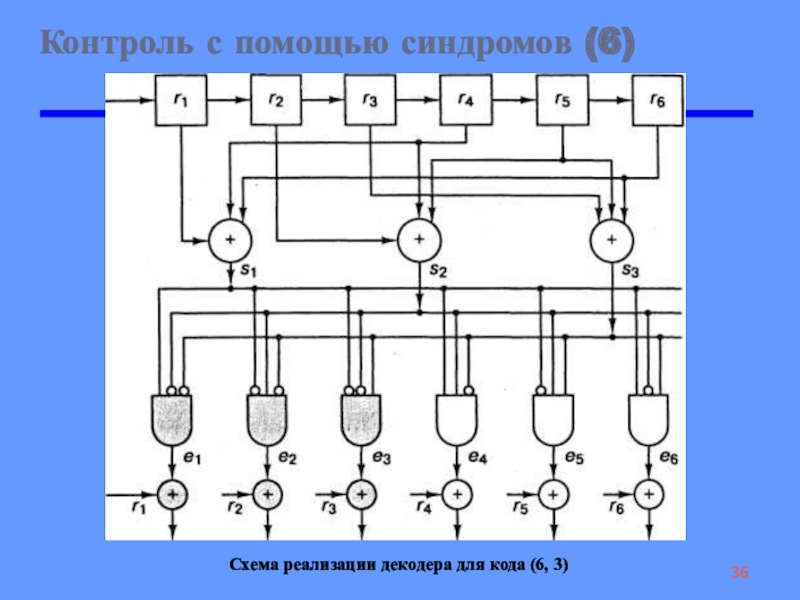
Слайд 34 Контроль с помощью синдромов (6)
Схема реализации декодера для кода
(6, 3)
Слайд 35Таблица синдромов
Пример Блочный код (6,3)
Слайд 36 Контроль с помощью синдромов (6)
Схема реализации декодера для кода
(6, 3)





















![1
Помехоустойчивое кодирование (ЕСС)
Блочные коды Контроль с помощью синдромов (5)РешениеS = [1, 1+1, 1+1] = Контроль с помощью синдромов (5)РешениеS = [1, 1+1, 1+1] = [1 0 0](синдром искаженного вектора кода)Проверим,](/img/tmb/6/586473/904a9ae37c4e782248a28afbd4c2f9d8-800x.jpg)