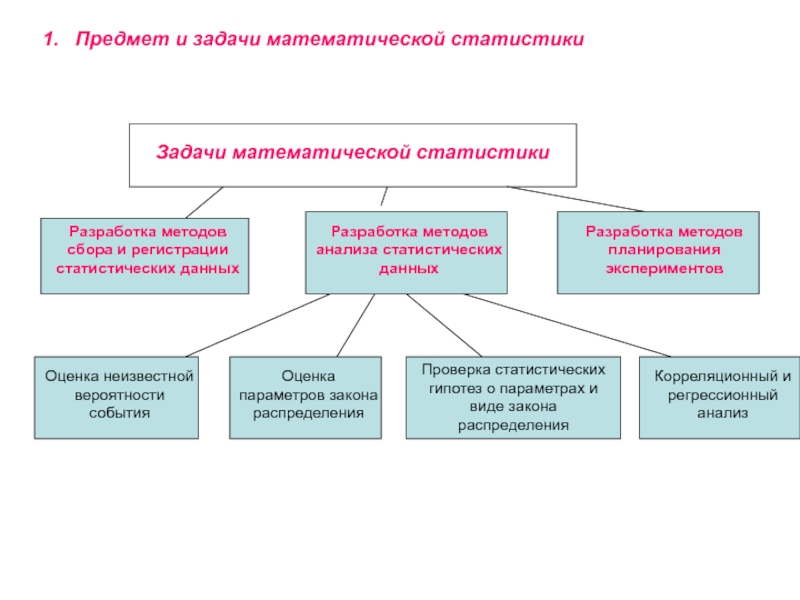
метод.
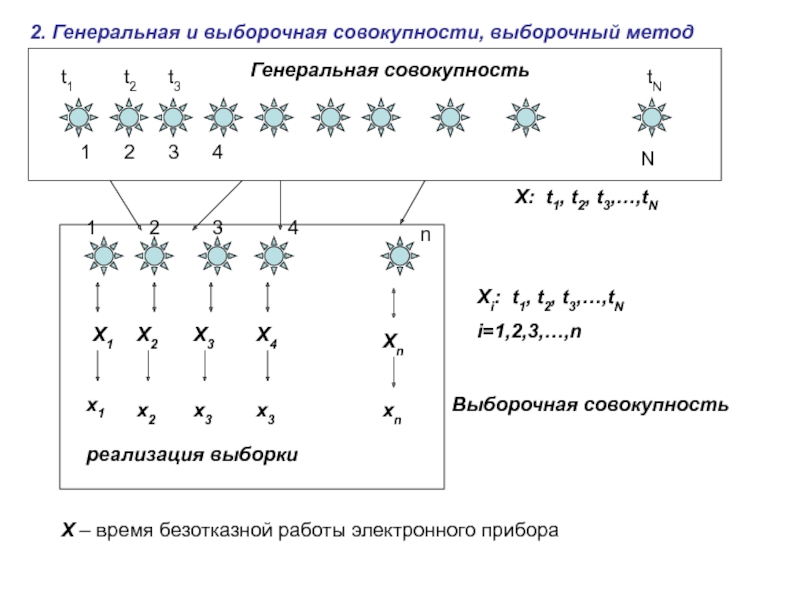
3.Вероятностная модель выборки.
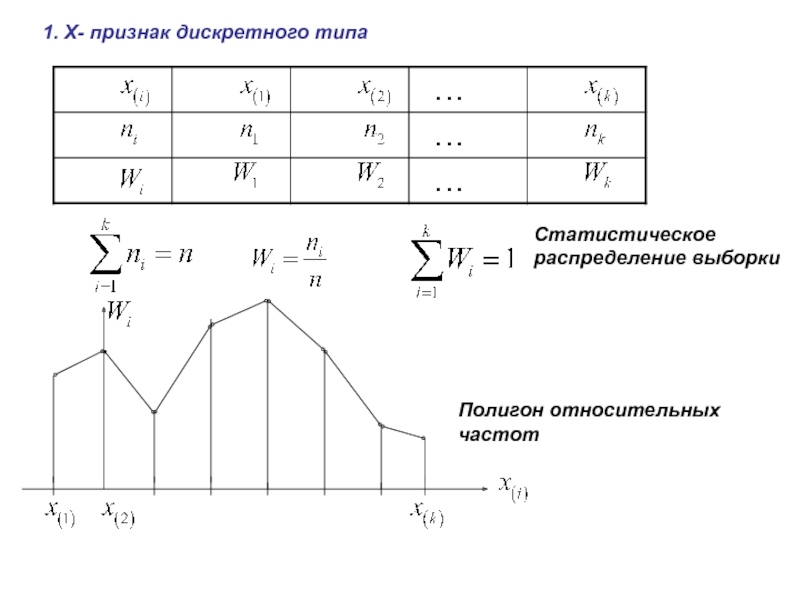
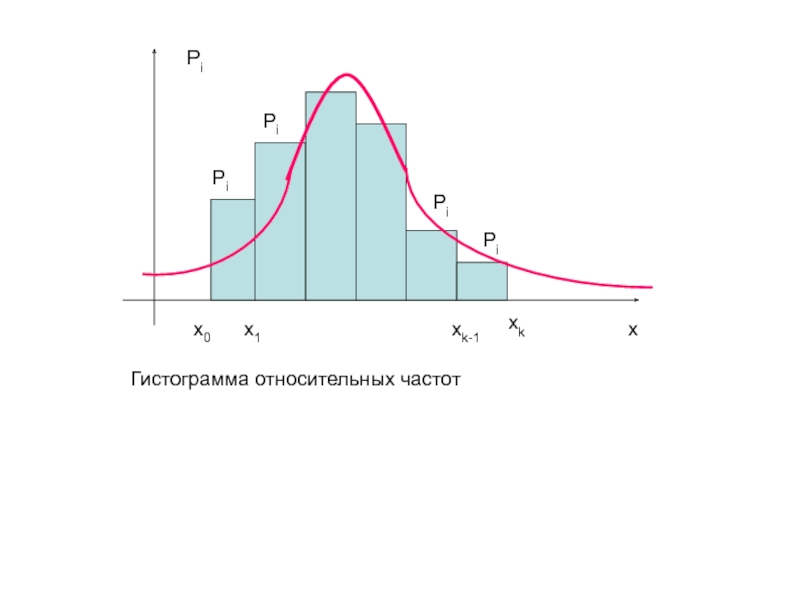
4. Статистическое распределение выборки. Полигон и гистограмма.
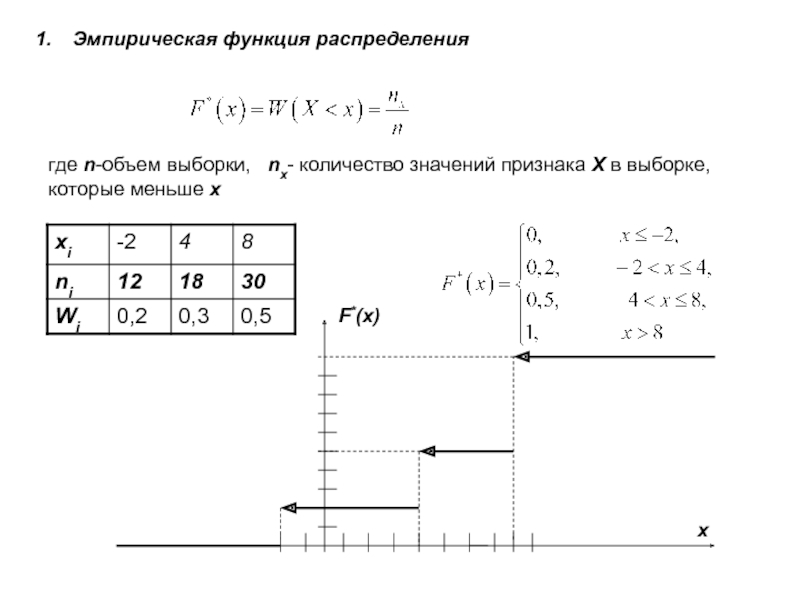
5.Эмпирическая функция
распределения.Лекция 1