Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
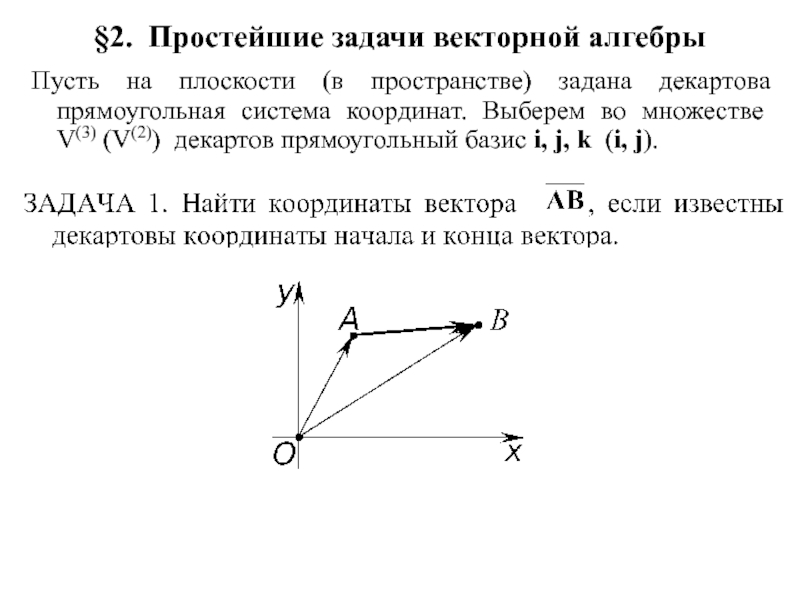
§2. Простейшие задачи векторной алгебры
Содержание
- 1. §2. Простейшие задачи векторной алгебры
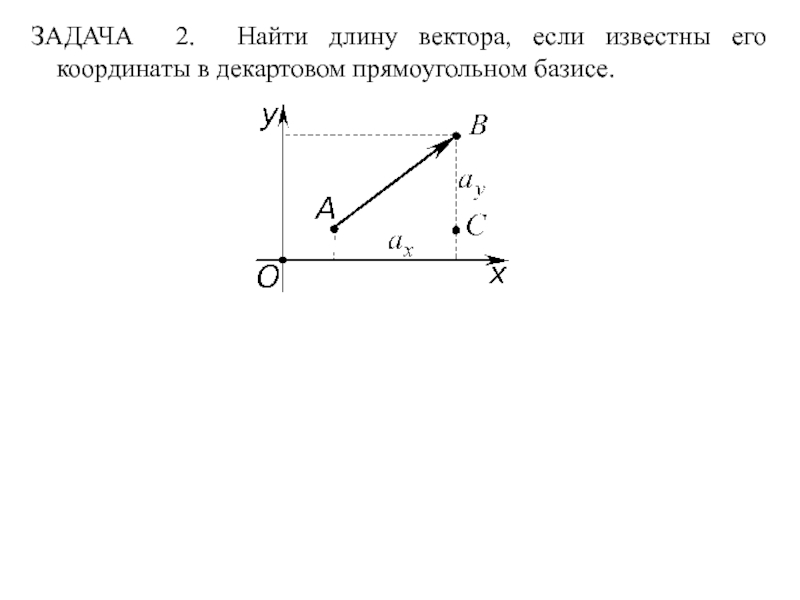
- 2. ЗАДАЧА 2. Найти длину вектора, если известны его координаты в декартовом прямоугольном базисе.
- 3. §3. Скалярное произведение векторовСВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ1) Скалярное произведение векторов коммутативно, т.е.
- 4. 2) Числовой множитель любого из двух векторов
- 5. 4) Скалярное произведение вектора на себя (скалярный
- 6. Скачать презентанцию
ЗАДАЧА 2. Найти длину вектора, если известны его координаты в декартовом прямоугольном базисе.