Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
2.1 Показатели безотказности объектов АО при нормальном распределении и
Содержание
- 1. 2.1 Показатели безотказности объектов АО при нормальном распределении и
- 2. При нормальном
- 3. Так как реальное время лежит в пределах 0
- 4. Нормирующий множитель q находится из условия равенства
- 5. 222*2][meqmM]} - интенсивность отказов
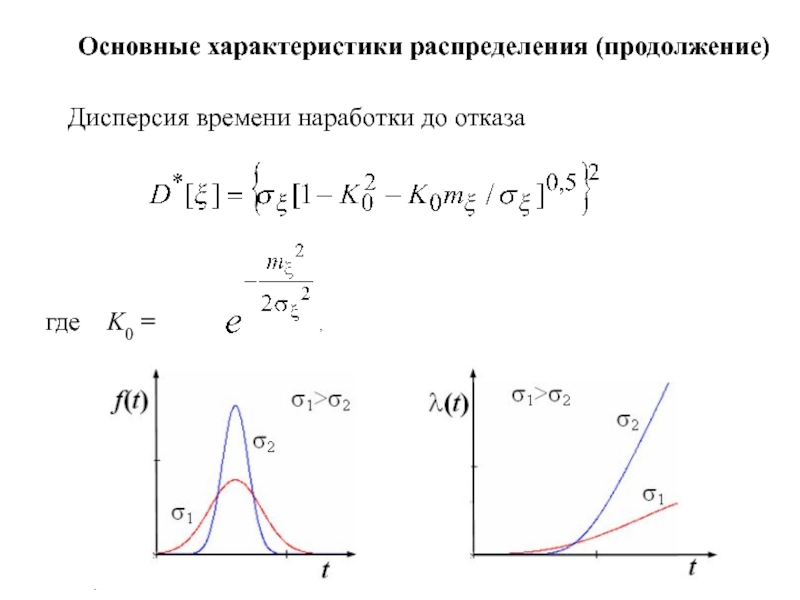
- 6. Основные характеристики
- 7. 2.2 Показатели безотказности объектов АО при экспоненциальном распределении
- 8. Случайная величина (СВ)
- 9. – дисперсия СВ :
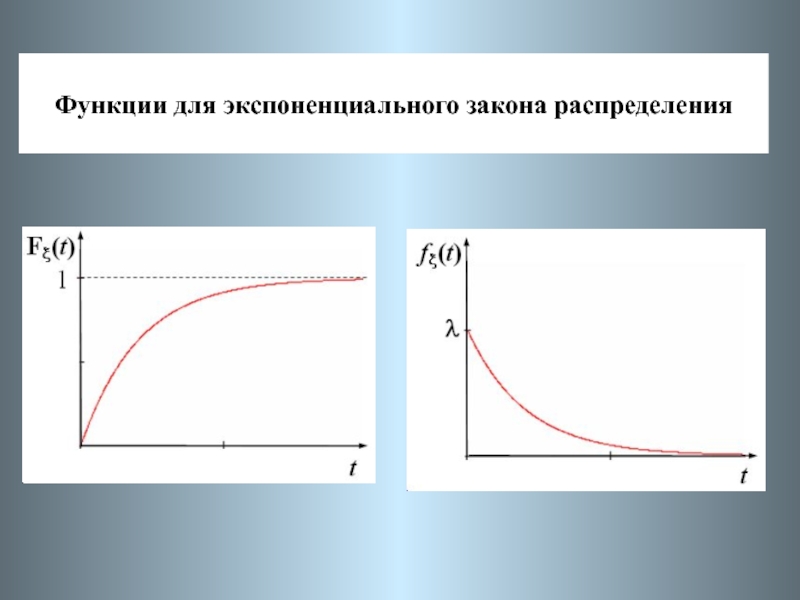
- 10. Функции для экспоненциального закона распределения
- 11. 2.3. Показатели безотказности объектов АО при равномерном распределении
- 12. Случайная величина
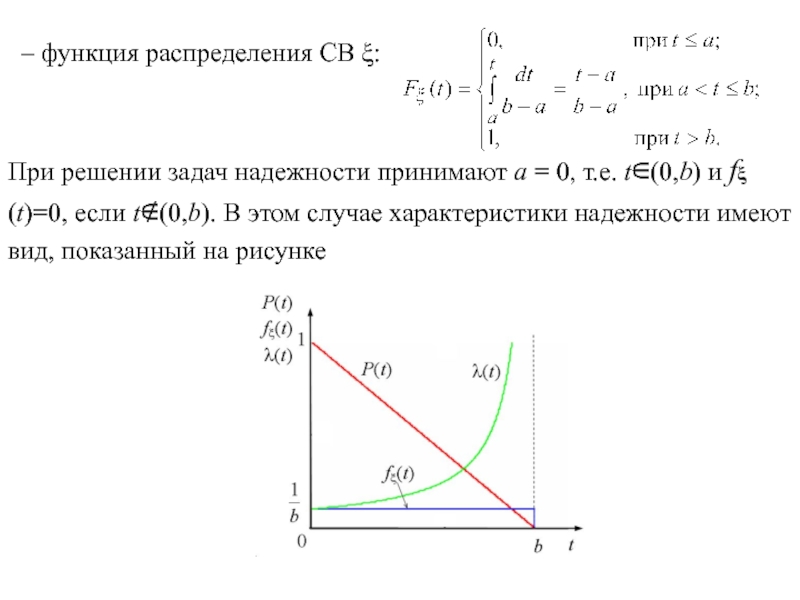
- 13. – функция распределения СВ :
- 14. - функция распределения
- 15. 2.4. Показатели безотказности объектов АО при распределении Вейбулла-Гнеденко
- 16. Случайная величина (СВ)
- 17. – среднее время безотказной работы:
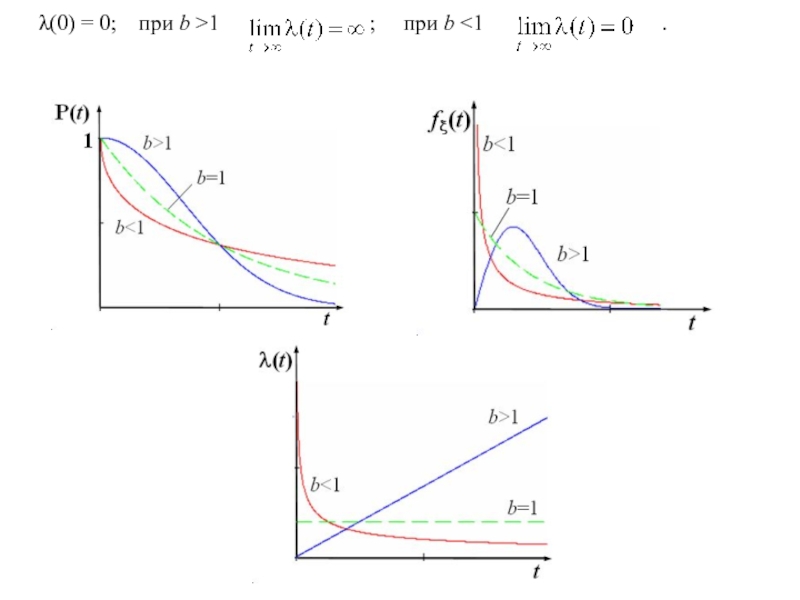
- 18. (0) = 0; при
- 19. 2.5 Показатели безотказности объектов АО при линейной интенсивности отказов
- 20. Случайная величина при
- 21. Проведем в (*) замену
- 22. Слайд 22
- 23. Скачать презентанцию
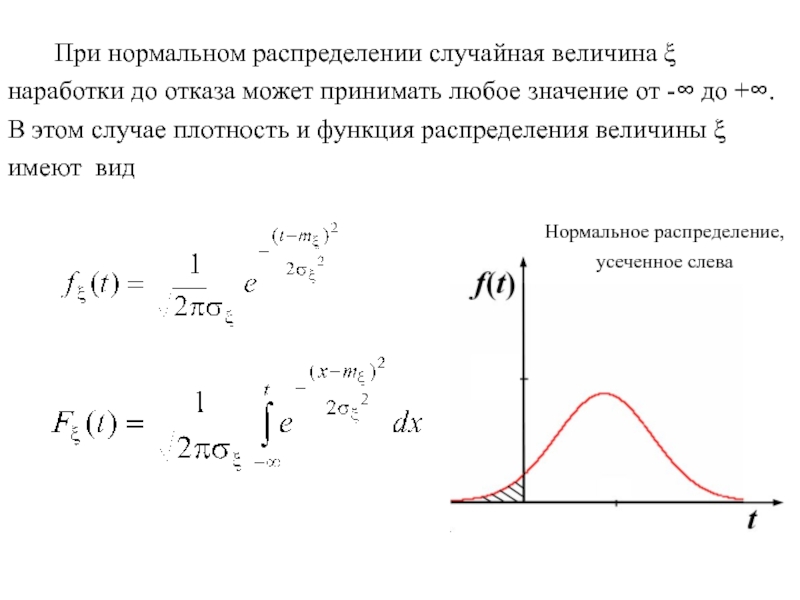
При нормальном распределении случайная величина наработки до отказа может принимать любое значение от - до +. В этом случае плотность и функция распределения величины
Слайды и текст этой презентации
Слайд 1
2.1 Показатели безотказности объектов АО при нормальном распределении и нормальном
распределении, усеченном слева
ОБЪЕКТА ДО ОТКАЗАСлайд 2 При нормальном распределении случайная величина
наработки до отказа может принимать любое значение от - до
+. В этом случае плотность и функция распределения величины имеют вид
Нормальное распределение,
усеченное слева
Слайд 3 Так как реальное время лежит в пределах 0
чтобы выполнялось условие
=1 . Если заштрихованная часть рисунка ничтожно мала (q0), то можно расчет характеристик надежности проводить, используя функцию распределения, заменяя нижний предел в интеграле на 0. Однако, если заштрихованная площадь под кривой f(t) является значительной, то ее необходимо учитывать. Для этого случая можно записатьСлайд 4Нормирующий множитель q находится из условия равенства единицы площади под
кривой . С учетом этого
после преобразований получимСлайд 52
2
2
*
2
]
[
m
e
q
m
M
]} - интенсивность отказов
-
математическое
ожидание наработки до отказа
/
)
[(
5
.
0
/{
2
1
)
(
)
(
)
(
2
2
2
)
(
*
m
t
e
t
P
t
f
t
m
t
Слайд 6 Основные характеристики распределения (продолжение)
,
Дисперсия времени наработки до отказа
где K0 =
Слайд 8 Случайная величина (СВ) называется экспоненциально распределенной
с параметром , если ее функция распределения имеет вид Распределение имеет
следующие характеристики: – вероятность безотказной работы – плотность вероятности распределения СВ – математическое ожидание СВ :, t 0, > 0.
Слайд 9 – дисперсия СВ : - СКО – интенсивность отказов
Свойство экспоненциального закона распределения: вероятность безотказной
работы на интервале (t, t +t) не зависит от времени предшествующей работы t, а зависит только от t:Слайд 12 Случайная величина (СВ) называется равномерно
распределенной, если ее плотность распределения внутри интервала (a, b) постоянна
и равна нулю вне этого интервала. Характеристики распределения : – плотность распределения СВ Слайд 13 – функция распределения СВ : При решении задач надежности принимают
а = 0, т.е. t(0,b) и f(t)=0, если t(0,b). В
этом случае характеристики надежности имеют вид, показанный на рисункеСлайд 14 - функция распределения и вероятность безотказной работы - математическое ожидание
и дисперсия - интенсивность отказов Равномерный закон распределения используется при
моделировании надежности при априорной неопределенности параметров.Слайд 16 Случайная величина (СВ) распределена по закону
Вейбулла-Гнеденко, если ее функция распределения имеет вид
, a>0 , b>0. При b=1 распределение является экспоненциальным с параметром =1/а. Характеристики распределения: – вероятность безотказной работы: – плотность вероятности: – интенсивность отказов:Слайд 17 – среднее время безотказной работы:
, где – гамма-функция от параметра находится по таблице. - дисперсия времени наработки до отказа Областью применения распределения Вейбулла-Гнеденко являются стареющие объекты: гироскопические приборы, электродвигатели и некоторые типы полупроводниковых приборов.
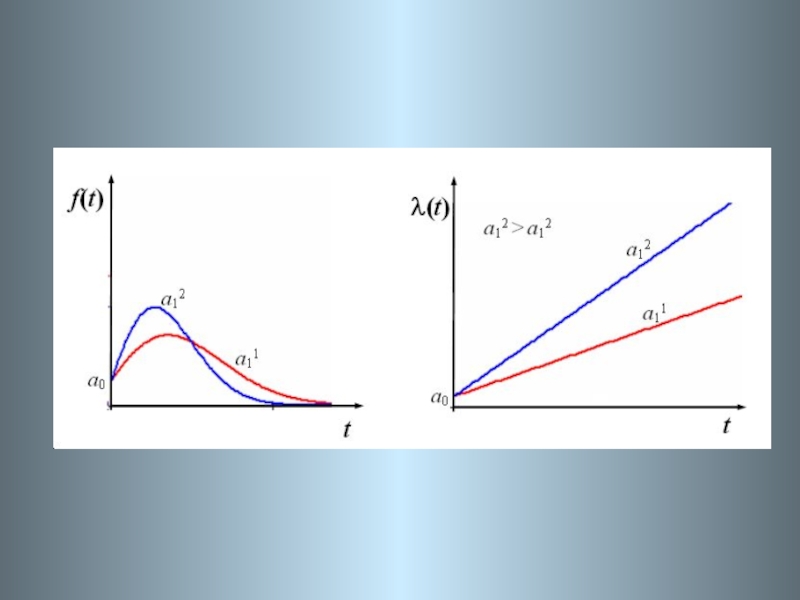
Слайд 20 Случайная величина при линейной интенсивности отказов
(t)=а0+а1t имеет следующие характеристики:
– функция распределения
- вероятность безотказной работы
– плотность распределения времени безотказной работы
– средняя наработка до первого отказа
(*)
Слайд 21 Проведем в (*) замену переменных
Тогда выражение
(*) можно преобразовать к виду
==
Используя таблицы для нормальной функции распределения, рассчитывается средняя наработка объекта до отказа.



![2.1 Показатели безотказности объектов АО при нормальном распределении и 222*2][meqmM]} - интенсивность отказов - математическое ожидание наработки до отказа /)[(5.0/{ 21)()()(222)(*mtetPtftmt 222*2][meqmM]} - интенсивность отказов - математическое ожидание наработки до отказа /)[(5.0/{](/img/thumbs/11696ea71521cc9e900924fa7bcbbc8c-800x.jpg)