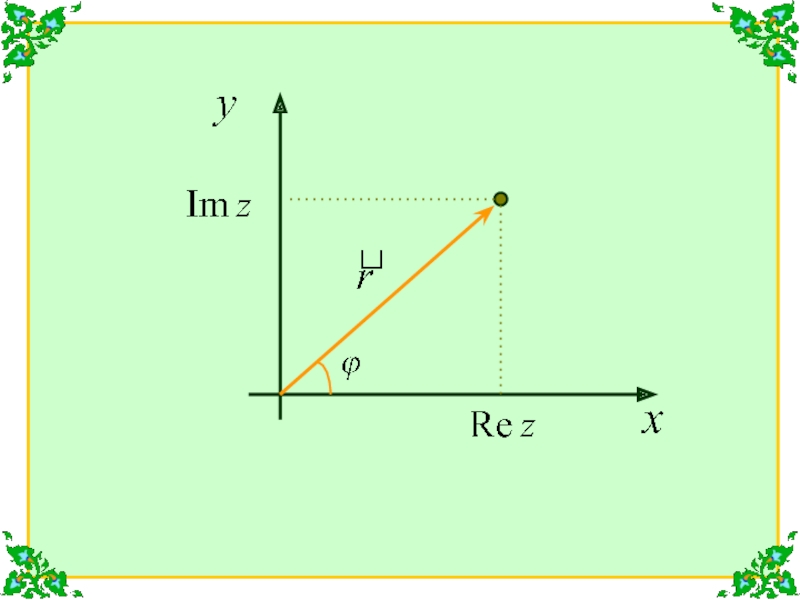
вектора называется модулем комплексного числа z и обозначается
Угол, образованный
радиус-вектором точки и осью х называется аргументом комплексного числа z и обозначается Из всех значений аргумента выделяется главное значение
удовлетворяющее условию