TheSlide.ru

22.8. ИНТЕГРИРОВАНИЕ ФКП Пусть на комплексной плоскости z дана кривая L

Содержание

1. 22.8. ИНТЕГРИРОВАНИЕ ФКП Пусть на комплексной плоскости z дана кривая L
2. L
3. Обозначимгде число Δzi изображается вектором, идущим из
4. Данная сумма будет интегральной. Предел этой суммы
5. Свойства интеграла ФКП1Интеграл от суммы (разности) двух
6. 2Постоянную величину можно выноситьза знак интеграла:
7. 3Если кривая L геометрически совпадает с кривой L1, но имеет противоположноенаправление, то:
8. 4Если кривая разбита на дуги L1 L2 …Ln то:
9. Вычисление интеграла ФКП сводится к вычислению криволинейного интеграла от функции действительного переменного.ПустьОбозначим
10. Тогда Поскольку
11. Переходим к пределу
12. Слайд 12
13. Эта формула показывает, что чтобы свести интеграл
14. и начальная и конечная точки кривой соответственно t0 и tnто исходный интеграл сводится к определенному:
15. ПРИМЕР.Вычислить интеграл:Где L – отрезок, соединяющий точки 0 и 1+i
16. L
17. Решение:Запишем уравнение отрезка в параметрическом виде:илиТогда
18. Слайд 18
19. Скачать презентанцию

Обозначимгде число Δzi изображается вектором, идущим из точки zi-1 в точку zi.-длина этого вектора, т.е. хорда, стягивающая соответствующую элементарную дугу.Внутри каждой элементарной дуги выбираем произвольную точку ξi.Составим сумму

Главная
Разное
22.8. ИНТЕГРИРОВАНИЕ ФКП Пусть на комплексной плоскости z дана кривая L

Слайды и текст этой презентации

Слайд 122.8. ИНТЕГРИРОВАНИЕ ФКП
Пусть на комплексной плоскости z дана кривая L.

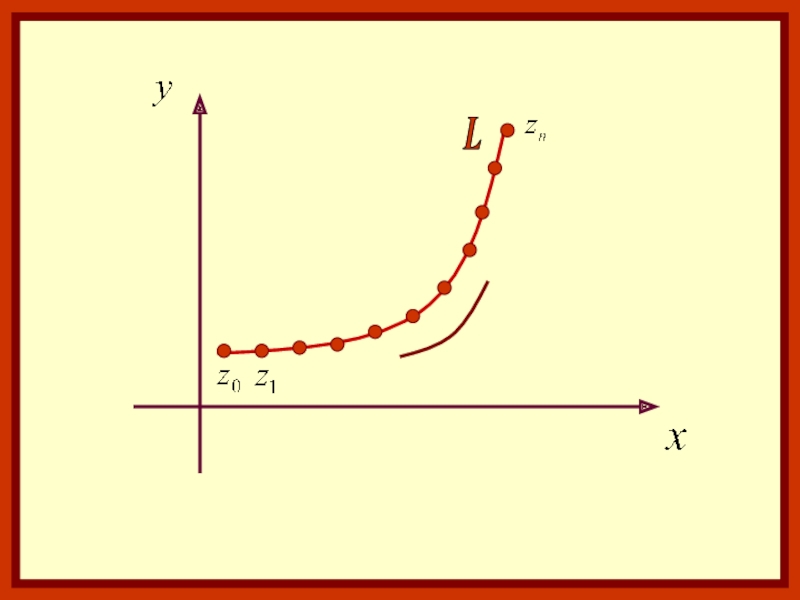
Граничные точки этой кривой: z0 и zn (если кривая замкнутая,

то z0=zn).
Установим положительное направление: от точки z0 к zn.
Предположим, что функция комплексного аргумента z непрерывна во всех точках этой кривой.
Разобьем кривую точками на элементарные дуги.

22.8. ИНТЕГРИРОВАНИЕ ФКППусть на комплексной плоскости z дана кривая L. Граничные точки этой кривой: z0 и zn

Слайд 2L

Слайд 3Обозначим
где число Δzi изображается вектором, идущим из точки zi-1 в

точку zi.
-длина этого вектора, т.е. хорда, стягивающая соответствующую элементарную дугу.
Внутри

каждой элементарной дуги выбираем произвольную точку ξi.
Составим сумму

Обозначимгде число Δzi изображается вектором, идущим из точки zi-1 в точку zi.-длина этого вектора, т.е. хорда, стягивающая

Слайд 4Данная сумма будет интегральной.
Предел этой суммы при стремлении к

нулю длин всех дуг будет интегралом функции f(z) по кривой

L:

Данная сумма будет интегральной. Предел этой суммы при стремлении к нулю длин всех дуг будет интегралом функции

Слайд 5Свойства интеграла ФКП
1
Интеграл от суммы (разности) двух или
нескольких функций

равен сумме (разности)
интегралов от этих функций:

Свойства интеграла ФКП1Интеграл от суммы (разности) двух или нескольких функций равен сумме (разности) интегралов от этих функций:

Слайд 62
Постоянную величину можно выносить
за знак интеграла:

2Постоянную величину можно выноситьза знак интеграла:

Слайд 73
Если кривая L геометрически совпадает с
кривой L1, но имеет

противоположное
направление, то:

3Если кривая L геометрически совпадает с кривой L1, но имеет противоположноенаправление, то:

Слайд 84
Если кривая разбита на дуги L1 L2 …Ln то:

4Если кривая разбита на дуги L1 L2 …Ln то:

Слайд 9Вычисление интеграла ФКП сводится к вычислению криволинейного интеграла от функции

действительного переменного.
Пусть
Обозначим

Вычисление интеграла ФКП сводится к вычислению криволинейного интеграла от функции действительного переменного.ПустьОбозначим

Слайд 10Тогда
Поскольку

Тогда Поскольку

Слайд 11Переходим к пределу

Переходим к пределу

Слайд 12

Слайд 13Эта формула показывает, что чтобы свести интеграл по комплексному аргументу

к вычислению обычного криволинейного интеграла, нужно выделить в подынтегральной функции

действительные и мнимые части

и умножить ее на

Если кривая L задана параметрически

Эта формула показывает, что чтобы свести интеграл по комплексному аргументу к вычислению обычного криволинейного интеграла, нужно выделить

Слайд 14и начальная и конечная точки кривой соответственно t0 и tn
то

исходный интеграл сводится к определенному:

и начальная и конечная точки кривой соответственно t0 и tnто исходный интеграл сводится к определенному:

Слайд 15ПРИМЕР.
Вычислить интеграл:
Где L – отрезок, соединяющий
точки 0 и 1+i

ПРИМЕР.Вычислить интеграл:Где L – отрезок, соединяющий точки 0 и 1+i

Слайд 16L

Слайд 17Решение:
Запишем уравнение отрезка в параметрическом виде:
или
Тогда

Решение:Запишем уравнение отрезка в параметрическом виде:илиТогда

Слайд 18

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей