3. 2 Понятия о результате, точности и погрешности измерения. Уравнение

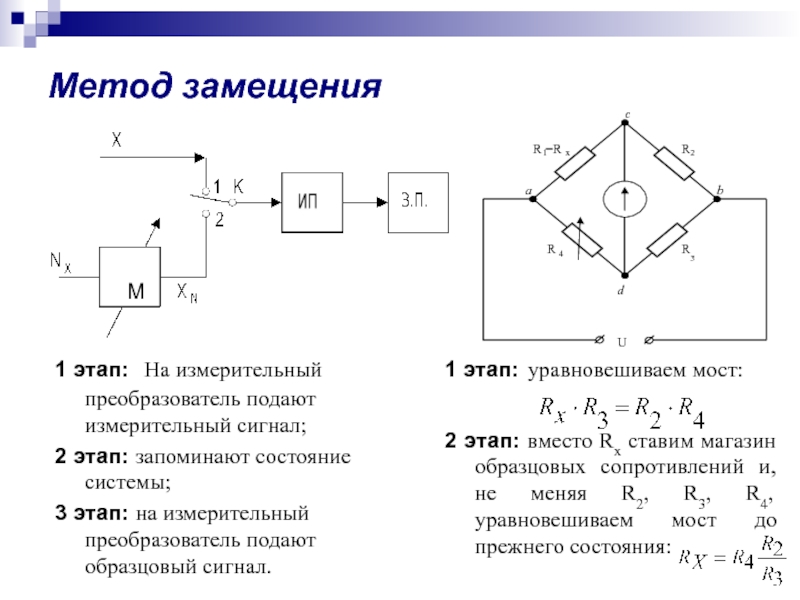
Уравнение измерений.
Результатом измерения (РИ) будем называть значение величины,

найденное путем ее измерения.

Характерные особенности РИ:
определяется экспериментальным путем;
представляет собой число, которое при абсолютных измерениях является именованным с указанием единицы измеряемой величины;
содержит показатели точности, без которых нельзя судить об качестве измерения и использовать данный результат измерения совместно с результатами других измерений.
содержит (во многих случаях) и результат идентификации входного сигнала и его модели, т. е. указание характерных признаков принятой модели

величины.

Точность является основным качеством измерения и отражает близость РИ к

истинному значению измеряемой величины.

Уравнение измерения связывает между собой:
истинное значение измеряемой величины X,
результат измерения ,
погрешность ,
числовое значение входного кода меры Nx,
цену ступени квантования выходной величины меры
коэффициент масштабного преобразователя К.

в него уравнений меры (М) и масштабного преобразователя (МП).

ряда с одинаковым интервалом между размерами ,

размер которого принимаем равным единице данной величины или ее доле:

Эта операция реализуется последовательно во времени

Операцию сравнения для выявления знака разности размеров величины X и xN.
Y = sign( X - xN )

В результате конечного шага отработки

Числовое значение ФВ:

числом, по значению обратно пропорциональным измеряемой величине X, и не

может служить ее числовым значением!
Такой набор ЭСИ для проведения измерения не используется!

Nном равномерными ступенями,
Nном каналами;
Nном УС.

время измерения: tизм = tус

одноэтапный алгоритм

числовое

значение результата измерения
определяется по номеру старшего из сработавших УС.

детерминированный алгоритм Уравнение метода:
первого метода сопоставления:

время измерения: tизм = tус

алгоритм измерения:
При измерении нулевые метки мер

сдвигаются на измеряемую величину X;
затем определяют номер N1 «совпавшей» метки.
Тогда из уравнения определяют
Уравнение метода: (например, для n=10)

измерения:



алгоритм измерения:
Мера управляется оператором либо автоматически по знаку разности

( X–xN ) на
выходе УС. Характерной особенностью этого метода является изменение
выходной величины меры – xN вплоть до уравнивания со значением X.

Погрешность измерения X определяется только погрешностью воспроизведения меры.

Уравнение метода:

задан и повторяется при каждом измерении, стохастические, при которых величина изменяется

случайно, но имеет заданное распределение.

алгоритм «исчерпывания»







Результат измерения

алгоритм поразрядного уравновешивания


Результат измерения в двоичном коде:

В этом случае ОРМ управляется от генератора случайных чисел с

равномерным законом распределения от 0 до .
Максимальное значение случайного процесса Xmax(t) должно быть меньше номинального значения выходной величины меры .




Результат измерения:

магазин образцовых сопротивлений и, не меняя R2, R3, R4, уравновешиваем

мост до прежнего состояния:

М

1 этап: На измерительный преобразователь подают измерительный сигнал;
2 этап: запоминают состояние системы;
3 этап: на измерительный преобразователь подают образцовый сигнал.