Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
337792
Содержание
- 1. 337792
- 2. Формы мышленияЛогические выраженияЛогические операцииЗаконы
- 3. Формы мышления и история развития алгебры
- 4. Формы мышления и история развития алгебры
- 5. Логика – это наука о формах и
- 6. Примеры высказыванийИстинное высказывание: «Буква «А» - гласная».Ложное
- 7. Примеры умозаключенийДано высказывание: «Все углы равнобедренного треугольника
- 8. Логические выражения Логическая переменная – простое высказывание,
- 9. Логические операции Каждое составное высказывание можно выразить
- 10. Инверсия - логическое отрицаниеОт лат. inversio -
- 11. Конъюнкция - логическое умножениеОт лат. conjunctio -
- 12. Дизъюнкция - логическое сложениеОт лат. disjunctio –
- 13. Импликация - логическое следованиеРезультат логического следования является
- 14. Эквивалентность - логическое равенствоРезультат логического равенства является
- 15. «Точка Х принадлежит интервалу [A;B]»Упражнения по записи
- 16. В С
- 17. Упражнения c логическими выражениямиПо мишеням произведено три
- 18. Законы алгебры логикиA
- 19. Решение содержательных задач с помощью алгебры логикиАлгоритмВнимательно
- 20. Решение логических задач с помощью алгебры логики«Синоптик
- 21. Решение содержательных задач табличным способомВ оркестр приняли
- 22. Решение содержательных задач с помощью рассужденийВадим, Сергей
- 23. Таблицы истинности1Докажите эквивалентность булевских выражений А
- 24. Логические основы компьютера. Базовые логические элементыЛогический
- 25. КонъюнкторЛогические основы компьютера. Базовые логические элементыДизъюнкторИнверторАВF=А*ВАВF=А+ВАА
- 26. Логические основы компьютера. Построение логических схемВычертить
- 27. Логические основы компьютера. Построение логических схемПо
- 28. Логические основы компьютера. Одноразрядный двоичный полусумматорСумматор
- 29. Логические основы компьютера. Одноразрядный двоичный сумматорПри
- 30. Логические основы компьютера. ТриггерТриггер (trigger – защелка,
- 31. Логические основы компьютера. РегистрыТриггер был создан советским
- 32. Контрольная работа по теме «Основы алгебры логики и логические основы компьютера»
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Формы мышления
Логические
выражения
Логические
операции
Законы
алгебры логики
Таблицы
истинности
Логические задачи
Основы алгебры логики
Логические
основы компьютера
Слайд 3Формы мышления и история развития
алгебры логики
История логики насчитывает около
двух с половиной тысячелетий. Первые учения о формах и способах
мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является Аристотель (384-322 гг. до н.э.) – древнегреческий философ, который впервые отделил логические формы мышления от его содержания.Алгебра логики – наука об операциях, аналогичных математическим, над высказываниями или над объектами, которые могут принимать только два значения – «ИСТИНА» или «ЛОЖЬ».
В 1842 году английский математик Джорж Буль разработал математическую логику или алгебру логики, которую впоследствии стали называть «булевой алгеброй».
Спустя 100 лет алгебра логики стала основой теории цифровых вычислительных машин, ее используют в компьютерной логике, электронике, в основе всех микропроцессорных операций.
Слайд 4Формы мышления и история развития
алгебры логики
Многие философы и математики
развивали отдельные положения логики и иногда даже намечали контуры современного
исчисления высказываний, но ближе всех к созданию математической логики подошел уже во второй половине XVII века выдающийся немецкий ученый Готфрид Вильгельм Лейбниц (1646— 1716), указавший пути для перевода логики “из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются совершенно точно”. Лейбниц надеялся даже, что в будущем философы, вместо того чтобы бесплодно спорить, станут брать бумагу и вычислять, кто из них прав. При этом в своих работах Лейбниц затрагивал и двоичную систему счисления.Уже в XIX веке стало понятно, что система Буля хорошо подходит для описания электрических переключательных схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому, как утверждение может быть либо истинным, либо ложным. А еще несколько десятилетий спустя, уже в XX столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.
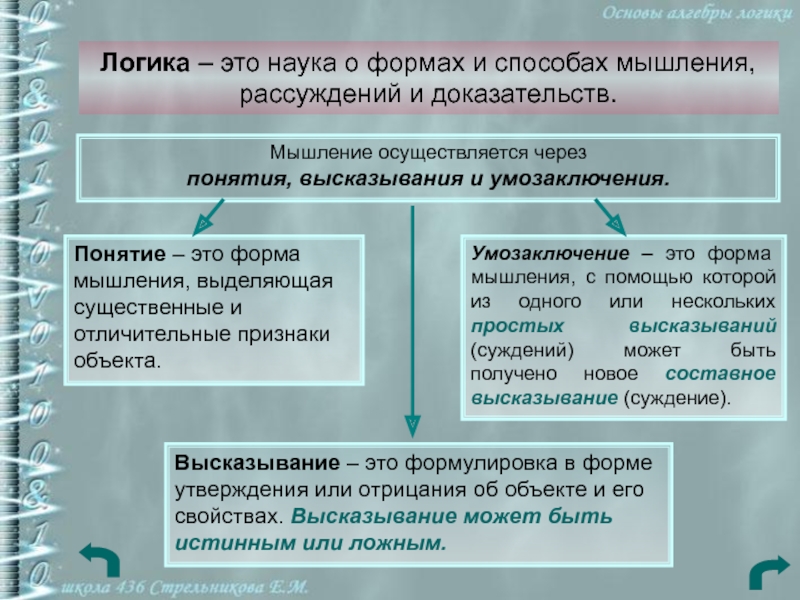
Слайд 5Логика – это наука о формах и способах мышления, рассуждений
и доказательств.
Мышление осуществляется через
понятия, высказывания и умозаключения.
Понятие – это
форма мышления, выделяющая существенные и отличительные признаки объекта.Высказывание – это формулировка в форме утверждения или отрицания об объекте и его свойствах. Высказывание может быть истинным или ложным.
Умозаключение – это форма мышления, с помощью которой из одного или нескольких простых высказываний (суждений) может быть получено новое составное высказывание (суждение).
Слайд 6Примеры высказываний
Истинное высказывание: «Буква «А» - гласная».
Ложное высказывание: «Компьютер был
изобретен в середине XIX века».
Какие из предложений являются высказываниями? Какие
из высказываний истинные?1. Какой длины эта лента?
2. Прослушайте сообщение.
3. Делайте утреннюю зарядку!
4. Назовите устройства ввода информации.
5. Кто отсутствует?
6. Париж – столица Англии.
7. Число 11 является простым.
8. 4+5=10
9. Без труда не вытащишь и рыбку из пруда.
10. Сложите числа 2 и 5.
11. Некоторые медведи живут на Севере.
12. Все медведи – бурые.
13. Чему равно расстояние от Москвы до Ленинграда?
14. Сумма углов треугольника – 180 градусов.
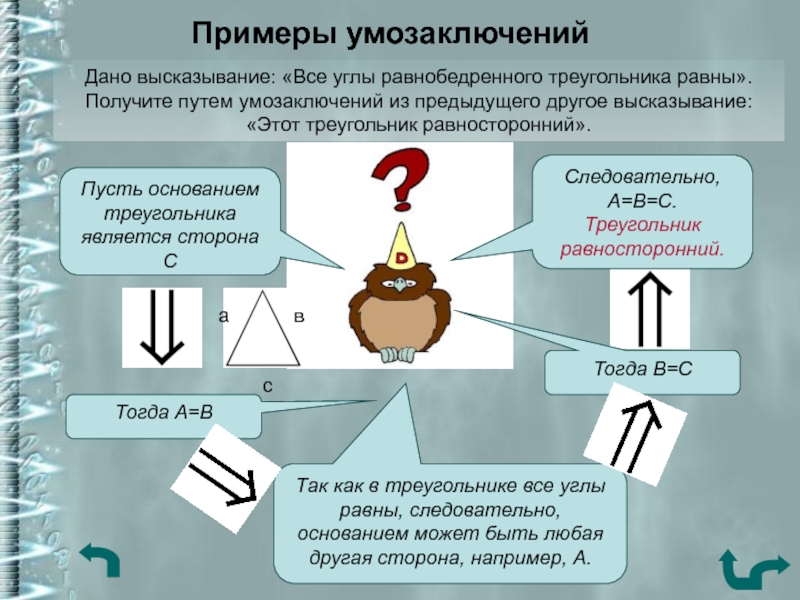
Слайд 7Примеры умозаключений
Дано высказывание: «Все углы равнобедренного треугольника равны». Получите путем
умозаключений из предыдущего другое высказывание: «Этот треугольник равносторонний».
Тогда А=В
Так как
в треугольнике все углы равны, следовательно, основанием может быть любая другая сторона, например, А.Тогда В=С
Следовательно, А=В=С. Треугольник равносторонний.
Пусть основанием треугольника является сторона С
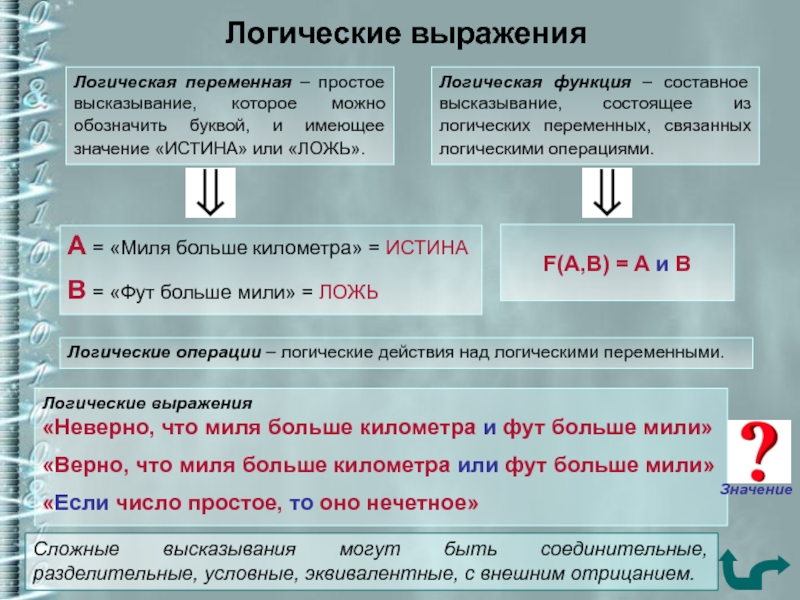
Слайд 8Логические выражения
Логическая переменная – простое высказывание, которое можно обозначить
буквой, и имеющее значение «ИСТИНА» или «ЛОЖЬ».
Логическая функция –
составное высказывание, состоящее из логических переменных, связанных логическими операциями. Логические операции – логические действия над логическими переменными.
А = «Миля больше километра» = ИСТИНА
В = «Фут больше мили» = ЛОЖЬ
F(A,B) = A и В
Логические выражения
«Неверно, что миля больше километра и фут больше мили»
«Верно, что миля больше километра или фут больше мили»
«Если число простое, то оно нечетное»
Сложные высказывания могут быть соединительные, разделительные, условные, эквивалентные, с внешним отрицанием.
Значение
Слайд 9Логические операции
Каждое составное высказывание можно выразить в виде формулы
(логического выражения), в которую войдут логические переменные, обозначающие высказывания, и
знаки логических операций, обозначающие логические функции.ИСТИНА – 1
ЛОЖЬ - 0
Таблица истинности определяет значение сложного высказывания при всех возможных значениях простых высказываний
Слайд 10Инверсия - логическое отрицание
От лат. inversio - переворачиваю
Логическое отрицание делает
истинное высказывание ложным и, наоборот, ложное – истинным.
Таблица истинности функции
логического отрицанияПример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Луна – спутник Земли» = ИСТИНА
Не А – «Неверно, что число 10 – четное» = ЛОЖЬ
Не В – «Неверно, что число 10 – отрицательное» = ИСТИНА
Не С – «Неверно, что Луна – спутник Земли» = ЛОЖЬ
В переводе на естественный язык
«Не А»
«Неверно, что А»
ИСТИНА – 1
ЛОЖЬ - 0
Слайд 11Конъюнкция - логическое умножение
От лат. conjunctio - связываю
Результат логического умножения
является истинным тогда и только тогда, когда истинны все входящие
в него простые высказывания.Таблица истинности функции логического умножения
В переводе на естественный язык
«и А, и В» «как А, так и В»
«А вместе с В» «А несмотря на В»
«А, в то время как В»
И , , and, &, *, ·
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 кратно 2» = ИСТИНА
А и В – «Число 10 – четное и отрицательное» - ЛОЖЬ
А и С – «Число 10 как четное, так и кратно 2» - ИСТИНА
Слайд 12Дизъюнкция - логическое сложение
От лат. disjunctio – различаю
Результат логического сложения
является истинным тогда, когда истинно хотя бы одно из входящих
в него простых высказываний.В переводе на естественный язык
«А или В»
Таблица истинности функции логического сложения
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ
А или В – «Число 10 – четное или отрицательное» - ИСТИНА
А или С – «Число 10 четное или простое» - ИСТИНА
В или С – «Число 10 отрицательное или простое» - ЛОЖЬ
ИЛИ, , or, +
Слайд 13Импликация - логическое следование
Результат логического следования является ложным тогда и
только тогда, когда из истины следует ложь.
От лат. implicatio –
тесно связыватьТаблица истинности функции логического следования
А – условие, В - следствие
В переводе на естественный язык
«если А, то В» «В, если А»
«Когда А, тогда В»
«А достаточно для В»
«А только тогда, когда В»
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ
А В – «Если число 10 – четное,
то оно - отрицательное» - ЛОЖЬ
А С – «Число 10 простое, если четное» - ЛОЖЬ
«Если число делится на 10, то оно делится на 5» ИСТИНА
Слайд 14Эквивалентность - логическое равенство
Результат логического равенства является истинным тогда и
только тогда, когда оба высказывания одновременно либо истинны, либо ложны.
От
лат. aeguivalens – равноценноеТаблица истинности функции логического равенства
В переводе на естественный язык
«А эквивалентно В»
«А только тогда и только тогда, когда В»
=,
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ
А В – «Число 10 – четное, тогда и только тогда, когда оно - отрицательное» - ЛОЖЬ
В С – «Число 10 такое же простое, как и отрицательное» ИСТИНА
Слайд 15«Точка Х принадлежит интервалу [A;B]»
Упражнения по записи высказываний в виде
логических выражений
«Летом Петя поедет в деревню и, если будет хорошая
погода, то он будет рыбачить.»1
А
В
С
При составлении логического выражения необходимо учитывать порядок выполнения логических операций:
1. действия в скобках
2. инверсия
3. конъюнкция
4. дизъюнкция
5. импликация
6. эквивалентность
F=A * (B C)
2
(X>=A) * (X<=B)
«Точка Х не принадлежит интервалу [A;B]»
3
(X>=A) * (X<=B)
(X «Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя.» 4 В С D – идет дождь В (С D)
Слайд 16
В С
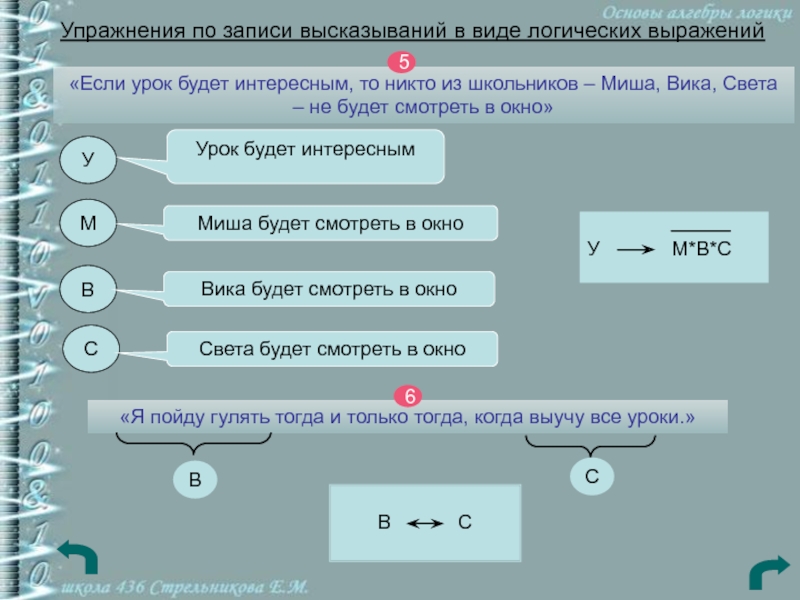
Упражнения по записи высказываний в виде логических выражений
«Если урок будет
интересным, то никто из школьников – Миша, Вика, Света – не будет смотреть в окно»5
У
М
В
С
Урок будет интересным
Миша будет смотреть в окно
Вика будет смотреть в окно
Света будет смотреть в окно
У М*В*С
«Я пойду гулять тогда и только тогда, когда выучу все уроки.»
6
В
С
Слайд 17Упражнения c логическими выражениями
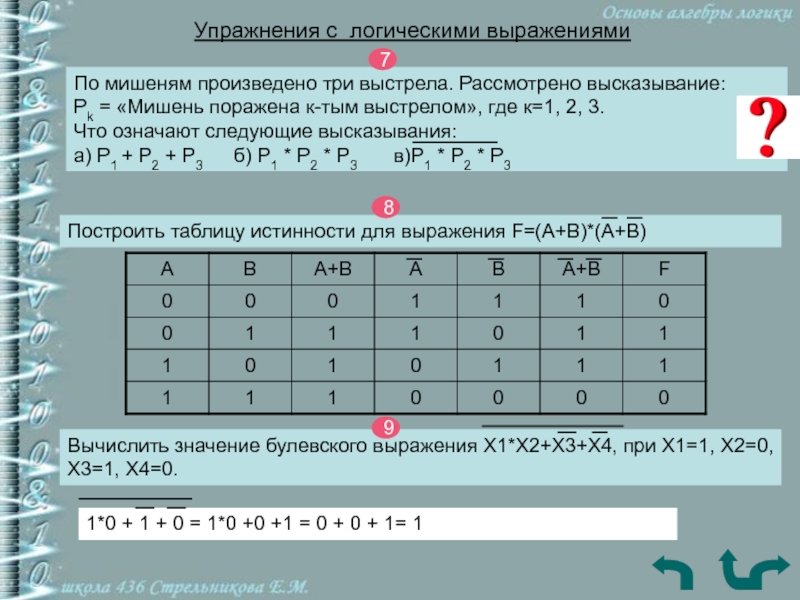
По мишеням произведено три выстрела. Рассмотрено высказывание:
Pk = «Мишень поражена к-тым выстрелом», где к=1, 2, 3.
Что означают следующие высказывания: а) P1 + P2 + P3 б) P1 * P2 * P3 в)P1 * P2 * P37
Построить таблицу истинности для выражения F=(A+B)*(A+B)
8
Вычислить значение булевского выражения X1*X2+X3+X4, при X1=1, X2=0, X3=1, X4=0.
9
1*0 + 1 + 0 = 1*0 +0 +1 = 0 + 0 + 1= 1
Слайд 19Решение содержательных задач с помощью алгебры логики
Алгоритм
Внимательно изучить условие
Выделить простые
высказывания и обозначить их буквами
Записать условие задачи на языке алгебры
логикиСоставить формулу, в которой объединить логическим умножением формулы каждого утверждения, приравнять произведение к 1
Упростить формулу согласно законам – минимизировать логическое выражение
Проанализировать результат или построить таблицу истинности результирующего выражения и найти по таблице значения переменных, для которых значение функции равно 1
Слайд 20Решение логических задач с помощью алгебры логики
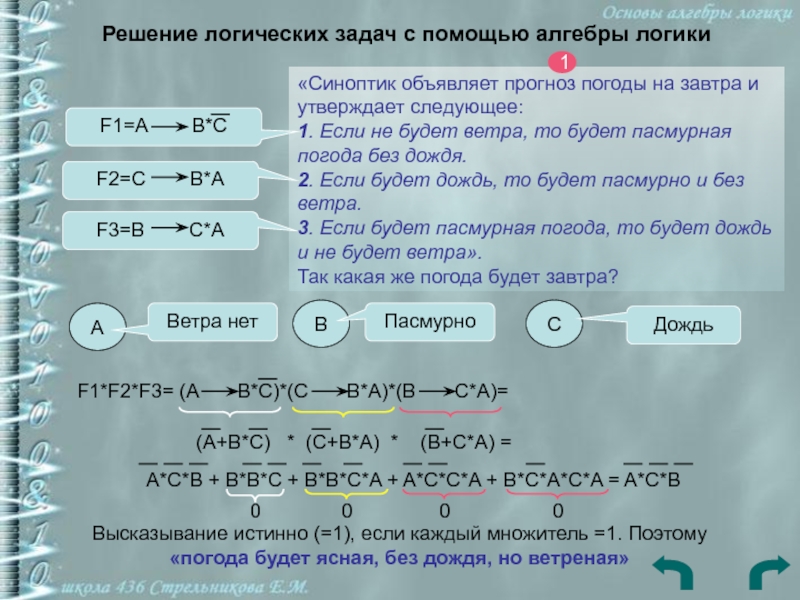
«Синоптик объявляет прогноз погоды
на завтра и утверждает следующее: 1. Если не будет ветра, то
будет пасмурная погода без дождя. 2. Если будет дождь, то будет пасмурно и без ветра. 3. Если будет пасмурная погода, то будет дождь и не будет ветра». Так какая же погода будет завтра?1
А
В
С
Ветра нет
Пасмурно
Дождь
F1=A B*C
F2=C B*A
F3=B C*A
F1*F2*F3= (A B*C)*(C B*A)*(B C*A)=
(A+B*C) * (C+B*A) * (B+C*A) =
A*C*B + B*B*C + B*B*C*A + A*C*C*A + B*C*A*C*A = A*C*B
0
0
0
0
Высказывание истинно (=1), если каждый множитель =1. Поэтому
«погода будет ясная, без дождя, но ветреная»
Слайд 21Решение содержательных задач табличным способом
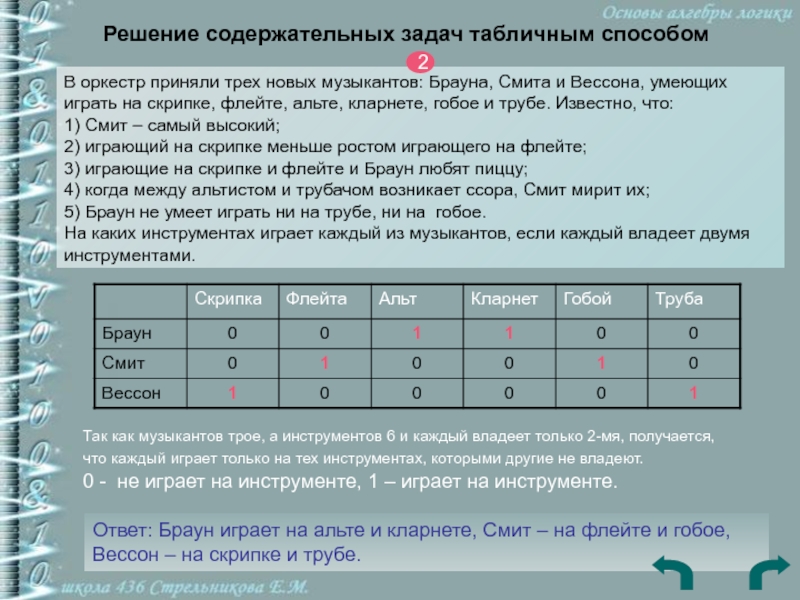
В оркестр приняли трех новых музыкантов:
Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте,
кларнете, гобое и трубе. Известно, что: 1) Смит – самый высокий; 2) играющий на скрипке меньше ростом играющего на флейте; 3) играющие на скрипке и флейте и Браун любят пиццу; 4) когда между альтистом и трубачом возникает ссора, Смит мирит их; 5) Браун не умеет играть ни на трубе, ни на гобое. На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами.Так как музыкантов трое, а инструментов 6 и каждый владеет только 2-мя, получается, что каждый играет только на тех инструментах, которыми другие не владеют.
0 - не играет на инструменте, 1 – играет на инструменте.
Ответ: Браун играет на альте и кларнете, Смит – на флейте и гобое, Вессон – на скрипке и трубе.
2
Слайд 22Решение содержательных задач с помощью рассуждений
Вадим, Сергей и Михаил изучают
различные иностранные языки: китайский, японский и арабский. На вопрос, какой
язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый?Решение.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе – ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил – японский, Вадим – арабский.
3
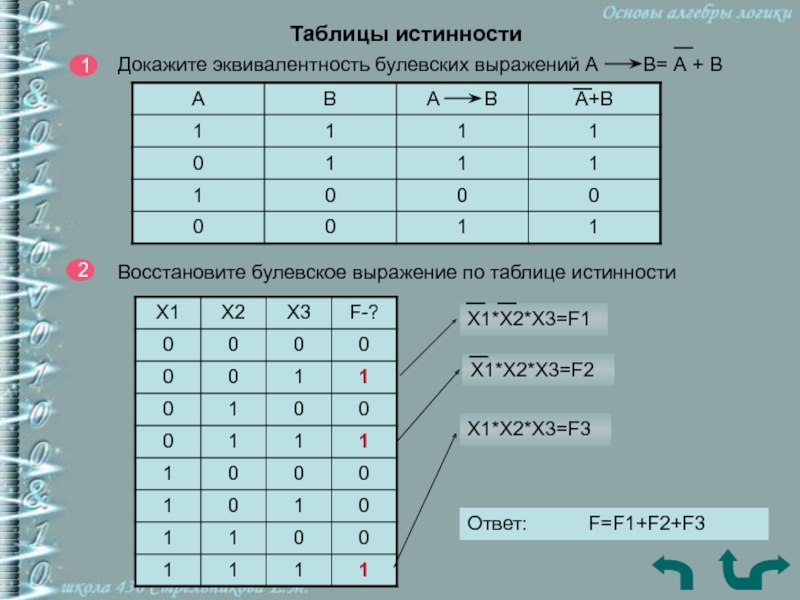
Слайд 23Таблицы истинности
1
Докажите эквивалентность булевских выражений А В=
А + В
2
Восстановите булевское выражение по таблице истинности
Х1*Х2*Х3=F1
Х1*Х2*Х3=F2
Х1*Х2*Х3=F3
Ответ:
F=F1+F2+F3Слайд 24Логические основы компьютера.
Базовые логические элементы
Логический элемент компьютера (вентиль) -
это электронная схема, реализующая базовую логическую операцию и характеризующаяся наличием
сигнала на входе и выходе элемента.С помощью базовых логических элементов можно реализовать любую логическую функцию, выполняющую арифметические операции или хранение информации.
Обычно у вентилей от двух до восьми входов и один или два выхода.
Состояние логических элементов характеризуется таблицей входов-выходов логических элементов. На входы логических элементов подаются электрические сигналы высокого уровня напряжения (+5 вольт) – «логическая 1», и низкого уровня напряжения (около 0 вольт) – «логический 0»
И (конъюнктор), ИЛИ (дизъюнктор), НЕ (инвертор)
Чтобы построить логическую схему необходимо:
1) определить число логических переменных
2) определить количество базовых логических операций и их порядок
3) выбрать вентиль для каждой операции и соединить их в порядке выполнения логических операций.
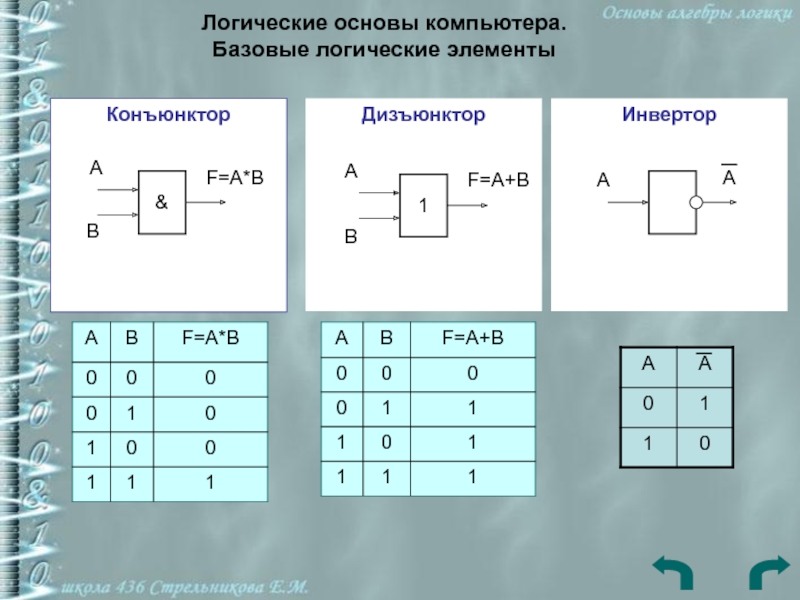
Слайд 25Конъюнктор
Логические основы компьютера.
Базовые логические элементы
Дизъюнктор
Инвертор
А
В
F=А*В
А
В
F=А+В
А
А
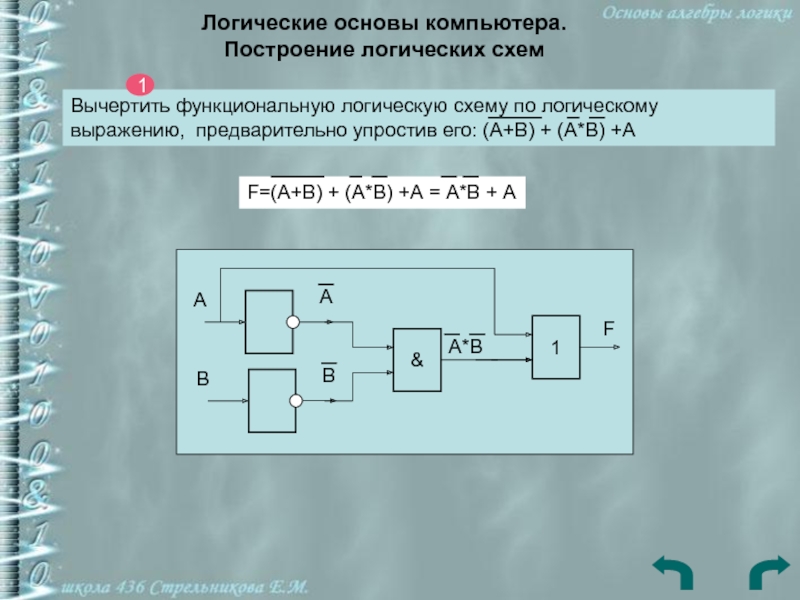
Слайд 26Логические основы компьютера.
Построение логических схем
Вычертить функциональную логическую схему по
логическому выражению, предварительно упростив его: (А+В) + (А*В) +А
1
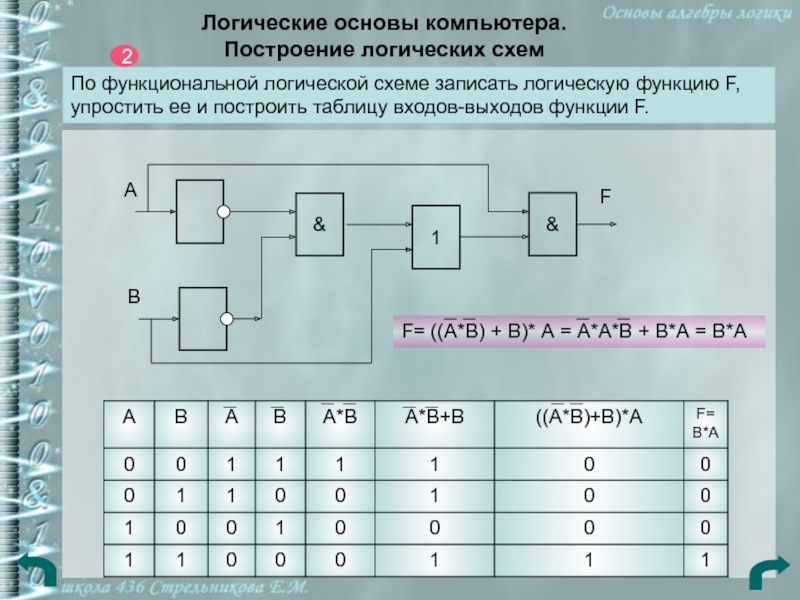
Слайд 27Логические основы компьютера.
Построение логических схем
По функциональной логической схеме записать
логическую функцию F, упростить ее и построить таблицу входов-выходов функции
F.А
В
&
1
&
F
F= ((А*В) + В)* А = А*А*В + В*А = В*А
2
Слайд 28Логические основы компьютера.
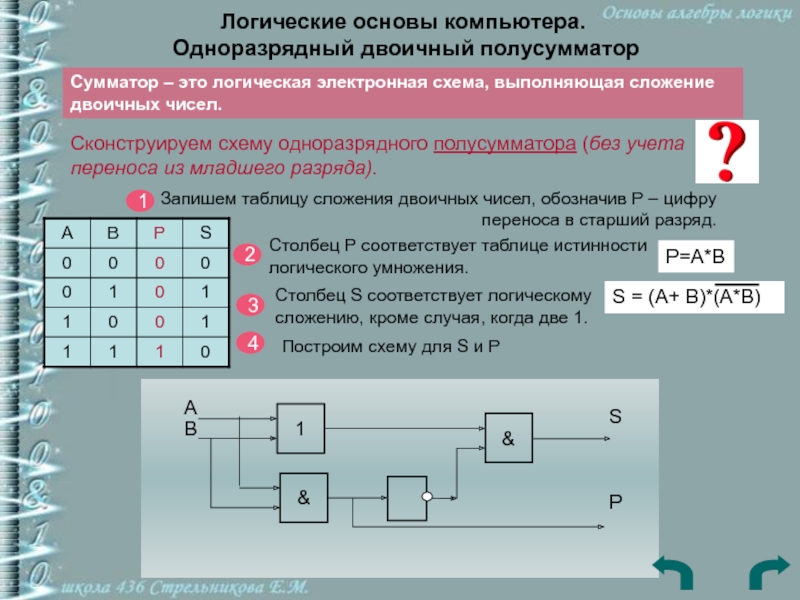
Одноразрядный двоичный полусумматор
Сумматор – это логическая электронная
схема, выполняющая сложение двоичных чисел.
Сконструируем схему одноразрядного полусумматора (без учета
переноса из младшего разряда).Запишем таблицу сложения двоичных чисел, обозначив Р – цифру переноса в старший разряд.
1
2
Столбец Р соответствует таблице истинности логического умножения.
3
Столбец S соответствует логическому сложению, кроме случая, когда две 1.
4
Построим схему для S и P
Р=А*В
Слайд 29Логические основы компьютера.
Одноразрядный двоичный сумматор
При сложении чисел А и
В в каждом разряде на вход сумматора должны подаваться три
двоичных сигнала: цифра А - первое слагаемое, цифра В - второе слагаемое, P0 – перенос из предыдущего разряда. Выходы одноразрядного сумматора: S – сумма, Р – перенос цифры из текущего разряда в старший.Таблица входов-выходов
Вид одноразрядного сумматора в виде единого функционального узла (условное обозначение)
В
А
Р0
Р
S
S = (A*B) + (А*Р0 ) + (B*Р0)
Вид трехразрядного сумматора
Слайд 30Логические основы компьютера. Триггер
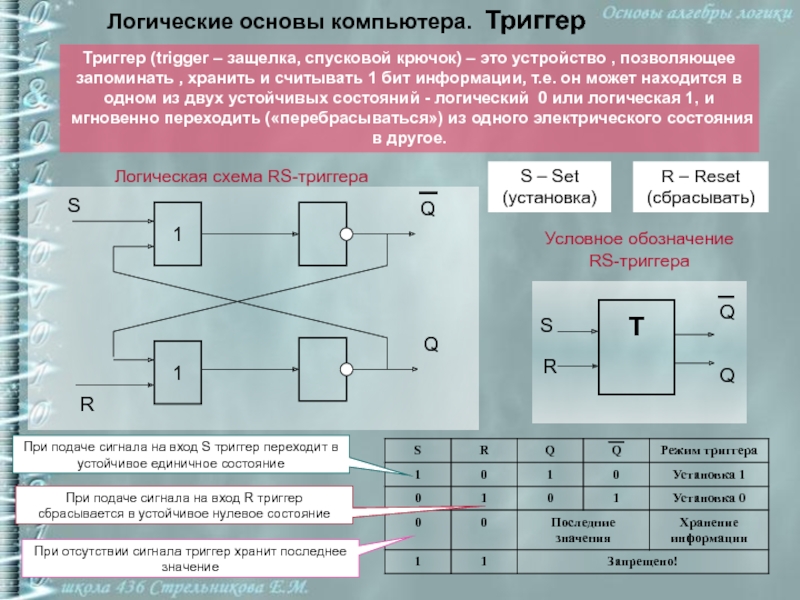
Триггер (trigger – защелка, спусковой крючок) –
это устройство , позволяющее запоминать , хранить и считывать 1
бит информации, т.е. он может находится в одном из двух устойчивых состояний - логический 0 или логическая 1, и мгновенно переходить («перебрасываться») из одного электрического состояния в другое.Логическая схема RS-триггера
Условное обозначение
RS-триггера
1
1
S
R
Q
Q
S – Set (установка)
R – Reset (сбрасывать)
При подаче сигнала на вход S триггер переходит в устойчивое единичное состояние
При подаче сигнала на вход R триггер сбрасывается в устойчивое нулевое состояние
При отсутствии сигнала триггер хранит последнее значение
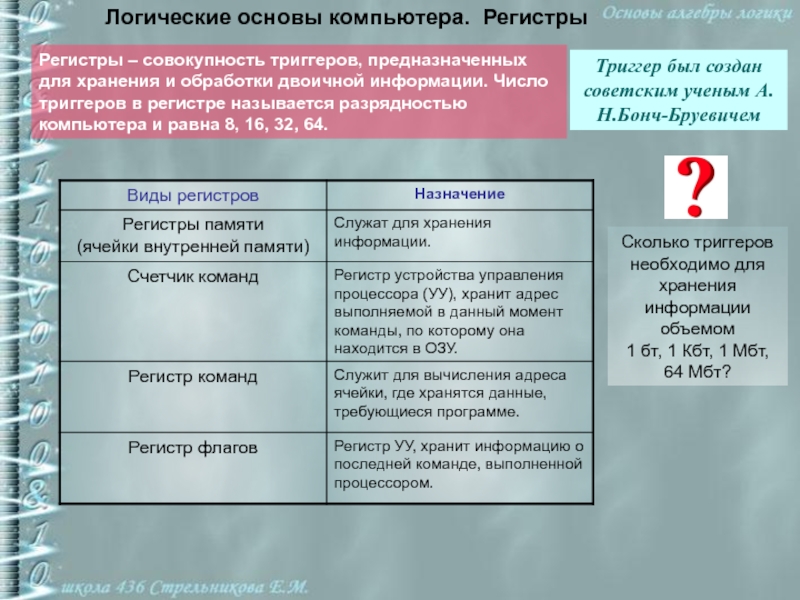
Слайд 31Логические основы компьютера. Регистры
Триггер был создан советским ученым А.Н.Бонч-Бруевичем
Сколько триггеров
необходимо для хранения информации объемом 1 бт, 1 Кбт, 1
Мбт, 64 Мбт?Регистры – совокупность триггеров, предназначенных для хранения и обработки двоичной информации. Число триггеров в регистре называется разрядностью компьютера и равна 8, 16, 32, 64.










![337792 «Точка Х принадлежит интервалу [A;B]»Упражнения по записи высказываний в виде логических «Точка Х принадлежит интервалу [A;B]»Упражнения по записи высказываний в виде логических выражений«Летом Петя поедет в деревню и,](/img/thumbs/16e24a7f54c5bbf6c1f03bc35bffb858-800x.jpg)