Слайд 16.3. Корпускулярно-волновой дуализм. Принцип неопределенности Гейзенберга
Итак, было установлено, что микроскопические
объекты (электроны, фотоны, атомы и др.) обладают как корпускулярными (дискретность,
неделимость), так и волновыми (способность к дифракции) свойствами.
Для согласования этих свойств в рамках единого представления используется концепция корпускулярно-волнового дуализма. Она применима ко всем микрообъектам.
Согласно этой концепции, микрочастицы (электрон, фотон и т.д.) являются материальными объектами, обладающими внутренне непротиворечивыми свойствами. Вся совокупность этих свойств не находит соответствия ни в одном из интуитивно понятных нам представлений. При этом некоторая часть этих свойств имеет сходство со свойствами классических частиц (взятых как представление, идеальный объект, интуитивно понятный элемент теоретического рассмотрения). Другие свойства подобны свойствам классических волновых процессов.
Имеющиеся отличия свойств микрообъектов от свойств привычных макроскопических аналогов не является непреодолимым препятствием для построения их верного теоретического описания.
Слайд 2Помимо отмеченного подобия некоторых установленных свойств микрообъектов свойствам классических волн
и корпускул, есть и важные отличия.
В частности, способность микрообъектов к
дифракции, как отмечалось ранее, определяется недетерминированным характером их поведения, наилучшим образом математически описываемым через неочевидное понятие «волны вероятности» – а не связью с распространением волн в какой-либо материальной среде.
Корпускулярные свойства микрообъектов также имеют свои особенности в сравнении с классическим аналогами.
Частица в классической физике представляется (на интуитивном уровне) в виде жесткого шарика, в пределе – «материальной точки».
Концепция материальной точки предполагает, что текущее состояние частицы
исчерпывающе описывается значениями координат (x, y, z) и проекций импульса (px, py, pz). Эти значения принципиально могут быть определены
(вычислены или измерены) со сколь угодно высокой точностью.
В отношении микрообъектов эта концепция оказывается неверной или ограниченно применимой. (Состояние квантовой частицы не описывается этим набором параметров.)
Слайд 3Корпускулярные свойства микрочастиц, определенные в результате экспериментов, состоят в следующем:
из их совокупности (электронного газа, излучения в полости и т.д.)
можно выделить лишь дискретные порции массы, заряда, энергии, импульса и т.д. Такая порция и представляет собой частицу (электрон, фотон, …).
При этом ниоткуда не следует, что такая частица сосредоточена в маленьком неизменном шарике (материальной точке) и что ее состояние исчерпывающе
характеризуется набором координат (x, y, z) и проекций импульса (px, py, pz).
Более того, результаты экспериментов по дифракции на кристаллах показывают, что микрочастицы бывают в значительной степени делокализованы – поскольку могут «одновременно» взаимодействовать со многими атомами вещества.
При этом к элементарным (неделимым) частицам неприменимо понятие их собственного размера как расстояния между отдельными их частями – поскольку такие части отсутствуют.
Корректное (подтвержденное практикой) описание свойств микрообъектов, не использующее представление об их локальности, дается нерелятивистской квантовой механикой (для массивных частиц) и квантовой электродинамикой (для фотонов).

Слайд 4Вместе с тем, общепринятым является принцип соответствия, требующий, чтобы новая
общая теория включала в себя более старые подтвержденные классические теории
в качестве предельного случая, (почти) реализующегося для определенного диапазона условий.
Приблизительное положение границы, за которой могут использоваться классические представления о локализованных частицах, имеющих определенные значения координат и импульсов, дается так называемыми
Werner Karl Heisenberg (1901-1976)
«соотношениями неопределенностей».
Они представляют собой математическое выражение «принципа неопределенности», сформулированного в 1927 г. В. Гейзенбергом и ограничивающего возможность использования классически определенных величин к микрообъектам.
Первое из соотношений неопределенностей математически выражается формулой:
xpx 2ħ
~
Слайд 5 xpx 2ħ
Здесь x и px – величины неопределенности координаты
частицы и проекции ее импульса на ту же ось.
Подобные соотношения
независимо друг от друга должны действовать и для двух других осей:
ypy 2ħ и zpz 2ħ
Неравенства должны выполняться «по порядку величины», поэтому множитель 2 иногда опускают.
Постулируется связь между величинами неопределенности определения (это слово может иметь разные значения) сопряженных характеристик микрообъекта.
Микрочастица не может одновременно иметь точных значений координат и импульса. Поэтому ее движение не может быть охарактеризовано точной траекторией – так же, как траекторией не может характеризоваться распространение волн.
К примеру, если координата частицы точно задана, соответствующая проекция импульса полностью неопределена (может принимать произвольные значения). И наоборот – определение точного значения проекции импульса частицы приводит к утрате информации о соответствующей координате.
~
~
~
Слайд 6По Гейзенбергу, принцип неопределенности выражает фундаментальный закон природы, доказываемый совокупностью
наблюдений.
Трактовки принципа неопределенности могут различаться в зависимости от используемой модели
описания микрообъектов.
В рамках квантовой механики принцип неопределенности выводится как следствие ее постулатов. Доказываемому утверждение, согласно которому для тех состояний электрона, для которых точно определена его координата, не определено (математически не имеет конкретного значения) величина соответствующей проекции его импульса, и наоборот.
Еще один подход к трактовке соотношения неопределенностей состоит в прямом учете волновых эффектов, связанных с представлением частицы в качестве пакета волн вероятности.
Неопределенность координаты отождествляют с пространственным размером пакета x (по ширине главного максимума). Неопределенность импульса связывают с шириной используемого при построении пакета интервала значений волнового вектора k.
Слайд 7Уже отмечалось, что параметры
волнового пакета связаны как:
xk=2
Положив px= ħk , получаем
выражение, формально совпадающее с соотношением
неопределенностей (но в виде равенства):
xpx = 2ħ
Один из предельных случаев – гармоническая волна де Бройля, для которой волновой вектор (импульс) точно определен, а плотность вероятности
обнаружения частицы распределена равномерно (равна A2 при всех x).
Другой предельный случай – «точечный» пакет волн с неограниченным частотным спектром (интервалом волновых чисел).
Слайд 8Таким образом, в данной интерпретации соотношение неопределенностей представляется следствием свойств
преобразования Фурье, описывающего связь функций с их пространственными частотами (волновыми
числами).
Для корпускул «в классическом понимании» соотношение неопределенностей может выражать принципиальную невозможность точного измерения (при использовании сколь угодно совершенной техники) пары входящих в нее величин для одного микрообъекта. Предполагается, что сам факт измерения одной из таких величин вносит непредсказуемую погрешность в результат измерения второй величины.
При этом невозможность измерения точных значений отождествляется с их несуществованием.
Для обоснования соотношений неопределенности без использования математического аппарата квантовой механики часто проводят рассмотрение нескольких видов идеализированных «мысленных экспериментов».
Их цель – показать, что принцип не вносит в теорию внутренних противоречий (его справедливость таким способом доказана быть не может).
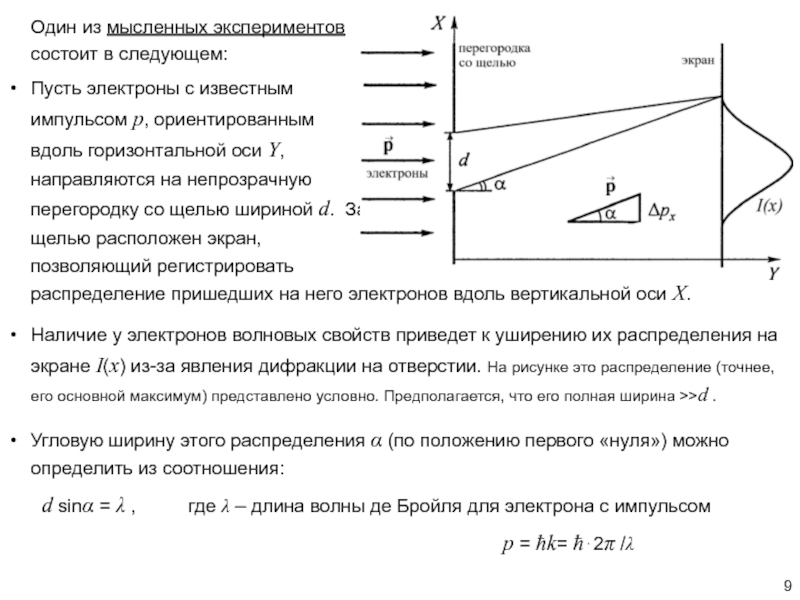
Слайд 9Один из мысленных экспериментов состоит в следующем:
Пусть электроны с известным
импульсом p, ориентированным вдоль горизонтальной оси Y, направляются на непрозрачную
перегородку со щелью шириной d. За щелью расположен экран, позволяющий регистрировать
распределение пришедших на него электронов вдоль вертикальной оси X.
Наличие у электронов волновых свойств приведет к уширению их распределения на экране I(x) из-за явления дифракции на отверстии. На рисунке это распределение (точнее, его основной максимум) представлено условно. Предполагается, что его полная ширина >>d .
Угловую ширину этого распределения (по положению первого «нуля») можно определить из соотношения:
d sin = , где – длина волны де Бройля для электрона с импульсом
p = ħk= ħ2 /
Слайд 10Рассматривая электроны как частицы, мы можем трактовать их отклонение от
центра экрана как свидетельство получения ими вертикальной составляющей импульса, отсутствовавшей
у них до прохождения щели.
Величина этой составляющей различна у различных электронов, ее
неопределенность (ширина статистического распределения) за щелью составляет:
px=psin .
Факт прохождения электрона через щель позволяет считать, что неопределенность его вертикальной координаты за щелью составляет x = d .
Комбинируя приведенные формулы, приходим к соотношению, формально совпадающему с соотношением неопределенностей (с заменой неравенства на равенство):
Неопределенность координаты можно уменьшить, сузив щель. Однако при этом увеличится ширина дифракционной картины и, как следствие – величина px.
xpx = 2ħ
Слайд 11Другой мысленный эксперимент, предложенный самим Гейзенбергом:
Рассмотрим возможность измерения координаты (x)
электрона или другой микрочастицы при помощи микроскопа.
Пусть электрон (электроны) движется
перпендикулярно плоскости рисунка. Для определения его координаты x будем использовать монохроматический свет с длиной волны свет с длиной волны .
Рассеянное электроном излучение будем собираться с помощью микроскопа и формировать изображение (дифракционный максимум конечной ширины) в плоскости фокусировки QQ. Здесь окажется излучение, рассеянное электроном под всеми углами в пределах угла , задаваемого апертурой объектива.
Наилучшая возможная точность измерения координаты (пространственное разрешение) x определяется шириной дифракционного максимума и задается известной из оптики формулой:
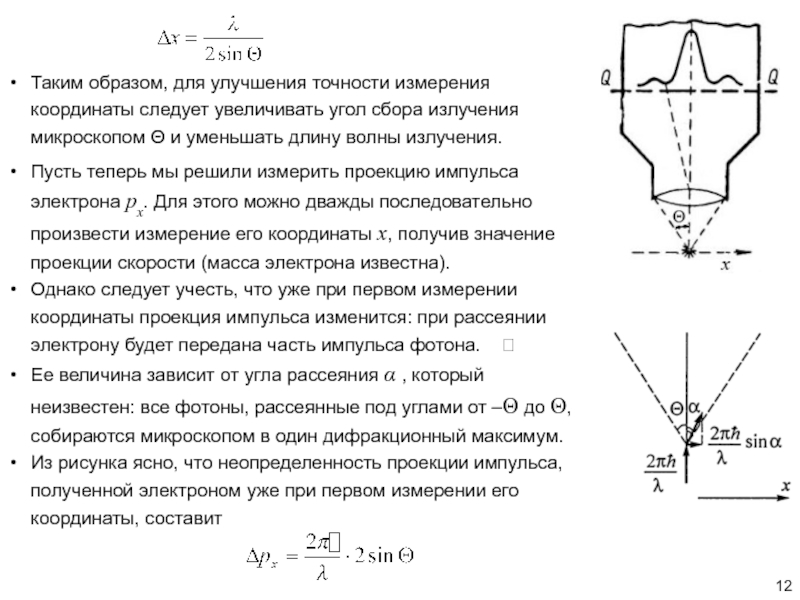
Слайд 12Таким образом, для улучшения точности измерения координаты следует увеличивать угол
сбора излучения микроскопом и уменьшать длину волны излучения.
Пусть
теперь мы решили измерить проекцию импульса электрона px. Для этого можно дважды последовательно произвести измерение его координаты x, получив значение проекции скорости (масса электрона известна).
Однако следует учесть, что уже при первом измерении координаты проекция импульса изменится: при рассеянии электрону будет передана часть импульса фотона.
Ее величина зависит от угла рассеяния , который неизвестен: все фотоны, рассеянные под углами от – до , собираются микроскопом в один дифракционный максимум.
Из рисунка ясно, что неопределенность проекции импульса, полученной электроном уже при первом измерении его координаты, составит
Слайд 13Согласно этой формуле, для улучшения точности измерения проекции импульса следует
уменьшить угол сбора излучения (уменьшить его неопределенность) и увеличить
длину волны излучения.
Таким образом, пути достижения лучшей точности измерений координаты и проекции импульса электрона прямо противоположны.
Нетрудно видеть, что произведение наименьших принципиально достижимых величин погрешности измерений вновь получена соответствует формуле соотношения неопределенностей:
Выполненный Н. Бором (в полемике с Эйнштейном) анализ многих мысленных экспериментов показал, что такая ситуация является всеобщей. При рассмотрении измерений параметров микроскопических объектов нельзя пренебрегать искажениями, вносимыми самим процессом измерений, поскольку они, в силу всеобщей дискретности, не могут быть сделаны бесконечно малыми.
Вместе с тем, эта закономерность не должна рассматриваться в качестве «природного» ограничения самого процесса познания – получения информации о реально существующих характеристиках реальных объектов.
xpx = 2ħ
Слайд 14Как будет показано далее, в квантовой механике многим возможным состояниям
квантовых систем не соответствуют конкретные (точно определенные) значения привычных нам
макроскопических параметров.
Существуют состояния, для которых определены точные значения координат объекта или его импульса. Однако, как оказалось, ни для каких состояний точные значения координат и импульса не определены одновременно.
Таким образом, сами понятия координат и импульса просто не вполне «хороши» (релевантны) для описания микросистем. Состояние системы может быть вполне определенным, но (в отличие от более «интуитивно понятного» идеального объекта – материальной точки) не характеризоваться точными значениями координат и импульса.
При проведении измерений импульса (волнового вектора) и дифракционных экспериментов создают такие условия, что квантовая система оказывается наиболее близкой к состоянию, для которого определенными являются волновые числа (проекции волнового вектора). При этом проявляются волновые свойства микрочастиц, в частности, их способность к дифракции. Траектории частиц, напротив, не могут быть определены.
Чтобы локализовать частицу (например, установить, через какое отверстие она прошла или с каким атомом кристаллической решетки взаимодействовала), требуется внести изменения в схему измерений, направленные на перевод квантовой системы в состояние, для которого лучше определены координаты частиц. При этом точные значения импульсов (волновых чисел) утрачиваются – как в мысленном эксперименте с микроскопом – и дифракционные картины пропадают.

Слайд 15Помимо координат и импульсов, существуют и другие пары сопряженных величин,
которые не могут быть одновременно точно определены. В частности, это
относится к паре энергия-время:
Импульс частицы пропорционален волновому числу волны де Бройля, и поэтому не может быть локализован в пространстве. Точно так же, энергия частицы пропорциональна частоте волны де Бройля, и поэтому не может быть локализована во времени – можно рассмотреть соответствующие волновые пакеты.
Таким образом, точное значение энергии может быть определено лишь для долгоживущих (стационарных, t) состояний квантовых систем.
Для макроскопических объектов принцип (закон) неопределенности не имеет обнаружимых последствий. Поэтому он не был открыт до XX века.
Спектры возможных состояний для них столь «плотны», что «соседние» состояния с определенными величинами координат и импульса близки до неразличимости.
Проведем оценку для тела массой M =1 г =10–3 кг. Пусть его координата определена с точностью x = 1 мкм = 10–6 м. Тогда ограничение, налагаемое соотношением неопределенностей на точность определения его скорости, будет выглядеть как:
v 2ħ / (M x) 6.6210–34 /(10–3 10–6) [м/с] ~ 10–24 [м/с] .
Такая погрешность, очевидно, не могла быть обнаружена на практике.

Слайд 16В своей первой работе (1927 г.), посвященной принципу неопределенности, Гейзенберг
сделал вывод, что «квантовая механика определенно установила несостоятельность принципа причинности».
Этот вывод не вполне верен.
Под принципом причинности понималась концепция «лапласова детерминизма»: положение о том, что если точно задать координаты и импульсы всех частиц (состояние системы), принципиально возможно предсказать ее дальнейшее поведение на сколь угодно долгий срок.
Принцип неопределенности делает невозможным точное определение координат и импульсов в какой-либо момент времени. Следовательно, и предсказание будущих состояний системы кажется невозможным.
В действительности, состояние квантовой системы может быть точно определено – хотя и не через задание координат и импульсов частиц. Возможно и построение решений квантовых задач для всех моментов времени.
Слайд 17Итого:
Принцип неопределенности Гейзенберга представляет собой фундаментальный закон природы.
Он устанавливает границы
возможности использования применительно к микрообъектам классических представлений о частицах как
о материальных точках, состояние которых исчерпывающе характеризуется заданием координат и импульсов.
При этом он никак не раскрывает законов, которые могли бы быть использованы за этими границами. Эта задача решается квантовой механикой.