7. РЕШЕНИЕ ОДУ

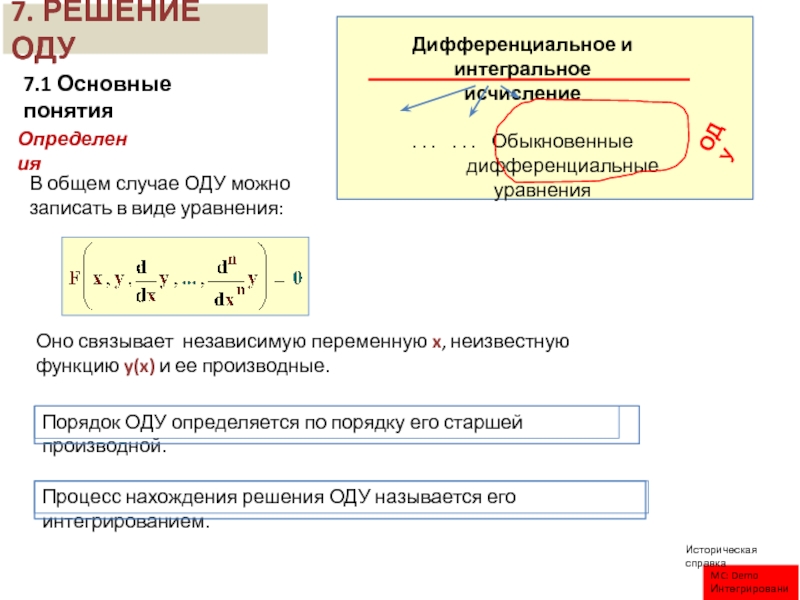
. Обыкновенные
дифференциальные
уравнения
MC: Demo
Интегрирование
Определения
ОДУ
В общем случае ОДУ можно записать в

виде уравнения:

Оно связывает независимую переменную x, неизвестную функцию y(x) и ее производные.

Историческая справка

вида:

определена и непрерывна в некоторой области D .
MC: Demo
Поле направлений
касательная
Поле
направлений

конкретную инт. кривую?

одно (частное) решение можно задать некоторую точку (x0, y0) и

выбрать интегральную кривую, проходящую через эту точку,
т.е. надо задать дополнительное условие
y(x0) = y0 .

Это условие называется начальным условием.


Задача интегрирования уравнения
с заданными начальными условиями
называется начальной задачей или задачей Коши.

решение, д.б. равно порядку уравнения или системы уравнений.
Поэтому для уравнения

2-го порядка задача Коши будет:

2 условия

Для системы n- го порядка:

где

n условий

при x = x0.

Однако, во многих случаях дополнительные условия могут

задаваться в разных точках по x. Такие условия называются ГРАНИЧНЫМИ, а сами задачи – КРАЕВЫМИ ЗАДАЧАМИ.

Очевидно, что краевые задачи возможны для ОДУ или системы ОДУ, начиная со второго порядка.

Пример. Уравнение 2-го порядка

геометрический
смысл

рассмотрим только стандартную функцию Odesolve
функция Odesolve
Предназначена для решения начальных и

краевых задач.

В общем случае имеет следующую структуру:

Odesolve ( [ V ], x, b, [ npoints] )

[ V ] – (необязательный параметр, используется только при решении систем ОДУ) – вектор-функция с именами интегрируемых функций в системе уравнений;
x – имя переменной интегрирования;
b – конечная точка интегрирования;
[ npoints] - целое число узлов, используемых при сплайн - интерполяции полученного решения. Необязательный параметр. По умолчанию - 1000.

с помощью функции Odesolve>

служебное
слово
начальные или
граничные
условия
Примечания:
уравнения должны быть линейны относительно

старшей производной;
количество дополнительных условий должно совпадать с порядком уравнения;
при записи уравнений и дополнительных условий используются булевы операторы;
функция Odesolve возвращает решение в виде функции, полученной сплайн-интерполяцией численных результатов.

кавычек
(набираются Ctrl + F7 )
MC: Demo
Задача1

заданные параметры. Уравнение описывает тот же процесс.
MC: Demo
Задача2

Провести их параметрическое исследование;

Построить поле направлений для уравнения

Решить задачу Коши для этого уравнения при следующих начальных данных:

Решить задачу Коши



Здесь - малый параметр. Получить решения при и . Объяснить влияние на решение.

куда, найди то – не зная что! "
Корректность задачи Коши

для уравнения

Условие существования решения
Если точка (x0,y0) принадлежит некоторой области D на плоскости x,y и в этой области правая часть уравнения f(x,y) определена и непрерывна, то в данной области з.Коши имеет решение.

Условие устойчивости по начальным данным
Если в области D функция f(x,y) удовлетворяет условиям существования и единственности решения, то решение з. Коши непрерывно зависит от правой части уравнения f(x,y) и от точки (x0,y0) .

проходят через каждую точку области D.
D
D
D
интегральные кривые не пересекаются.
малые изменения

начальных данных приводят к малым изменениям решения.

(1) можно представить в интегральной форме:
(2)
эквивалентные
формы
разностная сетка
Разобьем отрезок [x0, xk]

на n малых интервалов – получим последовательность или СЕТКУ значений xi:

узлы сетки

Шаг сетки: hi = xi+1 – xi
- в общем случае м.б. переменной, но обязательно конечной величиной.

y(xi), причем в узле x0 решение y0 известно.

Рассмотрим (2):

Для одного

интервала сетки [xi, xi+1] оно примет вид:

(2)

(2)

неизвестно

Мы будем использовать однопараметрическую аппроксимацию подынтегральной функции f(x,y) на интервале [xi, xi+1] :

(4)

Здесь - известный параметр.

(3)

– шаг разностной сетки.
Явные и неявные разностные схемы
Схема Эйлера
При

из (5) получим схему Эйлера

(6)

Это простейшая схема явного типа
(уравнение явно относительно yi+1).

Геометрический смысл: разностное решение – ломаная линия (касательные)

получим полностью неявную схему
(7)
искомое решение входит
в обе части уравнения
В общем

случае при получим семейство неявных разностных схем. В неявных схемах искомое значение yi+1 входит в обе части разностного уравнения. Такие схемы называются НЕЯВНЫМИ.

Их решение является более сложным, чем явных уравнений. Однако, они обладают свойством повышенной устойчивости при решении особого класса ОДУ – «жестких» дифференциальных уравнений.

Например, при получим неявную схему

(8)

т.е. результат получается с погрешностью. Это вызвано тем, что

дифференциальные уравнения при решении заменяются их разностными аналогами. Поэтому для всех разностных схем проводится оценка их погрешности.

Без вывода

Схема Эйлера

Неявная схема

Неявная схема

error = C h

error = C h2

оценка точности
по порядку h

Здесь С – некоторая константа, зависящая от свойств функции f(x,y)

На практике обычно используют схемы 4 – 5 порядка точности, например, методы Рунге-Кутта.

интегрирования задачи Коши :




Провести тестирование Ваше функции на известном решении.

Решить

уравнение

на интервале
t  [0, tk] ,
где tk - заданный параметр. Предварительно построить поле направлений и провести качественный анализ решения.

Решить систему уравнений
на интервале t  [0, tk] .
Здесь a, b, l, k – параметры задачи.
Провести параметрическое исследование.
Рассмотреть решение на фазовой плоскости.

времени t0=0 найден еще “теплый” труп. Его температура – T0.

Через некоторое время (t=t1) его температура снизилась до T1. Температура окружающего воздуха известна - . Определить момент совершения преступления.

РЕШЕНИЕ:
Построение математической модели.

Согласно законам теплообмена тела с окружающей средой, температура тела описывается уравнением

коэффициент теплообмена

Примем допущения:
1. k = const (не зависит от температуры);
2. Температура окружающей среды не меняется, т.е. =const.

параметра:
 - температура среды (известен);
k - коэффициент теплообмена

(неизвестен).

Найдем k ,используя дополнительное условие T=T1 при t=t1. Для этого проведем серию расчетов при различных k.
Подбором найдем такое значение k, при котором интегральная кривая, выйдя из т. (t0, T0) попадет в т. (t1, T1) .
Это т.н. метод «стрельб».

– в область t

= 30o C; t = 0;
T1 = 28o C; t = 1 (час);
 = 21o C;