Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Relational Data Structure
Содержание
- 1. Relational Data Structure
- 2. CONTENTRelation in mathematicsRelation definition Domains, attributes, schemas
- 3. Nonformal introduction to relationsForm of representation:As a
- 4. Relation definitionLet’s given sets D1, D2,…, Dn
- 5. Additional terms- Sets D1, D2,…, Dn are
- 6. Representation of binary relationsAs a matrix
- 7. Basic operations Union: R ∪ S = {t
- 8. Property of binary relationsReflexivity: Relation R is
- 9. Examples of binary relationsRelation Look-Like(x,y) is reflexive
- 10. Schema of a relationIn mathematics order of
- 11. Property of attributes and schemas Properties of
- 12. Relation instanceRelation instance corresponds to the relation
- 13. Relational data structureThe relational schema and its
- 14. Relations and tables ID1, 2,
- 15. Term correspondenceFormal term Nonformal equivalentdomain allowed values attribute column, field
- 16. KeysThe key is a set of relation
- 17. Simple and compound keysThe key is simple,
- 18. Redundant and minimal keysCompound key is redundant
- 19. Primary keyA relation may have many
- 20. Properties of a primary keyMain properties (integrity
- 21. Example of a primary keyPrimary keyTeachers: No
- 22. Foreign keyIn a relational model relationships between
- 23. Example of a foreign key
- 24. Property of foreign keyMain property (integrity constraint):Value
- 25. Supporting referential constraint Manipulating by tuples of
- 26. Supporting referential integrity constraints in SQLSupporting referential
- 27. Supporting referential constraint – RESTRICTFac-ty No
- 28. Supporting referential constraint – CASCADEFac-ty No
- 29. Supporting referential constraint – SET NULLFac-ty
- 30. Supporting referential constraint – SET DEFAULTFac-ty
- 31. Recursive foreign keyForeign key is recursive if
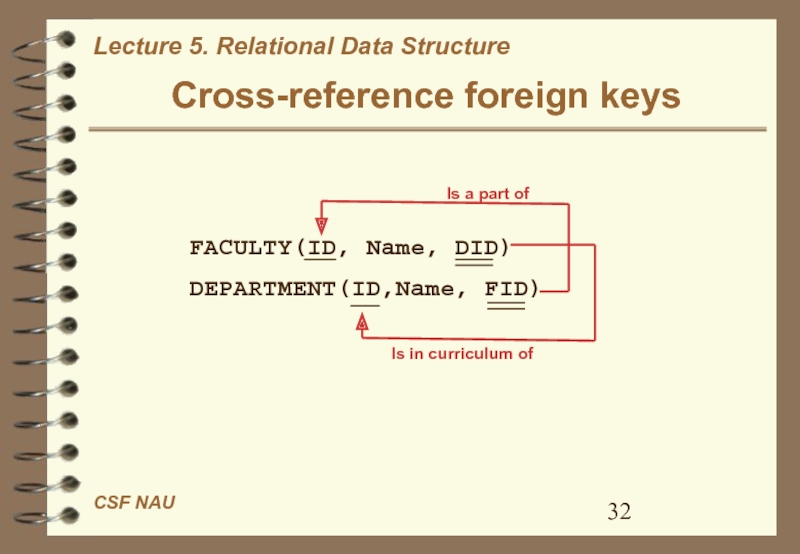
- 32. Cross-reference foreign keysFACULTY(ID, Name, DID)DEPARTMENT(ID,Name, FID)Is a part ofIs in curriculum of
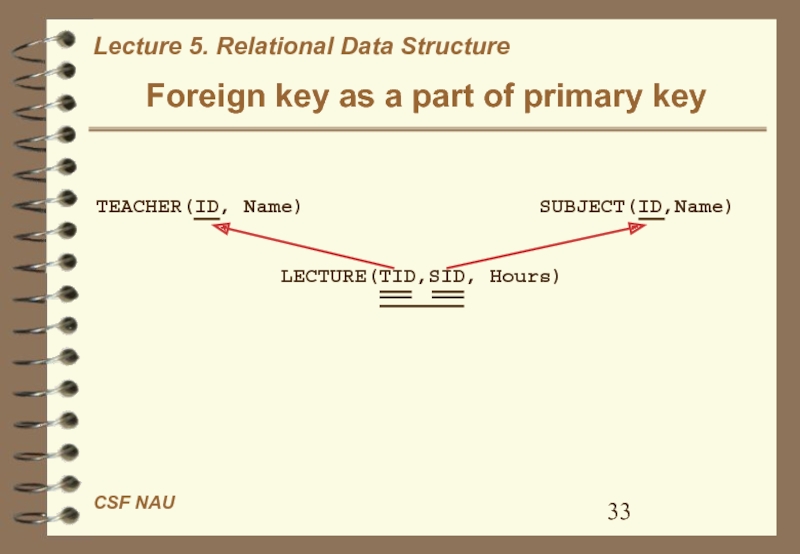
- 33. Foreign key as a part of primary
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Lecture 5. Relational Data Structure
National Aviation University
Computer Science Faculty
Department of
Software Engineering
Слайд 2CONTENT
Relation in mathematics
Relation definition
Domains, attributes, schemas and instances of
relations in RDM
Relations and tables
Keys of relations
Слайд 3Nonformal introduction to relations
Form of representation:
As a table
By using a
condition
Relation is an association between any number of entities.
Like subject
Is more Supply
Who What First Second Who Whom What Q-tyJohn DBMS 5 3 П1 К7 table 200
Peter С 17 5 П3 К14 door 150
Ann XML 2 1 П18 К9 window 1000
Слайд 4Relation definition
Let’s given sets D1, D2,…, Dn (does not obligatory
distinct). Relation R, defined on these sets, is a set
of ordered n-tuples (d1, d2,…, dn), such that d1 ∈ D1, …, dn ∈ DnLets given sets D1, D2,…, Dn (does not obligatory distinct). Cartesian product of these sets, denoted as D1 × D2 ×…× Dn, is a set of all possible tuples (d1, d2,…, dn), such that di ∈ Di, i = 1,n.
R is a relation on the sets D1, D2,…, Dn, if:
R ⊆ D1 × D2 ×…× Dn = {(d1, d2,…, dn) ⏐ di ∈ Di, i = 1,2,…,n}
Слайд 5
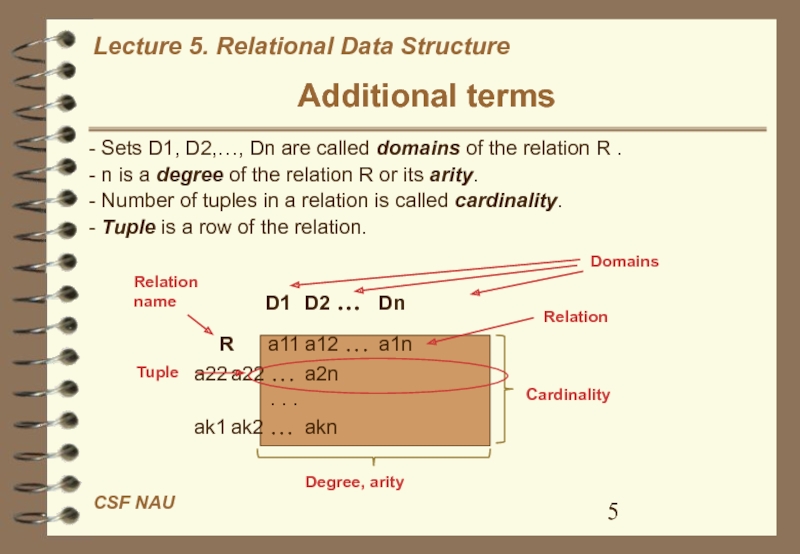
Additional terms
- Sets D1, D2,…, Dn are called domains of
the relation R .
- n is a degree of
the relation R or its arity.- Number of tuples in a relation is called cardinality.
- Tuple is a row of the relation.
D1 D2 … Dn
R a11 a12 … a1n
a22 a22 … a2n
. . .
ak1 ak2 … akn
Domains
Degree, arity
Cardinality
Relation name
Relation
Tuple
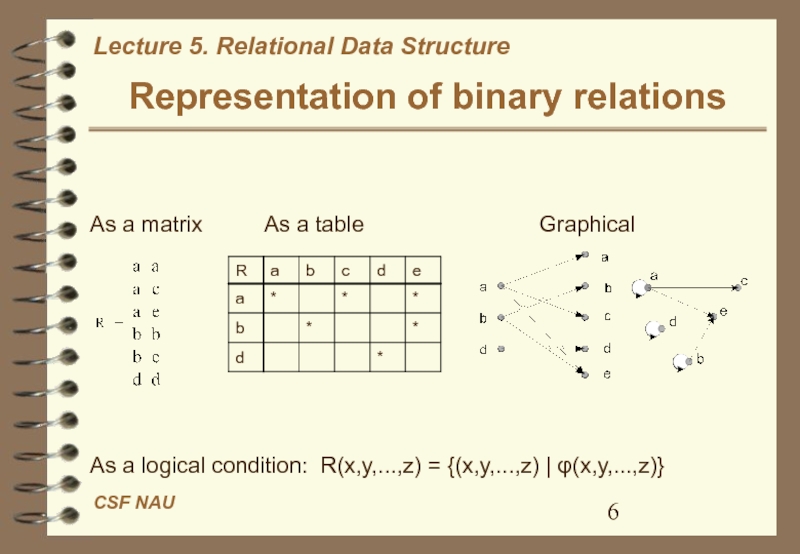
Слайд 6Representation of binary relations
As a matrix
As a table
GraphicalAs a logical condition: R(x,y,...,z) = {(x,y,...,z) | φ(x,y,...,z)}
Слайд 7Basic operations
Union: R ∪ S = {t | t ∈
R ∨ t ∈ S}
Intersection: R ∩ S = {t
| t ∈ R & t ∈ S}Negation: ¬R = {t | t ∉ R}
Cartesian product: R × S = {(r,s) | r ∈ R & s ∈ S }
Слайд 8Property of binary relations
Reflexivity: Relation R is reflexive if:
∀a R(a,
a).
Symmetry: Relation R is symmetric if
∀a∀b (R(a, b) ⇒
R(b, a))Transitivity: Relation R transitive if: ∀a∀b∀с (R(a, b) & R(b, с) ⇒ R(a, c)).
Antisymmetry: Relation R is antisymmetric if:
∀a∀b (R(a, b) & R(b, a) ⇒ a = b).
Слайд 9Examples of binary relations
Relation Look-Like(x,y) is reflexive (any person looks
like himself), symmetric (if b looks like d, then d
looks like b), but not transitive (if have chain of pairs of similar persons it does not mean that persons at the ends of this chain are similar).Relation Is-Higher(x,y) is transitive but not reflexive and symmetric.
Relation Is-Equal (=) is reflexive, symmetric and transitive.
Relation Teach(x,y) is not reflexive, symmetric and transitive.
Слайд 10Schema of a relation
In mathematics order of columns is essential.
Is More
Is More 5 3 3 5 17 5 5 17In relational data structure order of “columns” is not essential. It is achieved at the expense of introducing of the concept “attribute”.
Attribute – is semantically sensible names of the relation columns.
Слайд 11Property of attributes and schemas
Properties of the relation attributes:
Each
attribute of a relation has a name.
The set of allowed
values for each attribute is called the domain of the attribute. Different attributes may have the same domain.
Attribute values are required to be atomic, that is, indivisible.
Properties of the relation schema:
Every schema has a name.
Attribute names in schema must be unique.
Order of attributes in schema is not fixed
Слайд 12Relation instance
Relation instance corresponds to the relation in mathematics with
the only difference – the order of columns in the
relation is not important.Properties of a relation instance:
Order of attributes is arbitrary, but it is defined by a relation schema.
Order of tuples is arbitrary
(tuples may be located in an arbitrary order)
Tuples must be unique within the instance
Слайд 13Relational data structure
The relational schema and its instance have the
following properties:
Name of the relations in relational schema must be
unique As relational structure the set of the relational schema and its instance (state).
The relational schema is a set of the schemas of relations: R1(A1,…,An)
R2(B1,…,Bk)
…
Rn(K1,…,Km)
Instance of relational schema is a set of instances of the relations in
relational schema .
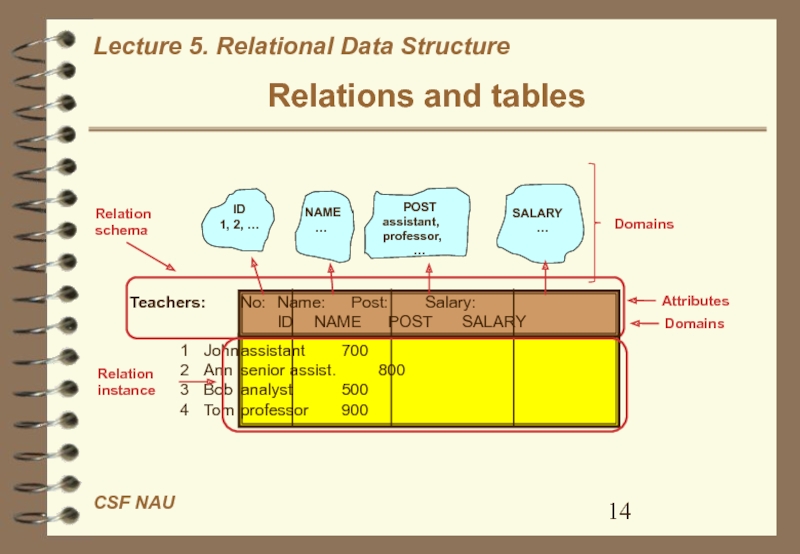
Слайд 14Relations and tables
ID
1, 2, …
POST
assistant,
professor,
…
Domains
NAME
…
SALARY…
Teachers: No: Name: Post: Salary:
ID NAME POST SALARY
1 John assistant 700
2 Ann senior assist. 800
3 Bob analyst 500
4 Tom professor 900
Attributes
Relation schema
Relation instance
Domains
Слайд 15
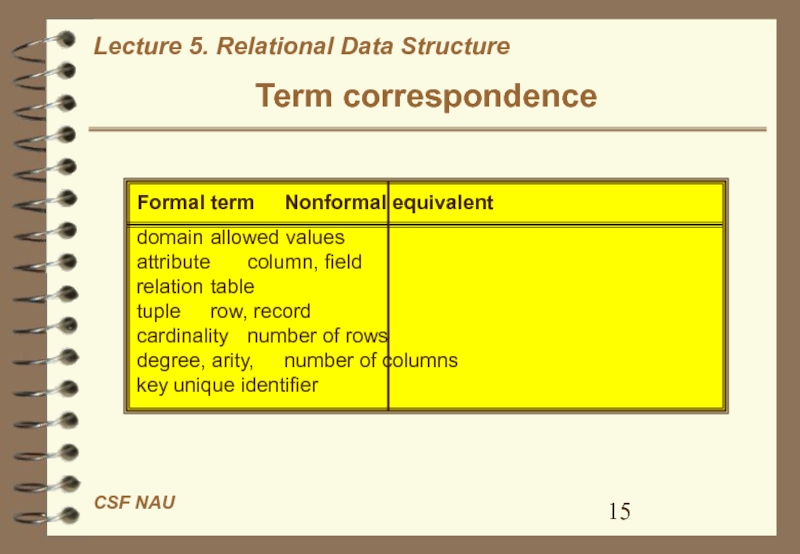
Term correspondence
Formal term Nonformal equivalent
domain allowed values
attribute column, field
relation table
tuple row, record
cardinality number of rows
degree, arity, number
of columns
key unique identifier
Слайд 16Keys
The key is a set of relation attributes that uniquely
identify the tuples of the relation.
Assertion. Any relation has a
key.Example: In the relation STUDENT(No, Name, Course) set of attributes (No, Name, Course) are key because tuples of any relation are unique.
Assertion. Any relation may has many keys.
Слайд 17Simple and compound keys
The key is simple, if it consists
of one attribute.
The key compound if it consists of several
attributes.Example. In the relation:
STUDENT(ID-No, Name, Pasp-ser, Pasp-No, Course)
ID-No is a simple key and pair of attributes
(Pasp-ser, Pasp-No) is a compound key.
Слайд 18Redundant and minimal keys
Compound key is redundant (not minimal) if
there is a subset of this key that is also
a key. Redundant key is also called superkey.Example. In the relation:
STUDENT(ID-No, Name, Pasp-ser, Pasp-No, Course)
key (Pasp-ser, Pasp-No, Course) is redundant key because its subset (Pasp-ser, Pasp-No, Course) is also a key
Nonredundant key is called minimal.
Слайд 19 Primary key
A relation may have many minimal keys. All
of them are called candidate keys.
Example. Relation:
STUDENT (ID-No, Name, Pasp-ser,
Pasp-No, Course)
has two minimal (that is why candidate) keys: ID-No
Pasp-ser, Pasp-No
Among set of all candidate (minimal) keys only one is selected as a primary key.
Слайд 20Properties of a primary key
Main properties (integrity constraints):
Primary key values
must never be duplicated. That is they are unique within
a relation. But there may be duplicates in parts of compound primary key.Primary key cannot have NULL values.
Additional properties:
Every relation must have one and only one primary key.
Primary key do not influence attribute order.
Primary keys do not influence tuple order.
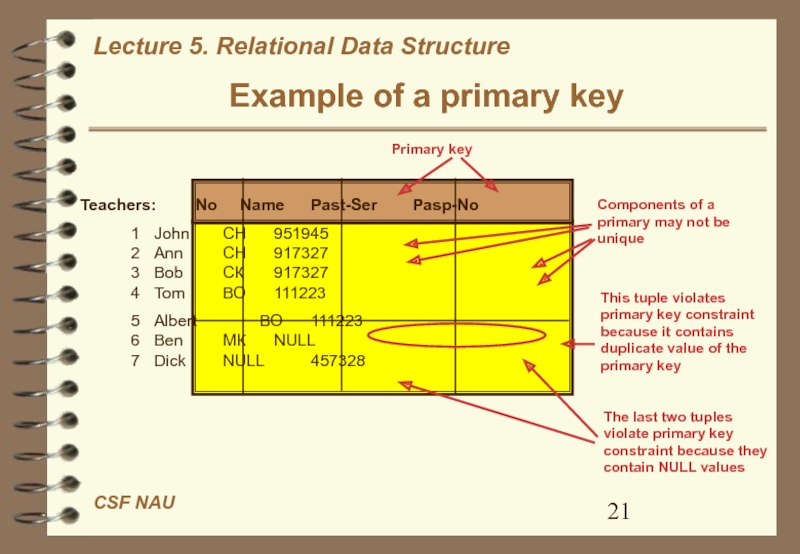
Слайд 21Example of a primary key
Primary key
Teachers: No Name
Past-Ser Pasp-No
1 John СН
951945
2 Ann СН 917327
3 Bob СК 917327
4 Tom ВО 1112235 Albert ВО 111223 6 Ben МК NULL 7 Dick NULL 457328
Components of a primary may not be unique
This tuple violates primary key constraint because it contains duplicate value of the primary key
The last two tuples violate primary key constraint because they contain NULL values
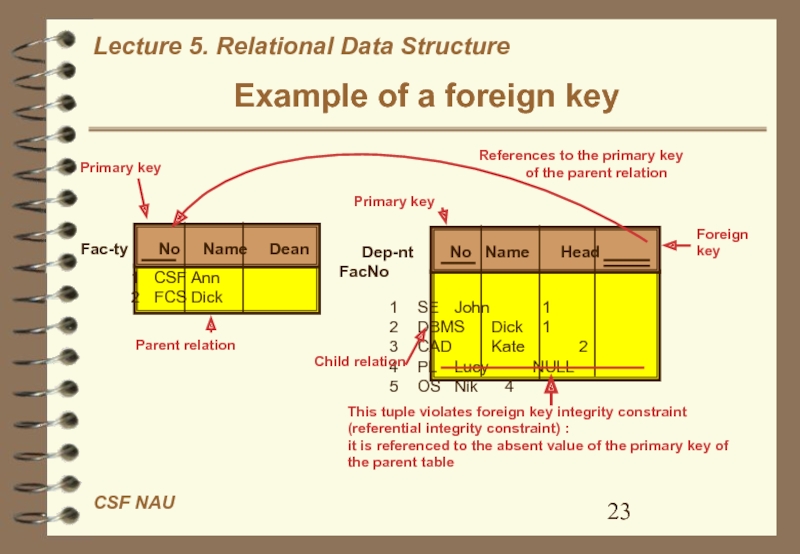
Слайд 22Foreign key
In a relational model relationships between relations are defined
“by values”.
Foreign key is one or more attributes of a
relation that are used to reference to tuples of other relation.Relation that is references to other relation is called child relation.
Relation that is referenced by other relation is called parent relation.
Child relation may references only to primary key (or unique key) of the parent relation.
Слайд 24Property of foreign key
Main property (integrity constraint):
Value of a foreign
key cannot reference to absent values of the primary key
of the parent relation. It is so called referential integrity constraint of the foreign key.Additional properties:
Foreign key can contain duplicate values.
Foreign key can contain NULL values.
Слайд 25Supporting referential constraint
Manipulating by tuples of a child relation:
When
a tuple is added or updated referential constraint is tested
and if it is violated the corresponding action (adding/updating) is rejected.When a tuple is deleted referential constraint cannot be violated.
Manipulating by tuples of a parent relation :
When a tuple is added referential constraint cannot be violated.
When deleting of updating:
Tuple deleting/updating is not done if there are references from child relation, that violate referential integrity constraint.
Deleting/updating tuple of parent relation causes deleting/updating tuples of a child relation that references the tuple of the parent relation.
Deleting/updating tuple of parent relation causes setting NULL values to corresponding tuples of a child relation .
Deleting/updating tuple of parent relation causes setting DEFAULT values to corresponding tuples of a child relation.
Слайд 26Supporting referential integrity constraints in SQL
Supporting referential integrity constraints in
standard SQL:
ON DELETE {RESTRICT | CASCADE | SET NULL |
SET DEFAULT}ON UPDATE {RESTRICT | CASCADE | SET NULL | SET DEFAULT}
Supporting referential integrity constraints in SQL Oracle:
[ON DELETE {CASCADE | SET NULL}]
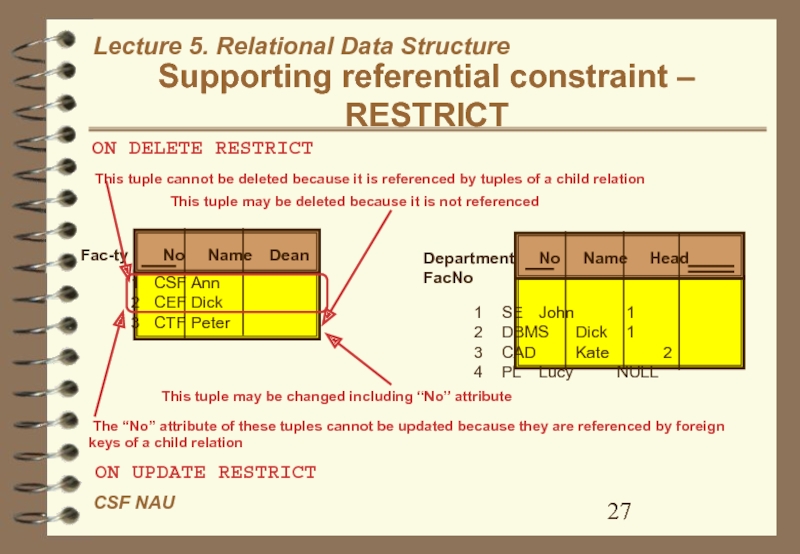
Слайд 27Supporting referential constraint –
RESTRICT
Fac-ty No Name Dean
1 CSF Ann
2 CEF Dick
3 CTF Peter
Department No
Name Head FacNo1 SE John 1 2 DBMS Dick 1 3 CAD Kate 2 4 PL Lucy NULL
ON DELETE RESTRICT
This tuple cannot be deleted because it is referenced by tuples of a child relation
This tuple may be deleted because it is not referenced
ON UPDATE RESTRICT
The “No” attribute of these tuples cannot be updated because they are referenced by foreign keys of a child relation
This tuple may be changed including “No” attribute
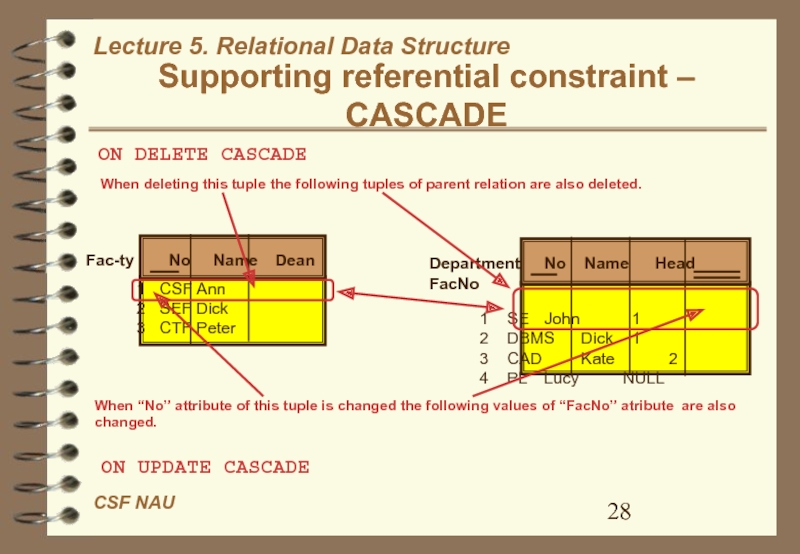
Слайд 28Supporting referential constraint –
CASCADE
Fac-ty No Name Dean
1 CSF Ann
2 SEF Dick
3 CTF Peter
Department No Name
Head FacNo1 SE John 1 2 DBMS Dick 1 3 CAD Kate 2 4 PL Lucy NULL
ON DELETE CASCADE
When deleting this tuple the following tuples of parent relation are also deleted.
ON UPDATE CASCADE
When “No” attribute of this tuple is changed the following values of “FacNo” atribute are also changed.
Слайд 29Supporting referential constraint –
SET NULL
Fac-ty No Name
Dean
1 CSF Ann
2 SEF Dick
3 CTF Peter
Department No
Name Head FacNo1 SE John 1 2 DBMS Dick 1 3 CAD Kate 2 4 PL Lucy NULL
ON DELETE SET NULL
On deleting this tuple the following values of “FacNo” attribute are set to NULL.
ON UPDATE SET NULL
When “No” attribute of this tuple is changed the following values of “FacNo” atribute are set to NULL.
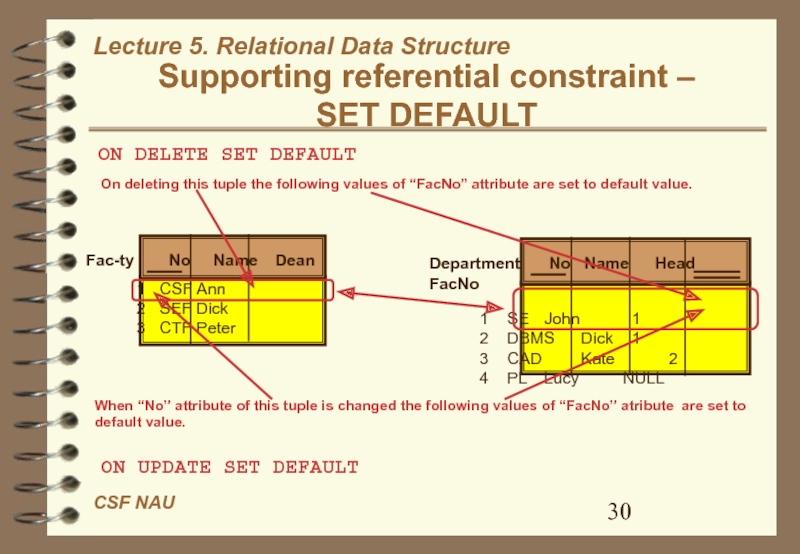
Слайд 30Supporting referential constraint –
SET DEFAULT
Fac-ty No Name
Dean
1 CSF Ann
2 SEF Dick
3 CTF Peter
Department No
Name Head FacNo1 SE John 1 2 DBMS Dick 1 3 CAD Kate 2 4 PL Lucy NULL
ON DELETE SET DEFAULT
On deleting this tuple the following values of “FacNo” attribute are set to default value.
ON UPDATE SET DEFAULT
When “No” attribute of this tuple is changed the following values of “FacNo” atribute are set to default value.
Слайд 31Recursive foreign key
Foreign key is recursive if it references to
the primary key of the relation where it is defined.
Teacher No Name Pasp-Ser Pasp-No ChiefNo
1 Ann СН 951945 4 2 Dick СН 917327 4 3 Peter СК 917327 7 4 John ВО 111223 7 5 Kate ВО 111224 4 6 Lucy МК NULL 7 7 Mary NULL 457328 NULL
It allows to model hierarchy structure that is defined on one relation.