Алгебра логики

правильно рассуждать, делать выводы, доказывать утверждения.
Формальная логика отвлекается от конкретного

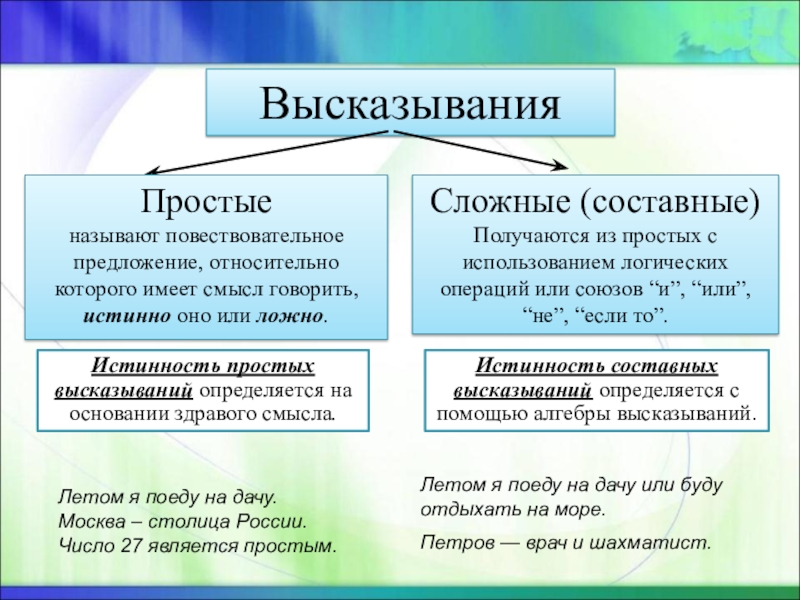
Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно.

изобретен в середине XIX века».
Какие из предложений являются высказываниями? Какие

1. Какой длины эта лента? 2. Прослушайте сообщение. 3. Делайте утреннюю зарядку! 4. Назовите устройства ввода информации. 5. Кто отсутствует? 6. Париж – столица Англии. 7. Число 11 является простым. 8. 4+5=10 9. Без труда не вытащишь и рыбку из пруда. 10. Сложите числа 2 и 5. 11. Некоторые медведи живут на Севере. 12. Все медведи – бурые. 13. Чему равно расстояние от Москвы до Ленинграда? 14. Сумма углов треугольника – 180 градусов.
15. В городе N живут 2 миллиона человек.

высказываниями или над объектами, которые могут принимать только два значения

В 1842 году английский математик Джорж Буль разработал математическую логику или алгебру логики, которую впоследствии стали называть «булевой алгеброй».
Спустя 100 лет алгебра логики стала основой теории цифровых вычислительных машин, ее используют в компьютерной логике, электронике, в основе всех микропроцессорных операций.

или ложность составных высказываний, не вникая в их содержание

или ложно.
Сложные (составные)
Получаются из простых с использованием логических операций

Летом я поеду на дачу.
Москва – столица России. Число 27 является простым.

Летом я поеду на дачу или буду отдыхать на море.
Петров — врач и шахматист.

Истинность простых высказываний определяется на основании здравого смысла.

Истинность составных высказываний определяется с помощью алгебры высказываний.

Обозначаются буквами латинского алфавита: A, B, C…
Логические переменные могут принимать

Например, два простых высказывания:
А = «2  2 = 4» истина (1)
В = «2  2 = 5» ложь (0)
являются логическими переменными А и В

определенные логические операции, в результате которых получаются новые высказывания

«НЕ»)
Импликация (логическое следование, «Если А, то В»)
Эквивалентность (логическое равенство (тождество),

«И» называется операцией логического умножения, или конъюнкцией.

является истинным тогда и только тогда, когда истинны все входящие

Таблица истинности функции логического умножения

В переводе на естественный язык «и А, и В» «как А, так и В» «А вместе с В» «А несмотря на В» «А, в то время как В»

И , , and, &, *, ·

Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 кратно 2» = ИСТИНА А и В – «Число 10 – четное и отрицательное» - ЛОЖЬ А и С – «Число 10 как четное, так и кратно 2» - ИСТИНА

0

«ИЛИ» называется операцией логического сложения, или дизъюнкцией.

является истинным тогда, когда истинно хотя бы одно из входящих

В переводе на естественный язык «А или В»

Таблица истинности функции логического сложения

Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ А или В – «Число 10 – четное или отрицательное» - ИСТИНА А или С – «Число 10 четное или простое» - ИСТИНА В или С – «Число 10 отрицательное или простое» - ЛОЖЬ

ИЛИ, , or, +, |

инверсией.

истинное высказывание ложным и, наоборот, ложное – истинным.
Таблица истинности функции

Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Луна – спутник Земли» = ИСТИНА
Не А – «Неверно, что число 10 – четное» = ЛОЖЬ
Не В – «Неверно, что число 10 – отрицательное» = ИСТИНА
Не С – «Неверно, что Луна – спутник Земли» = ЛОЖЬ

В переводе на естественный язык «Не А» «Неверно, что А»

НЕ, NOT, ¬,

помощью оборота речи «если …, то …».

только тогда, когда из истины следует ложь.
От лат. implicatio –

Таблица истинности функции логического следования

→, , , IMP

В переводе на естественный язык «если А, то В» «В, если А» «Когда А, тогда В» «А достаточно для В» «А только тогда, когда В»

Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ А В – «Если число 10 – четное, то оно - отрицательное» - ЛОЖЬ А С – «Число 10 простое, если четное» -ЛОЖЬ «Если число делится на 10, то оно делится на 5» ИСТИНА

помощью оборота речи «… тогда и только тогда, когда …».

только тогда, когда оба высказывания одновременно либо истинны, либо ложны.
От

Таблица истинности функции логического равенства

В переводе на естественный язык «А эквивалентно В» «А только тогда и только тогда, когда В»

, , , , EQV

Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ А В – «Число 10 – четное, тогда и только тогда, когда оно - отрицательное» - ЛОЖЬ В С – «Число 10 такое же простое, как и отрицательное» ИСТИНА

приближенная к грамматической конструкции «либо … либо …».

один из битов a или b равен 1 (единице), во

Таблица истинности функции исключающее ИЛИ

Пример: Даны высказывания
А – «Я пойду в кино» = ИСТИНА
В – «Я пойду на каток» = ИСТИНА
С – «Я пойду в школу» = ЛОЖЬ
А  В – «Я пойду либо в кино либо на каток» - ЛОЖЬ А  С – «Я пойду либо в кино либо в школу» - ИСТИНА В  С – «Я пойду либо на каток либо в школу» - ИСТИНА

, XOR

логических выражений
«Летом Петя поедет в деревню и, если будет хорошая

1

А

В

С

F=A * (B C)

2

(X>=A) * (X<=B)

«Точка Х не принадлежит интервалу [A;B]»

3

(X>=A) * (X<=B)

«Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя.»

4

В

С

D – идет дождь

В (С D)

Упражнения по записи высказываний в виде логических выражений
«Если урок будет

5

У

М

В

С

Урок будет интересным

Миша будет смотреть в окно

Вика будет смотреть в окно

Света будет смотреть в окно

У М*В*С

«Я пойду гулять тогда и только тогда, когда выучу все уроки.»

6

В

С