Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра логики. Основные логические операции 10-11 класс
Содержание
- 1. Алгебра логики. Основные логические операции 10-11 класс
- 2. Развить математический стиль мышления.Изучить логические принцип работы компьютераВоспитание информационной культуры.Цели:
- 3. Логика, ее разделыЛогические операцииЛогические схемыТриггерРегистр, счетчик, сумматорЗаключениеСОДЕРЖАНИЕ
- 4. В 1847 г. английский математик Джордж Буль
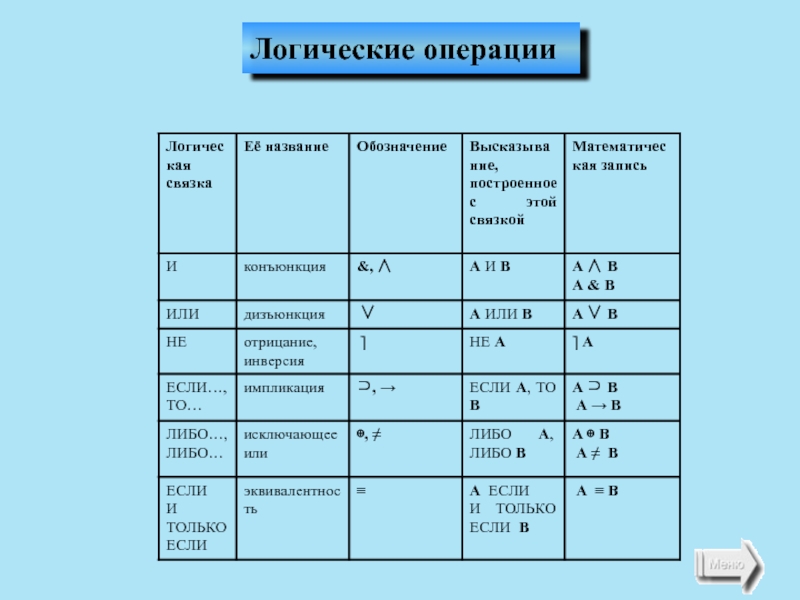
- 5. Логические операции
- 6. В вычислительной технике и автоматике используют логические
- 7. На вход схемы поступает двоичный сигнал, связь
- 8. Схема И (конъюнкция)Реализует операцию логического умножения
- 9. Схема ИЛИ (дизъюнкция)Реализует операцию логического сложения
- 10. Схема ИЛИ-НЕ Реализует операцию отрицания схемы ИЛИ
- 11. Схема И-НЕ Реализует операцию отрицания схемы ИЛИ
- 12. Электронная схема, применяемая в регистрах компьютера для
- 13. Для кратковременного хранения 16 бит информации
- 14. ЗаключениеИтак, логика возникла задолго до появления компьютеров
- 15. БиблиографияБашлы П.Н. Основы информатики. Учебное пособие. –
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Алгебра логики.
Основные логические
операции
10-11 класс
Автор: Красавина И.В.
БУ «Нефтеюганский политехнический
колледж»
Слайд 2Развить математический
стиль мышления.
Изучить логические принцип
работы
компьютера
Воспитание информационной
культуры.
Цели:
Слайд 3Логика, ее разделы
Логические операции
Логические схемы
Триггер
Регистр, счетчик, сумматор
Заключение
СОДЕРЖАНИЕ
Слайд 4
В 1847 г. английский математик Джордж Буль в своей работе
«Математический анализ логики» изложил основы «булевой» алгебры, и его считают
основоположником алгебры логики. Алгебра логики изучает методы установления истинности или ложности высказываний (утверждений). Логический подход заключается в том, что истинность высказываний устанавливается на основании истинности других высказываний, с помощью рассуждений и нахождения противоречий. Основные разделы логики: формальная логика (изучает особенности человеческих
рассуждений);
математическая логика (изучает технику математических теорий и доказательств);
диалектическая логика (изучает закономерности и процессы, происходящие в природе, обществе и сознании);
компьютерная логика (логические закономерности применительно к вычислительной технике).
Джордж Буль
Логика, ее разделы
Слайд 6
В вычислительной технике и автоматике используют логические схемы – устройства,
которые преобразуют двоичные сигналы.
В 50-х годах века американский учёный
Клод Шеннон связал булеву алгебру с двоичной системой кодирования и использовал для анализа и проектирования релейно–контактных схем, принцип работы которых использовался при создании первых электронно-вычислительных машин.Клод Шеннон
Основные логические операции: И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и др., выполняемые над двоичными переменными, реализованы в логических элементах.
Логический элемент – это небольшая часть электронной логической схемы, которая выполняет элементарную логическую операцию.
Логические схемы
Слайд 7
На вход схемы поступает двоичный сигнал, связь между ним и
выходным сигналом выражается с помощью таблиц истинности.
Простая электрическая схема, состоящая
из одного и более ключей (контактов) иллюстрирует работу логической схемы. Значениям 1 и 0 соответствует наличие или отсутствие тока в цепи.Схема НЕ (инвертор)
Реализует операцию отрицания
Таблица истинности
А – входной сигнал, А – выходной сигнал
А А
Условное обозначение схемы
Электрическая схема
Логические схемы
Слайд 8
Схема И (конъюнкция)
Реализует операцию логического умножения
Таблица истинности
А B
А
B
А*B
Условное обозначение схемы
Электрическая схема
Логические схемы
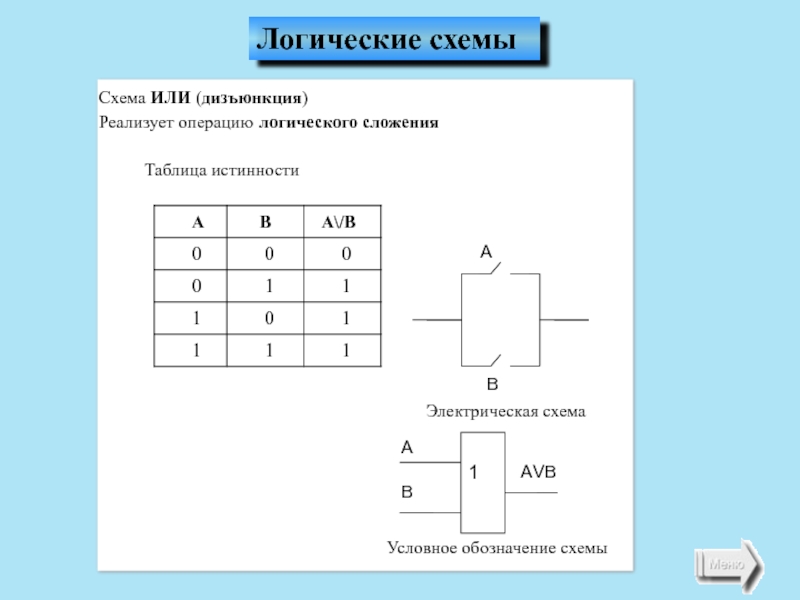
Слайд 9
Схема ИЛИ (дизъюнкция)
Реализует операцию логического сложения
Таблица истинности
А
А
B
АVB
B
Условное обозначение схемы
Электрическая схема
Логические схемы
Слайд 10
Схема ИЛИ-НЕ
Реализует операцию отрицания схемы ИЛИ
Таблица
истинности
А
B
АVB
Условное обозначение схемы
Логические схемы
Слайд 11
Схема И-НЕ
Реализует операцию отрицания схемы ИЛИ
Таблица
истинности
А
B
А*B
Условное обозначение схемы
Логические схемы
Слайд 12
Электронная схема, применяемая в регистрах компьютера для запоминания одного разряда
двоичного кода (бита) – это триггер.
Триггер имеет два устойчивых состояния, которые соответствуют логической «1» и логическому «0». Trigger в переводе с англ. означает защелка, спусковой крючок. Самый распространённый тип RS триггер (Set – установка, Reset - сброс.) состоит из двух схем ИЛИ–НЕ.
Таблица истинности
S
R
Q
Q
Триггер
Слайд 13
Для кратковременного хранения 16 бит информации (2-х байтов или
одного машинного слова) предназначен регистр.
Регистр – совокупность триггеров, число которых
соответствует числу разрядов в слове. В соответствии с типом хранящегося машинного слова регистрам присваиваются наименования. Например, регистр команд, регистр адреса, счетчик и т.д.Счетчик – триггерный регистр. Он может состоять, например, из 4-х триггеров (4-х битный счетчик). При подаче на вход двоичного числа, счетчик увеличивает его на 1.
Шифратор (дешифратор) – схема с несколькими входами и выходами, служащая для преобразования двоичного кода.
Электронная схема, применяемая для суммирования двоичных чисел – сумматор. Он имеет три входа и два выхода.
При сложении двух n – разрядных двоичных кодов складывать приходится цифры кодов и прибавлять ещё цифру – перенос из предшествующего младшего разряда.
Таким образом, в любом разряде при сложении кодов нужно складывать три одноразрядных двоичных числа.
Условное обозначение схемы
Регистр, счетчик, сумматор
Слайд 14
Заключение
Итак, логика возникла задолго до появления компьютеров и возникла она
в результате необходимости в строгом формальном языке. Были построены функции
– удобное средство для построения сложных утверждений и проверки их истинности. Оказалось, что такие функции обладают аналогичными свойствами с алгебраическими операторами. Это дало возможность упрощать исходные выражения. Особое свойство логических выражений – возможность их нахождения по значениям. Это получило широкое распространение в цифровой электронике, где используются логические элементы, и программировании.Слайд 15
Библиография
Башлы П.Н. Основы информатики. Учебное пособие. – Ростов-на-Дону.: Феникс, 2004.
-128с.
Информатика. Базовый курс/ С.В.Симонович и др. – СПб.: Питер, 2000.-640
с.Соболенко Р. Младшая карта бьет старшую//Hard'n'Soft, 2004, №7, с. 68-73.
Кожемяко А. Современные мультиформатные картоводы. Электронная статья. – Режим доступа: http://www.ixbt.com/storage/readers.shtml.
Поляков А. Изучение производительности 5 накопителей с flash-памятью и интерфейсом USB 2.0. Электронная статья. – Режим доступа: http://www.ferra.ru/online/storage/25367.
«Компьютер» Ю. Л. Кетков, изд. «Дрофа» 1997 г.
«Математика» Ю. Владимиров, изд. «Аванта+» 1998 г.