Слайд 1Алгебра
Кабанов Александр Николаевич
к.ф.-м.н., доцент кафедры кибернетики
Слайд 3Корректирующие коды
В идеальной системе при отсутствии искажений в канале символы,
которые появляются на выходе устройства, декодирующего сигналы на выходе канала,
должны совпадать с символами, которые поступают на вход кодера канала.
Однако в реальной системе всегда имеются случайные ошибки.
Для того чтобы обнаруживать и исправлять такие ошибки, нужны корректирующие коды.
Слайд 4Схема системы связи
Кодер, кодирующий входную информацию в двоичные символы.
Кодер, кодирующий
двоичные символы для исправления возможных будущих ошибок.
Модулятор, кодирующий двоичные сигналы
в сигналы на входе в канал.
Канал связи.
Демодулятор, декодирующий сигналы на выходе канала в двоичные символы.
Слайд 5Схема системы связи
Декодер, предназначенный для исправления возможно появившихся ошибок в
двоичных символах.
Декодер, декодирующий двоичные символы в сообщение.
Слайд 6Корректирующие коды
Говорят, что код обнаруживает ошибку, если декодер сигнализирует об
отличии принятой последовательности от переданного кодового слова.
Говорят, что код исправляет
ошибку, если декодер указывает позицию и значение искаженного символа. Для двоичного кода достаточно указать только позицию.
Слайд 7Блоковые коды
При создании блокового кода непрерывная последовательность информационных символов разбивается
на k-значные блоки, т.е. на отрезки, содержащие по k символов.
В дальнейшем все операции проводятся над каждым блоком независимо от других.
К каждому информационному блоку из k символов добавляется набор из r = n – k символов, называемых проверочными.
Набор, состоящий из k информационных и r проверочных символов, называется кодовым словом.
Слайд 8Блоковые коды
Каждое кодовое слово передается по каналу связи, возможно искажается
информационным шумом, а затем декодируется независимо от других кодовых слов.
Величина
k + r = n называется длиной блока.
Совокупность всех кодовых слов называется кодом.
Если мощность кодового алфавита равна m, то этот алфавит можно отождествить с конечным полем Fm.
Слайд 9Канал связи
Для реального канала вероятность совпадения принятого и переданного символа
больше вероятности искажения передаваемого символа (причем для хорошего канала много
больше).
Значит, получение на выходе канала блока без ошибок более вероятно, чем получение блока с одной ошибкой.
А эта вероятность, в свою очередь, больше вероятности появления блока с двумя ошибками и т.д.
Слайд 10Метод максимального правдоподобия
В предположении, что все слова кода имеют одинаковую
вероятность быть переданными по каналу связи, наилучшим решением на приемнике
будет декодирование в такое кодовое слово, которое отличается от полученного в наименьшем числе компонент.
Такое декодирование называется декодирование по методу максимального правдоподобия.
Слайд 11Расстояние Хемминга
Так как символы кодового алфавита можно представить элементами конечного
поля, значит каждое кодовое слово можно отождествить с вектором линейного
пространства над этим полем.
Весом кодового слова g называется величина w(g), равная числу ненулевых координат вектора g.
Расстоянием Хемминга между двумя кодовыми словами g и h называется величина d(g, h) = w(g – h).
Таким образом, расстояние между двумя словами – это число координат, в которых эти слова отличаются друг от друга.
Слайд 12Код, обнаруживающий ошибки
При искажении t компонент кодового слова, переданного по
каналу связи, слово, полученное на выходе канала, будет отличаться от
переданного в t координатах. Другими словами, оно будет удалено от исходного слова на расстояние t.
Лемма 1: Для того, чтобы обнаружить все комбинации из t или меньшего числа ошибок, необходимо и достаточно, чтобы минимальное расстояние Хемминга между кодовыми словами было равно t + 1.
Слайд 13Код, исправляющий ошибки
Лемма 2: Для того, чтобы исправить все комбинации
из t или меньшего числа ошибок, необходимо и достаточно, чтобы
минимальное расстояние Хемминга между кодовыми словами было равно 2t + 1.
Минимальное расстояние Хемминга между всевозможными парами слов кода называется кодовым расстоянием кода.
Слайд 14Линейный код
Пусть Vn – линейное пространство над конечным полем Fm.
Линейным блоковым кодом называется любое подпространство G Vn(Fm).
Величина d
= min{d(g, h}|g, h G, g h} – кодовое расстояние кода G. Так как G – подпространство, значит g, h G g – h = f G.
Следовательно: d = min{d(g, h}|g, h G, g h} =
= min{w(g – h}|g, h G, g h} = min{w(f}|f G, f 0}.
Таким образом, кодовое расстояние для линейного кода равно минимальному весу его ненулевых слов.
Слайд 15Порождающая матрица
Пусть G Vn(Fm) – линейный код размерности k.
Матрица G размера kn, составленная из базисных векторов подпространства G,
называется порождающей матрицей кода G.
Задание кода с помощью порождающей матрицы более компактно. Например, двоичный линейный код размерности 30 с длиной блока 50 содержит 230 > 109 слов и требует как минимум 6,25 ГБ памяти для хранения, но может задаваться порождающей матрицей размера 3050, что требует 187,5 Б памяти.
Слайд 16Проверочная матрица
Векторы g, h Vn называются ортогональными, если их
скалярное произведение равно 0.
Пусть G – линейное подпространство Vn(Fm) размерности
k. Множество всех векторов из Vn, ортогональных всем векторам из G, образует ортогональное линейное подпространство G размерности n – k.
Матрица H, составленная из базисных векторов подпространства G, называется проверочной матрицей линейного кода G.
Подпространство G порождает линейный код, называемый двойственным к коду G.
Слайд 17Проверочная матрица
Вектор g G тогда и только тогда, когда
gHT = 0.
Значит, GHT = 0.
Лемма: Пусть G – линейный
код с проверочной матрицей H. Тогда каждому кодовому слову с весом d соответствует соотношение линейной зависимости, связывающее d столбцов матрицы H. И наоборот, каждому соотношению линейной зависимости, включающему d столбцов матрицы H, соответствует кодовое слово веса d.
Слайд 18Эквивалентные коды
Линейный код с длиной блока n, количеством информационных символов
k и кодовым расстоянием d называется линейным (n,k,d)-кодом.
Линейные коды, отличающиеся
друг от друга перестановкой столбцов в порождающей матрице, называются эквивалентными.
Линейные коды называются комбинаторно-эквивалентными, если порождающую матрицу одного можно получить из порождающей матрицы другого с помощью элементарных преобразований строк и столбцов.
Слайд 19Систематический код
Линейный (n,k,d)-код называется систематическим, если первые k координат каждого
кодового слова являются информационными символами, а последние n – k
координат – проверочными символами.
Теорема: Любой линейный (n,k,d)-код эквивалентен систематическому.
Слайд 20Систематический код
Порождающая матрица систематического (n,k,d)-кода имеет вид:
Слайд 21Систематический код
Теорема: Если G – систематический (n,k,d)-код с порождающей матрицей
G = (Ek|A), где Ek – единичная матрица размера kk,
а А – некоторая матрица размера k(n – k), то проверочная матрица имеет вид H = (–AT|En – k).
Слайд 22Таблица стандартного расположения
Пусть G – линейный (n,k,d)-код. Следующий алгоритм декодирования
слов, полученных на выходе из канала, основан на таблице стандартного
расположения.
Выписать в первую строку таблицы все вектора линейного подпространства G, начиная с нулевого.
Выбрать из пространства Vn вектор h1 минимального веса, не лежащий в коде G, добавить его к каждому кодовому вектору и записать полученные вектора во вторую строку так, чтобы под вектором gi оказался вектор gi + h1. Если таких векторов минимального веса несколько, то выбрать любой из них.
Слайд 23Таблица стандартного расположения
Выбрать из пространства Vn вектор h2 минимального веса,
не лежащий в предыдущих двух строках таблицы, добавить его к
каждому кодовому вектору и записать полученные вектора в третью строку так, чтобы под вектором gi + h1 оказался вектор gi + h2. Если таких векторов минимального веса несколько, то выбрать любой из них.
Повторять аналогичную процедуру из шага 3, пока в таблице не окажутся все вектора пространства Vn.
Найти в таблице полученное на выходе из канала слово f.
Искомое кодовое слово g будет находиться в первой строке того же столбца, где расположено слово f.
Слайд 24Таблица стандартного расположения
Фактически, каждая строка таблицы стандартного расположения представляет собой
смежный класс G + hi = {g + hi|g
G}.
По известной теореме из алгебры, всё линейное пространство распадается на непересекающиеся смежные классы по любому своему фиксированному подпространству.
Это гарантирует нам, что при выборе hi, не лежащего в предыдущих строках, мы будем получать новый смежный класс, не пересекающийся с предыдущими, а также то, что построенная таким образом таблица обязательно будет содержать все вектора линейного пространства.
Слайд 25Вектор ошибок
Если при передаче по каналу слова g на выходе
из канала было получено слово f, то вектор e =
f – g называется вектором ошибок.
Если e = 0, то можно считать, что ошибок при передаче не произошло. Вектор ошибок будет равен 0 и в случае, если произошло n ошибок, но для приемлемого канала связи и достаточно большом n вероятность этого исчезающе мала.
Если e 0, то ненулевые координаты этого вектора соответствуют искажаемым координатам вектора g.
Слайд 26Вектор ошибок
Вектора hi в таблице стандартного расположения называются образующими соответствующих
смежных классов.
Фактически, эти образующие есть вектора ошибок, которые могут произойти
с кодовыми словами при передаче по каналу связи, а слова в соответствующем смежном классе – это кодовые слова, искаженные данным вектором ошибок.
Так как в приемлемом канале меньшее число ошибок более вероятно, чем большее, то для более адекватного декодирования целесообразно выбирать в качестве образующих смежных классов вектора наименьшего возможного веса.
Слайд 27Правильное декодирование
Лемма: При использовании таблицы стандартного расположения полученный на выходе
из канала вектор f будет правильно декодирован в переданный вектор
g тогда и только тогда, когда вектор ошибок e является образующим какого-либо смежного класса в таблице.
Таким образом, если смежный класс содержит вектор с весом, равным весу образующего, то такая таблица стандартного расположения не позволит правильно обнаружить все ошибки данного веса, и использование этого кода для передачи информации не оптимально.
Слайд 28Теорема о ТСР
Двоичным симметричным каналом называется канал, по которому передаются
символы 0 и 1 и для которого вероятность получения на
выходе 0 при посланном 0 равна вероятности получения на выходе 1 при посланной 1.
Теорема: Пусть G – линейный код, используемый для передачи информации по двоичному симметричному каналу. Пусть все кодовые векторы имеют одинаковую вероятность быть переданными. Тогда средняя вероятность правильного декодирования будет максимально возможной для данного кода, если в таблице стандартного расположения каждый образующий вектор имеет минимальный вес в своем смежном классе.
Слайд 29Последовательное декодирование
Весом смежного класса называется вес минимального по весу элемента
в этом смежном классе.
Пусть G – линейный (n,k,d)-код. Следующий алгоритм
называется последовательным декодированием.
Выписать в первую строку таблицы все вектора линейного подпространства G, начиная с нулевого.
Добавить к каждому кодовому вектору полученное на выходе из канала слово f и записать полученные вектора во вторую строку так, чтобы под вектором gi оказался вектор gi + f.
Слайд 30Последовательное декодирование
Вычислить вес полученного смежного класса G + f.
Если вес
класса равен 0, значит f – кодовое слово.
Если вес класса
не равен 0, следует найти в классе вектор минимального веса, выбрать в нем ненулевую координату и инвертировать эту координату во всех векторах класса.
В результате проведенной процедуры вес смежного класса уменьшится. Если вес стал равен 0, то образующий вектор полученного смежного класса и есть наиболее вероятное посланное слово. Иначе возвращаемся к шагу 5.
Слайд 31Синдром
Пусть G – линейный (n,k,d)-код, H – его проверочная матрица,
f – произвольный вектор пространства Vn. Тогда вектор s(f) =
f·HT называется синдромом вектора f.
Лемма 1: Два вектора f1 и f2 принадлежат одному и тому же смежному классу тогда и только тогда, когда их разность является кодовым словом.
Доказательство: Пусть f1, f2 G + h. Следовательно, f1 = g1 + h, f2 = g2 + h. Следовательно, f1 – f2 = g1 – g2 G, т.к. G – подпространство. Обратно: пусть f1 – f2 = g G. Следовательно, f1 = f2 + g. Пусть f1 G + h. Следовательно, f1 = g1 + h = f2 + g. Отсюда f2 = g – g1 + h = g2 + h G + h.
Слайд 32Синдром
Лемма 2: Два вектора f1 и f2 принадлежат одному и
тому же смежному классу тогда и только тогда, когда их
синдромы равны.
Доказательство: Пусть f1, f2 G + h. Следовательно, f1 – f2 = g G. Следовательно, (f1 – f2)·HT = 0. Следовательно, f1·HT – f2·HT = 0. Следовательно, f1·HT = f2·HT. То есть s(f1) = s(f2). В обратную сторону доказывается аналогично.
Слайд 33Таблица синдромов
Для декодирования с использованием синдромов следует создать таблицу синдромов.
Так
как в одном смежном классе все синдромы равны, а всего
смежных классов 2n – k, значит и различных синдромов будет 2n – k.
Матрица H имеет размер (n – k)n, следовательно матрица HT имеет размер n(n – k).
При вычислении синдрома следует вектор длины n умножить на матрицу размера n(n – k). В результате получается вектор длины n – k.
Слайд 34Таблица синдромов
Таким образом, в таблице синдромов должны содержаться все возможные
вектора длины n – k.
Мы знаем, что вектором ошибок для
принятого слова будет образующий смежного класса, которому принадлежит это слово. Причем декодирование будет оптимальным, если вес образующего минимально возможный.
Значит, для каждого синдрома следует найти вектор минимального веса, имеющий данный синдром. То есть вектор минимального веса, который будет ортогонален всем строкам проверочной матрицы H.
Слайд 35Таблица синдромов
В результате таблица синдромов состоит из двух столбцов. В
первом все возможные синдромы для данного кода, во втором –
образующие смежных классов, имеющие соответствующий синдром.
Таблица синдромов строится неоднозначно, если существуют несколько векторов одного минимального веса, подходящие на роль соответствующего образующего.
Слайд 36Декодирование с синдромами
Пусть G – линейный (n,k,d)-код. Следующий алгоритм позволяет
декодировать полученный вектор с помощью таблицы синдромов.
Вычислить синдром s(f) полученного
на выходе из канала слова f.
Найти этот синдром в таблице синдромов.
Вычесть из f образующий смежного класса, имеющий этот синдром. Полученное слово будет кодовым, а выбор образующего с минимальным весом при построении таблицы обеспечит наивысшую вероятность правильного декодирования.
Слайд 37Скорость передачи информации
Наряду с кодовым расстоянием d важным показателем оптимальности
кода является скорость передачи информации.
Пусть G – линейный (n,k,d)-код. Тогда
из каждых n переданных по каналу символов только k из них несут информацию. Значит, скорость передачи информации можно вычислить по формуле:
R = k/n.
Получается, что чем меньше проверочных символов, тем выше скорость. То есть хорошие корректирующие свойства кода и высокая скорость передачи информации – противоречивые требования.
Слайд 38Оптимальный выбор n,k,d
Среди кодов с фиксированными n и k лучшим
является код с наибольшим d.
Среди кодов с фиксированными n и
d лучшим является код с наибольшим k.
Среди кодов с фиксированными k и d лучшим является код с наименьшим n.
Рассмотрим некоторые границы, определяющие отношения между n, k и d.
Слайд 39Граница Синглтона
Теорема (граница Синглтона): Пусть G – линейный (n,k,d)-код. Тогда
k ≤ n – d + 1.
Линейные коды, для которых
k = n – d + 1 называются разделимыми кодами с максимальным расстоянием или МДР-кодами.
Слайд 40МДР-коды
МДР-коды имеют максимально возможное расстояние между кодовыми словами и могут
быть разделены на информационные и проверочные символы (то есть систематические
коды).
МДР-кодами являются коды с параметрами (n,1,n), (n,n–1,2) и (n,n,1).
Эти коды называются тривиальными МДР-кодами.
Других двоичных МДР-кодов не существует.
Слайд 41Верхняя граница Хемминга
Теорема (верхняя граница Хемминга): Пусть G – q-ичный
линейный (n,k,d)-код, исправляющий t ошибок (то есть t – целая
часть величины (d – 1)/2). Тогда
Коды, для которых граница Хемминга достигается (то есть выполняется равенство) называются совершенными или плотноупакованными кодами.
Слайд 42Совершенные коды
Тривиальными совершенными кодами являются коды с параметрами (n,1,n) при
нечетном n и (n,n,1).
Нетривиальными двоичными совершенными кодами являются коды Хемминга
и код Голея.
Код Хемминга порядка r имеет параметры (2r – 1, 2r – 1 – r, 3).
Код Голея имеет параметры (23,12,7).
Слайд 43Код Хемминга
Кодом Хемминга порядка r ≥ 2 называется двоичный код
с длиной блока n = 2r – 1, проверочная матрица
которого состоит из столбцов, представляющих собой двоичную запись номера столбца.
Код Хемминга порядка 2 имеет проверочную матрицу
Слайд 44Код Хемминга порядка 3
Код Хемминга порядка 3 имеет проверочную матрицу
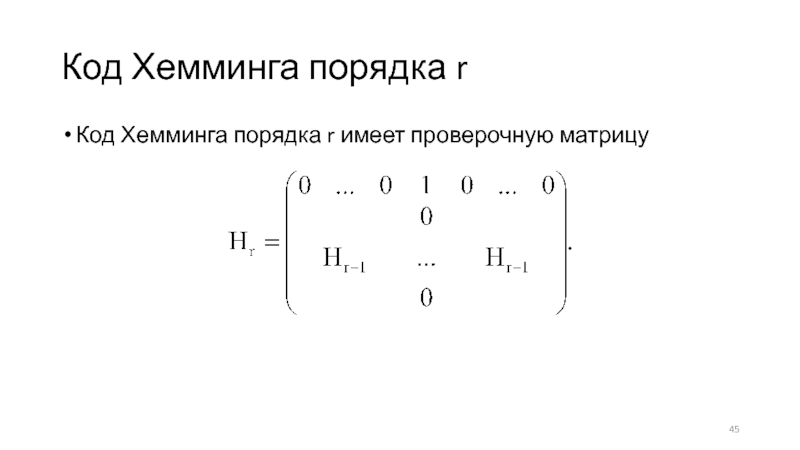
Слайд 45Код Хемминга порядка r
Код Хемминга порядка r имеет проверочную матрицу
Слайд 46Декодирование кода Хемминга
Код Хемминга имеет кодовое расстояние d = 3
и исправляет 1 ошибку.
Пусть принятое слово f = g +
e, где g – кодовое слово, а e – вектор ошибок веса 1.
При вычислении синдрома получим s(f) = f·HT = (g + e)·HT = g·HT + e·HT = 0 + e·HT = e·HT.
Но так как вектор e содержит только одну 1, то синдром s(f) будет равен транспонированному столбцу матрицы H, стоящему на том же месте, что и 1 в векторе e.
Слайд 47Декодирование кода Хемминга
Из построения кода Хемминга следует, что синдром равен
двоичной записи номера координаты, в которой произошла ошибка.
Таким образом, при
декодировании слова, переданного в коде Хемминга, следует вычислить его синдром, перевести полученную двоичную запись в десятичную систему и инвертировать координату с этим номером.
Слайд 48Верхняя граница Плоткина
Теорема (верхняя граница Плоткина): Пусть G – q-ичный
линейный (n,k,d)-код мощности M. Тогда
Коды, для которых граница Плоткина достигается
(то есть выполняется равенство), называются эквидистантными.
Слайд 49Эквидистантные коды
Для эквидистантного кода расстояние между двумя любыми кодовыми словами
одинаково.
Тривиальным эквидистантным кодом является код кратных повторений.
Эквидистантными кодами являются коды
с параметрами (2,3,2) – симплексные коды порядка r.
Слайд 50Нижняя граница Варшамова-Гильберта
Теорема (нижняя граница Варшамова-Гильберта): Существует q-ичный линейный (n,k,d)-код,
удовлетворяющий неравенству
Слайд 51Двойственный код
Пусть G – линейный (n,k,d)-код с проверочной матрицей H.
Тогда код, для которого матрица H будет порождающей, называется двойственным
к коду G.
Таким образом, линейный код, двойственный к коду G, является линейным пространством, ортогональным к линейному пространству G.
Очевидно, что порождающая матрица кода G станет проверочной матрицей для двойственного к G кода.
Слайд 52Симплексный код
Код, двойственный к коду Хемминга, называется симплексным кодом.
Проверочная матрица
кода Хемминга является порождающей для симплексного кода.
Симплексный код порядка r
имеет параметры (2r – 1, r, 2r–1).
Симплексный код является эквидистантным – расстояние между любыми двумя словами кода равно 2r–1.
Симплексный код порядка r обозначается Σr.
Если рассматривать кодовые слова этого кода как векторы, то они образуют n-мерный тетраэдр (симплекс).
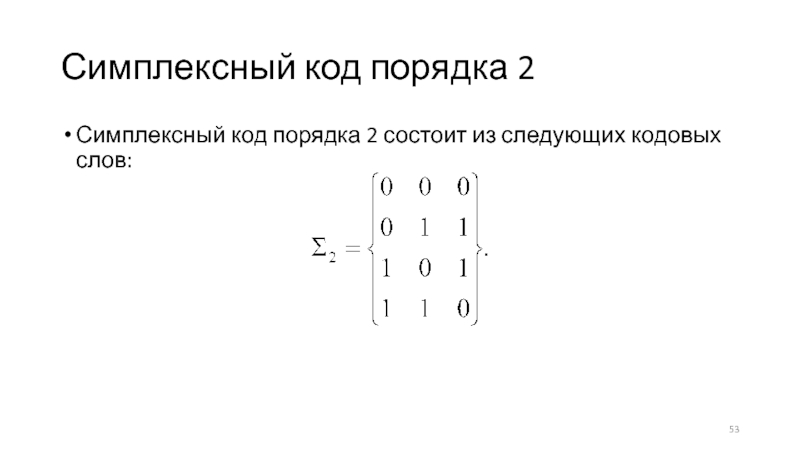
Слайд 53Симплексный код порядка 2
Симплексный код порядка 2 состоит из следующих
кодовых слов:
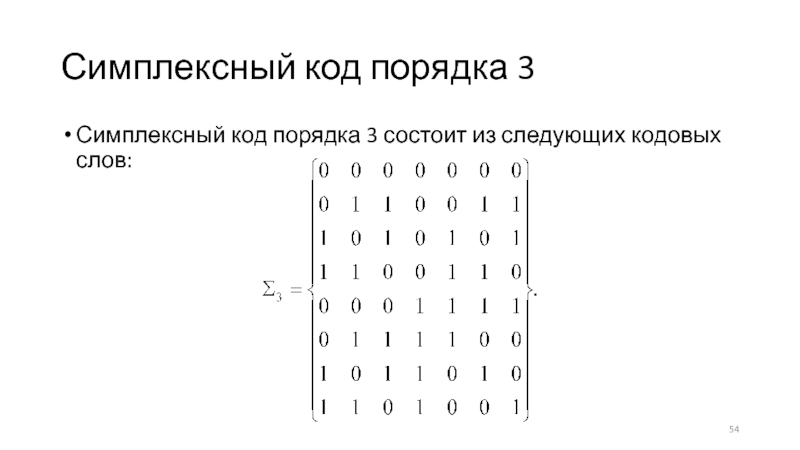
Слайд 54Симплексный код порядка 3
Симплексный код порядка 3 состоит из следующих
кодовых слов:
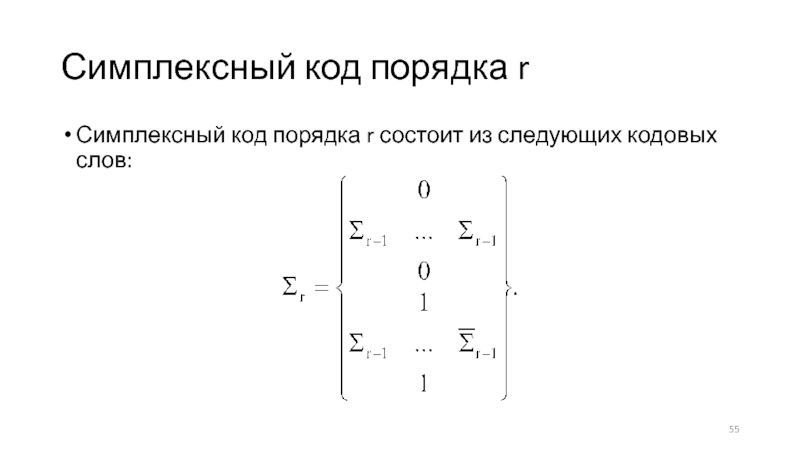
Слайд 55Симплексный код порядка r
Симплексный код порядка r состоит из следующих
кодовых слов:
Слайд 56Добавление общей проверки на четность
Пусть G – двоичный линейный (n,k,d)-код,
в котором есть слова нечетного веса. Новый код G’ можно
получить из кода G добавлением (n + 1)-й координаты, равной сумме предыдущих n координат.
В этом случае n’ = n + 1, k’ = k, d’ = d + 1 при нечётном d и d’ = d при чётном d.
Слайд 57Выкалывание кодовых координат
Пусть G – двоичный линейный (n,k,d)-код. Новый код
G’ можно получить из кода G удалением из всех слов
любой кодовой координаты.
В этом случае n’ = n – 1, k’ = k или k – 1, d’ = d или d – 1.
Слайд 58Выбрасывание слов
Пусть G – двоичный линейный (n,k,d)-код. Новый код G’
можно получить из кода G удалением всех кодовых слов нечётного
веса.
В этом случае n’ = n, k’ = k – 1, d’ ≥ d.
Слайд 59Добавление слов
Пусть G – двоичный линейный (n,k,d)-код, и вектор f
= (1…1) не лежит в коде G. Новый код G’
можно получить из кода G добавлением новых кодовых слов множества G + f.
В этом случае n’ = n, k’ = k + 1, d’ = min {d, n – max w(g)}.
Если после этого добавить общую проверку на чётность, то можно получить параметры n’ = n + 1, k’ = k + 1. То есть произошло добавление нового информационного символа.
Слайд 60Укорочение кода
Пусть G – двоичный линейный (n,k,d)-код. Новый код G’
можно получить, выбрав из кода G все вектора с первой
нулевой координатой и удалив эту координату.
В этом случае n’ = n – 1, k’ = k – 1, d’ ≥ d.
Слайд 61Прямая сумма
Пусть G1 – двоичный линейный (n1,k1,d1)-код, G2 – двоичный
линейный (n2,k2,d2)-код. Новый код G можно получить, дописав к каждому
слову кода G1 всевозможные варианты слов из кода G2.
Таким образом, слово из G будет иметь вид uv, где u G1, v G2.
В этом случае n = n1 + n2, k = k1 + k2, d = min {d1, d2}.
Слайд 62Полупрямая сумма
Пусть G1 – двоичный линейный (n1,k1,d1)-код, G2 – двоичный
линейный (n1,k2,d2)-код. Новый код G можно получить, дописав к каждому
слову кода G1 всевозможные варианты сумм этого слова из кода G1 и слов из кода G2.
Таким образом, слово из G будет иметь вид u(u+v), где u G1, v G2.
В этом случае n = 2n1, k = k1 + k2, d = min {2d1, d2}.
Слайд 63Произведение кодов
Пусть G1 – двоичный линейный систематический (n1,k1,d1)-код, G2 –
двоичный линейный систематический (n2,k2,d2)-код. Запишем k = k1·k2 всевозможных
информационных символов в виде матрицы размера k2k1. Строки матрицы закодируем кодом G1, дописав в каждую строку соответствующие (n1 – k1) проверочных символов. Столбцы матрицы закодируем кодом G2, дописав в каждый столбец соответствующие (n2 – k2) проверочных символов. Выписывая по строчкам кодовые символы из матрицы, получим новое кодовое слово. Полученный таким образом код G = G1G2 называется произведением кодов G1 и G2.
В этом случае n = n1n2, k = k1k2, d ≥ d1d2.
Слайд 64Спектр кода
Весовым спектром линейного (n,k,d)-кода G называется вектор A =
(A0, A1, …, An), где Ai = |{g G|w(g)
= i}|.