Алгоритмические основы трехмерной графики

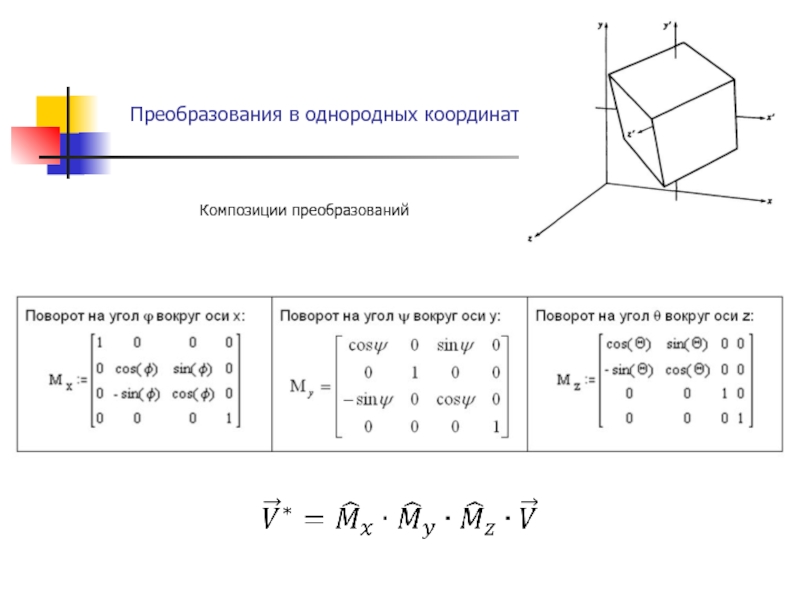
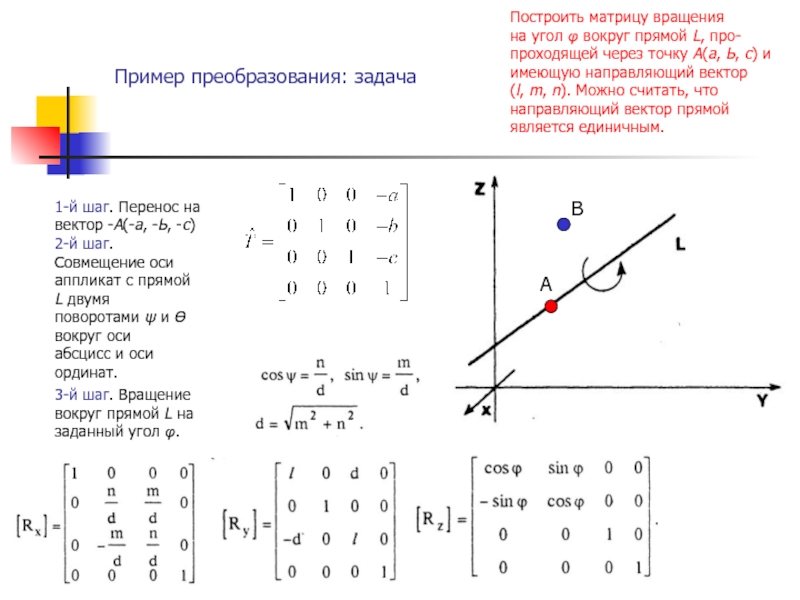
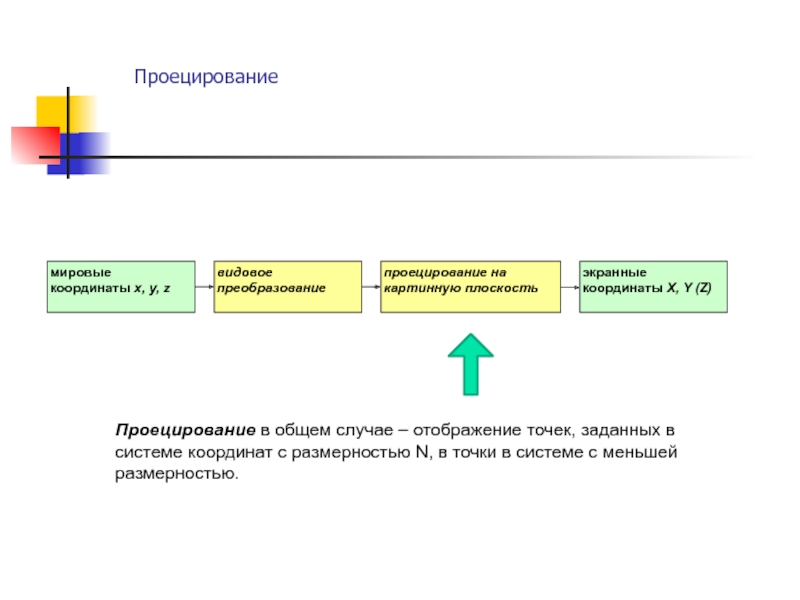
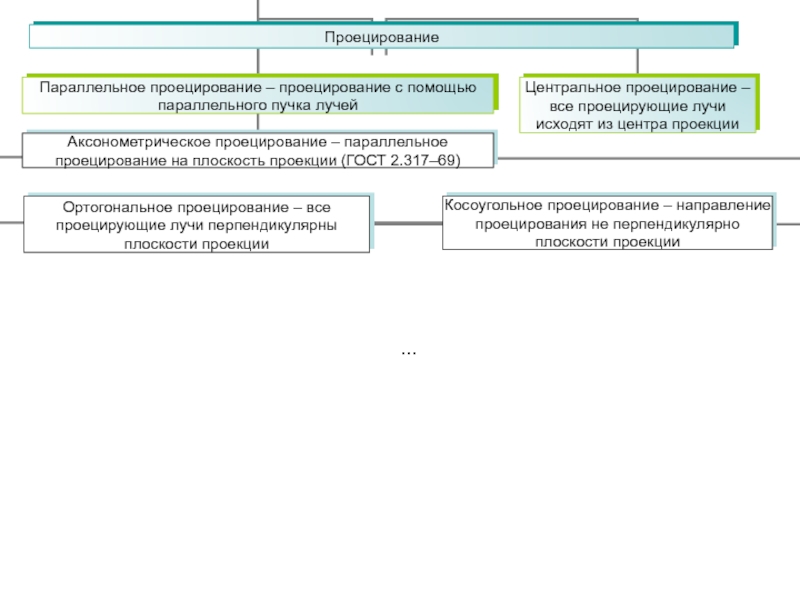
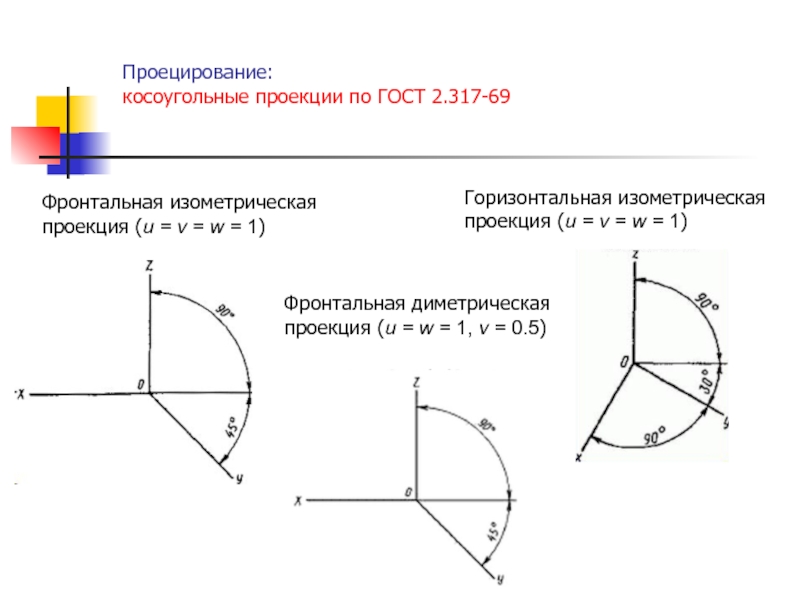
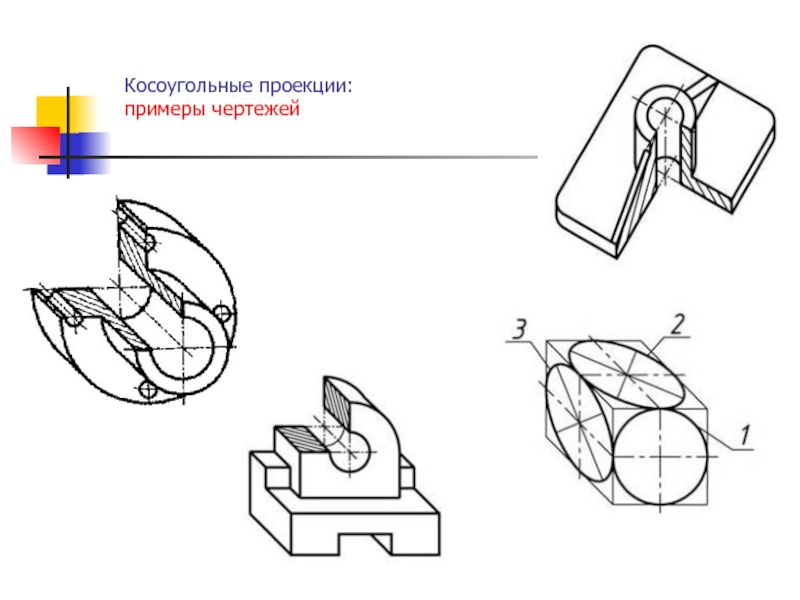
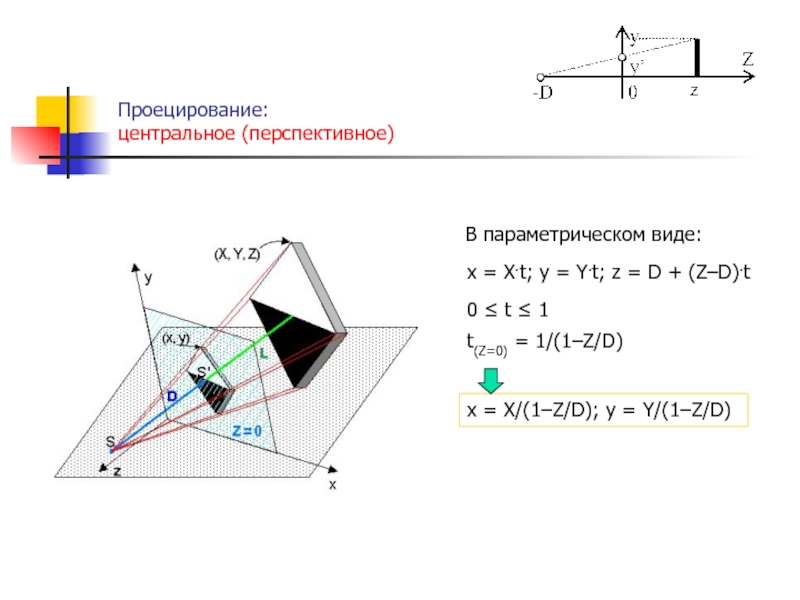
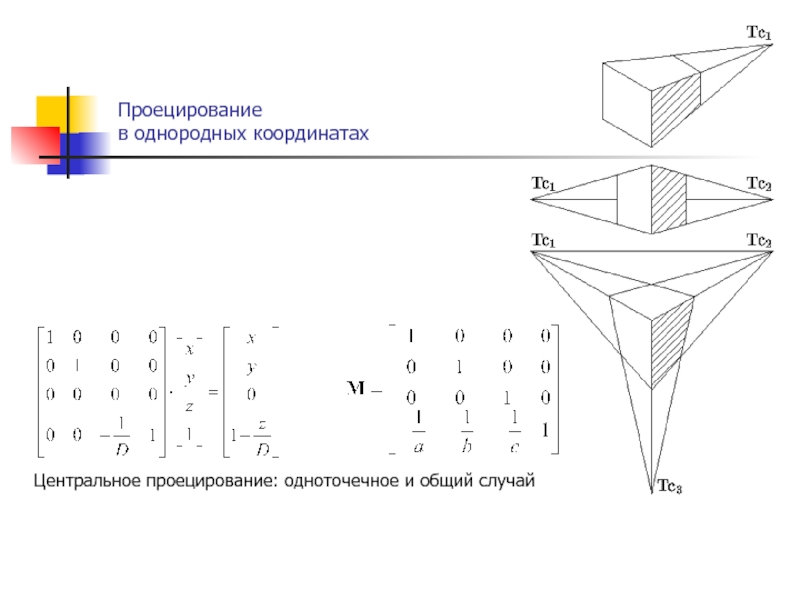
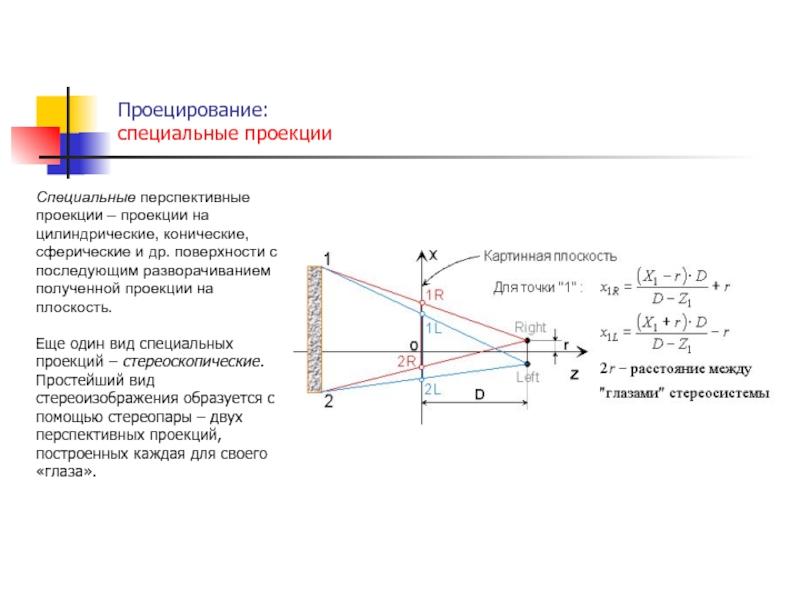
функции fi – линейные относительно аргументов (k1, k2, …, kn),

то такие преобразования называют линейными, а при n = N – аффинными

Преобразования координат в явном и неявном виде широко используются в компьютерной графике с целью описания графического объекта в наиболее удобных координатных системах, для изменения масштаба элементов чертежа, построения проекций пространственных образов, направленной деформации объектов.

1 ] = [ (x/w) (y/w) (z/w) 1 ]
Использование

механизма однородных координат позволяет применять единый математический аппарат для пространственных преобразований (поворотов, масштабирования, переноса) точек, прямых, квадратичных и бикубических поверхностей и линий

выполняя три поворота вокруг двух координатных осей, при этом для

первого (ψ) и третьего (φ) поворота берется одна ось, которая в процессе преобразования сама поворачивается (θ).

матрицу вращения
на угол φ вокруг прямой L, про-
проходящей

через точку А(а, Ь, с) и
имеющую направляющий вектор
(l, m, n). Можно считать, что
направляющий вектор прямой
является единичным.

2-й шаг. Совмещение оси аппликат с прямой L двумя поворотами ψ и Ө
вокруг оси абсцисс и оси ординат.

3-й шаг. Вращение вокруг прямой L на заданный угол φ.

A

B

-Ө.
5-й шаг. Поворот вокруг оси абсцисс на угол -ψ.
6-й

шаг. Перенос на вектор А(а, Ь, с).

Окончательно:

координат с размерностью N, в точки в системе с меньшей

размерностью.

рядом общих свойств:

Проекция точки есть точка. При заданном центре Р

(или направлении S) проецированию любой точки А пространства соответствует на плоскости проекций p' единственная точка А'.

Проекция прямой есть прямая.

2.1) При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций: АВ/ВС = А'В'/В'С.
2.2) При параллельном проецировании проекции параллельных прямых есть прямые параллельные.

проекций, то проекции ее плоских фигур при центральном проецировании подобны

самим фигурам, а при параллельном — равны им.

При параллельном проецировании проекция фигуры не изменяется при параллельном переносе плоскости проекций.

них принято располагать горизонтально (горизонтальная плоскость проекций), другую – вертикально

(фронтальная плоскость проекций). Иногда используется третья плоскость – перпендикулярная двум первым (профильная плоскость проекций).

Ортогональное (прямоугольное) проецирование есть частный случай проецирования параллельного, когда все проецирующие лучи перпендикулярны плоскости проекций.

направление проецирования не перпендикулярно плоскости аксонометрических проекций;

2) прямоугольные, когда направление

проецирования перпендикулярно плоскости аксонометрических проекций.

В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:

1) изометрия: u = v = w
2) диметрия: u ≠ v = w или u = v ≠ w
3) триметрия: u ≠ v ≠ w

φ — угол между направлением проецирования и плоскостью аксонометрических проекций. В случае φ = 90° u2 + v2 + w2 = 2.

и бесконечное множество диметрических и триметрических проекций.
Прямоугольная изометрия

Зu2 =

2,

u = (2/3)1/2 и u = v = w = 0,82.

ГОСТ 2.317—69 : u = v = w = 1.

2,
u = w = (8/9)1/2 = 0.94
v = 0.47.

ГОСТ 2.317—69 : u = w = 1, v=0.5.

– когда угол наклона проектирующих лучей к плоскости экрана равен

половине прямого, и кабинетную – частный случай свободной проекции, при котором масштаб по третьей оси вдвое меньше.

= w = 1)

Горизонтальная изометрическая проекция (u = v =

w = 1)

Фронтальная диметрическая проекция (u = w = 1, v = 0.5)

аксонометрической проекции.
Для изометрии ϕ = 35°; ψ = -45°
Для диметрии

ϕ = 20°; ψ = -20°

- фронтальная изометрическая

- фронтальная диметрическая

+ (Z–D).t
0 ≤ t ≤ 1
t(Z=0) = 1/(1–Z/D)

В параметрическом виде:

x = X/(1–Z/D); y = Y/(1–Z/D)

и др. поверхности с последующим разворачиванием полученной проекции на плоскость.

Еще один вид специальных проекций – стереоскопические. Простейший вид стереоизображения образуется с помощью стереопары – двух перспективных проекций, построенных каждая для своего «глаза».