Арифметическая и геометрическая прогрессии

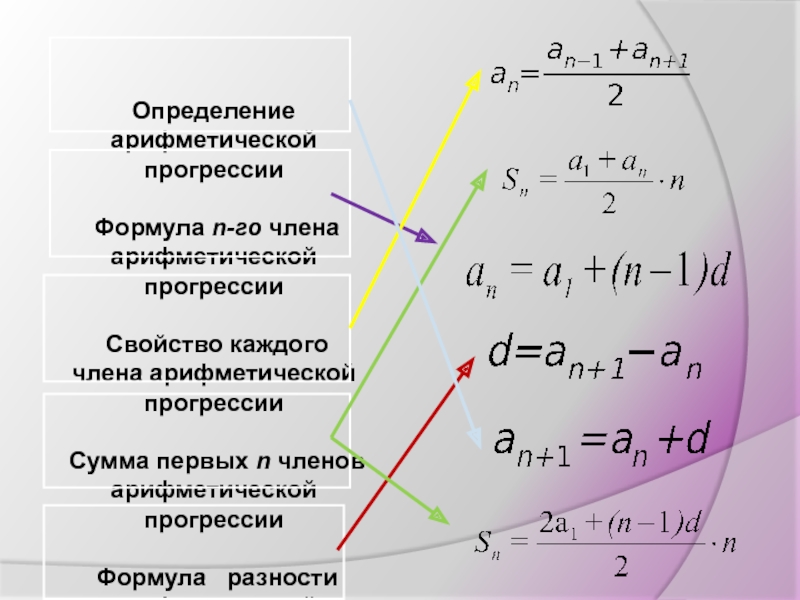
равен предыдущему, сложенному с одним и тем же числом.
Последовательность отличных

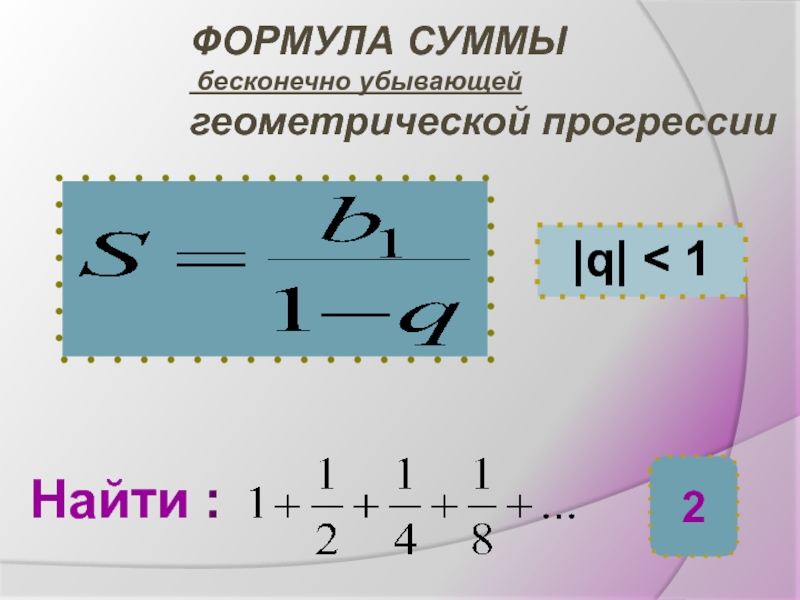
от нуля чисел в которой каждый член начиная со второго равен предыдущему умноженному на одно и тоже число.

Число d - разность прогрессии

Число q - знаменатель прогрессии.

d = a2-a1 = a3-a2 = a4-a3 =….

q = b2:b1 = b3:b2 = b4:b3 =…

5
Найти: a4,.
a4=22
bn=b1qn-1
Дано: b1 = 3, q = 2
Найти: b3.
b3=12

арифметической,

геометрической

среднее арифметическое между предыдущим и последующим членами прогрессии
Каждый член последовательности

начиная со второго есть среднее геометрическое между предыдущим и последующим членами последовательности (bn >0)

Характеристическое свойство прогрессий

х1, х2, 4, х4,14, … найти: х4

b1, b2, 1, b4, 16, …- все члены положительные числа найти: b4

Х4=9

b4=4

4
Найти: S5
S5 = 65
Дано: b 1 = 2, q =

- 3

Найти: S4

S4 = - 40

арифметическая

геометрическая

а7 = 8, а8 = 12. найдите разность арифметической прогрессии.
А)

-4

Б) 4

В) 20

Г) 3

Б) 18

В) 3

Г) 9

3. Члены арифметической чисел является членом этой прогрессии?

3. Найдите сумму семи первых членов геометрической прогрессии 4; 8; …

А) - 254

Б) 508

В) 608

Г) - 508

Часть I ( 0,5 балла )

А) -3

3. Члены арифметической прогрессии изображены (рис.1) точками на коорди- натной плоскости. Какое из данных ч

2 балла)
5. В геометрической прогрессии (bn) b1 = 8, b3

= 24. Найдите b5. ( для q > 0 )

(задания на 3 балла)

6. Сумма второго и пятого членов арифметической прогрессии равна 11. Третий её член на 6 больше первого. Найдите второй и четвёртый члены.

Критерии оценок:

b5 = 72

Ответ:

Ответ:

а2 =1; а4 = 7,

на 20 мест больше чем в предыдущем, а в последнем

ряду 280 мест. Сколько человек вмещает амфитеатр?

В сборнике по подготовке к экзамену-240 задач. Ученик планирует начать их решение 2 мая, а закончить 16 мая, решая каждый день на две задачи больше, чем в предыдущий день. Сколько задач ученик запланировал решить 12 мая?

Прогрессии в жизни, в быту

проверкой )
VI (слайд 13 ) решение практических задач

- Решение:
280= а1 + 20∙(10-1);
а1= 280 - 20 ∙ 9 = 100;
S10 = ½(100+280) ∙ 10 =1900.
Ответ:1900 человек вмещает амфитеатр.

- Решение: 240=½(2 а1 +2 ∙14) ∙ 15;
240:15= а₁ + 14; а₁ = 2;
а₁₁ = 2+2 ∙ 10 = 22.
Ответ:22 задачи надо решить 12 мая.

арифметической прогрессии Формула n-го члена арифметической прогрессии Свойство каждого члена арифметической прогрессии Сумма первых n членов арифметической прогрессии Формула разности арифметической прогрессии