Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
БАЗЫ ДАННЫХ
Содержание
- 1. БАЗЫ ДАННЫХ
- 2. Реляционная модель данных. Реляционная алгебра
- 3. Реляционная алгебра представляет собой набор операторов, использующих
- 4. Реляционная модель данных. Реляционная алгебра
- 5. Графическая интерпретация некоторых операций реляционной алгебры
- 6. Реляционная модель данных. Реляционная алгебра
- 7. Реляционная модель данных. Реляционная алгебра
- 8. Слайд 8
- 9. Реляционная модель данных. Реляционная алгебра
- 10. Слайд 10
- 11. Реляционная модель данных. Реляционная алгебра
- 12. Слайд 12
- 13. Реляционная модель данных. Реляционная алгебра
- 14. Пример 4 Пусть даны два отношения и с информацией о поставщиках и деталях
- 15. Декартово произведение отношений Aи B Отношение A
- 16. Реляционная модель данных. Реляционная алгебра
- 17. Пример 5 Пусть дано отношение с
- 18. Реляционная модель данных. Реляционная алгебра
- 19. Слайд 19
- 20. Реляционная модель данных. Реляционная алгебра
- 21. Реляционная модель данных. Реляционная алгебра
- 22. Слайд 22
- 23. Ответ на вопрос, какие детали поставляются
- 24. Недостатком эквисоединения является то, что если
- 25. Реляционная модель данных. Реляционная алгебра
- 26. Реляционная модель данных. Реляционная алгебра
- 27. Слайд 27
- 28. Реляционная модель данных. Реляционная алгебра
- 29. Пример 9 В примере с
- 30. Реляционная модель данных. Реляционная алгебра
- 31. Реляционная модель данных. Реляционная алгебра.
- 32. Реляционная модель данных. Реляционная алгебра
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Скачать презентанцию
Реляционная модель данных. Реляционная алгебра Вторая часть реляционной модели, манипуляционная часть, утверждает, что доступ к реляционным данным осуществляется при помощи реляционной алгебры или эквивалентного ему реляционного исчисления. В реализациях
Слайды и текст этой презентации
Слайд 1Лебедева Т.Ф.
2014г.
БАЗЫ ДАННЫХ
Кемеровский институт (филиал) РЭУ им. Г.В. Плеханова
Экономический факультет
Слайд 2Реляционная модель данных.
Реляционная алгебра
Вторая часть реляционной модели, манипуляционная
часть, утверждает, что доступ к реляционным данным осуществляется при помощи
реляционной алгебры или эквивалентного ему реляционного исчисления.В реализациях конкретных реляционных СУБД сейчас не используется в чистом виде ни реляционная алгебра, ни реляционное исчисление.
Фактическим стандартом доступа к реляционным данным стал язык SQL (Structured Query Language). Язык SQL представляет собой смесь операторов реляционной алгебры и выражений реляционного исчисления, использующий синтаксис, близкий к фразам английского языка и расширенный дополнительными возможностями, отсутствующими в реляционной алгебре и реляционном исчислении.
Вообще, язык доступа к данным называется реляционно полным, если он по выразительной силе не уступает реляционной алгебре (или, что то же самое, реляционному исчислению), т.е. любой оператор реляционной алгебры может быть выражен средствами этого языка. Именно таким и является язык SQL.
Слайд 3
Реляционная алгебра представляет собой набор операторов, использующих отношения в качестве
аргументов, и возвращающие отношения в качестве результата. Таким образом, реляционный
оператор выглядит как функция с отношениями в качестве аргументов:Реляционная алгебра является замкнутой, т.к. в качестве аргументов в реляционные операторы можно подставлять другие реляционные операторы, подходящие по типу.
Каждое отношение обязано иметь уникальное имя в пределах базы данных. Имя отношения, полученного в результате выполнения реляционной операции, определяется в левой части равенства. Однако можно не требовать наличия имен от отношений, полученных в результате реляционных выражений, если эти отношения подставляются в качестве аргументов в другие реляционные выражения. Такие отношения будем называть неименованными отношениями. Неименованные отношения реально не существуют в базе данных, а только вычисляются в момент определения значения реляционного оператора.
Реляционная модель данных.
Реляционная алгебра
Слайд 4Реляционная модель данных.
Реляционная алгебра
Традиционно, вслед за Э. Коддом,
определяют восемь реляционных операций реляционной алгебры, объединенных в две группы.
1 Теоретико-множественные операции:
объединение;
пересечение;
вычитание;
декартово произведение.
2 Специальные реляционные операции:
выборка (селекция, ограничение) ;
проекция;
соединение;
деление.
Слайд 6Реляционная модель данных.
Реляционная алгебра
Не все они являются независимыми,
т.е. некоторые из этих операций могут быть выражены через другие
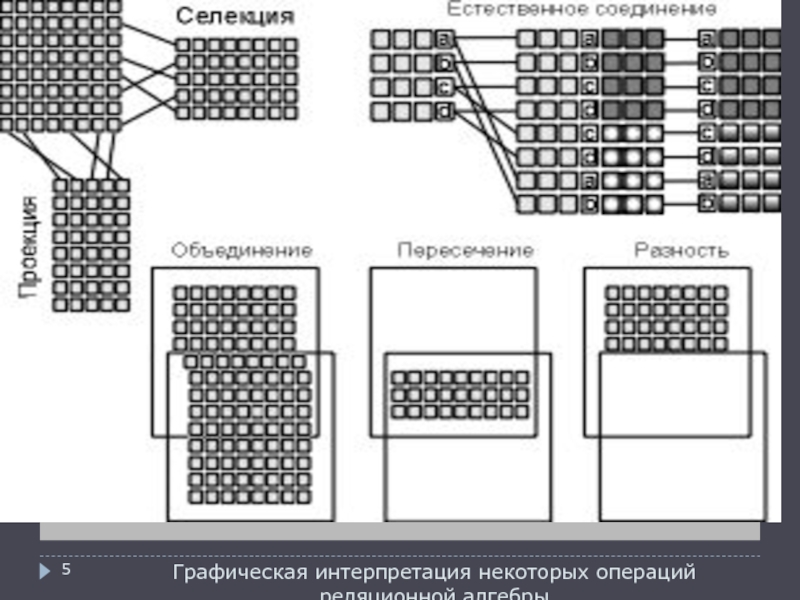
реляционные операции. Каждая операция реляционной алгебры использует одну или несколько таблиц (отношений) в качестве своих операндов и продуцирует в результате новую таблицу, т.е. позволяет «разрезать» или «склеивать» таблицы (рис.)Кроме того, в состав алгебры включается операция присваивания, позволяющая сохранить в базе данных результаты вычисления алгебраических выражений, и
операция переименования атрибутов, дающая возможность корректно сформировать заголовок (схему) результирующего отношения. Если не вдаваться в некоторые тонкости, которые мы рассмотрим в следующих подразделах, то почти все операции предложенного выше набора обладают очевидной и простой интерпретацией:
Слайд 7Реляционная модель данных.
Реляционная алгебра
Объединение. При выполнении операции объединения
двух отношений производится отношение, включающее все кортежи, входящие хотя бы
в одно из отношений-операндов.Объединением двух совместимых по типу отношений A и B называется отношение с тем же заголовком, что и у отношений A и B , и телом, состоящим из кортежей, принадлежащих или A , или B, или обоим отношениям.
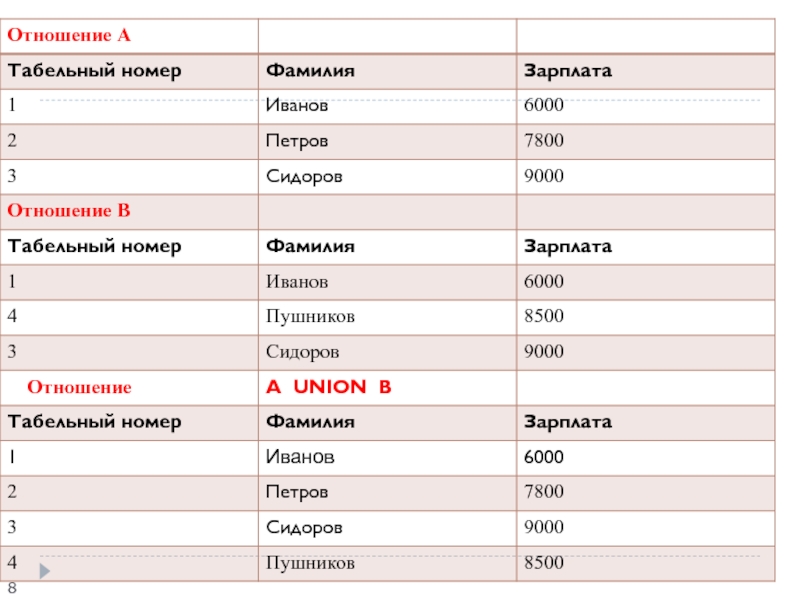
Синтаксис операции объединения: A UNION B
Объединение, как и любое отношение, не может содержать одинаковых кортежей. Поэтому, если некоторый кортеж входит и в отношение A, и отношение B , то в объединение он входит один раз.
Пример 1 Пусть даны два отношения и с информацией о сотрудниках:
Слайд 9Реляционная модель данных.
Реляционная алгебра
2. Пересечение. Операция пересечения двух
отношений производит отношение, включающее все кортежи, входящие в оба отношения-операнда.
Пересечением двух совместимых по типу отношений A и B называется отношение с тем же заголовком, что и у отношений А и В , и телом, состоящим из кортежей, принадлежащих одновременно обоим отношениям А и В .
Синтаксис операции пересечения: A INTERSECT B
Пример 2 Для тех же отношений А и В , что и в предыдущем примере пересечение
Слайд 11Реляционная модель данных.
Реляционная алгебра
3. Разность. Отношение, являющееся разностью
двух отношений включает все кортежи, входящие в отношение - первый
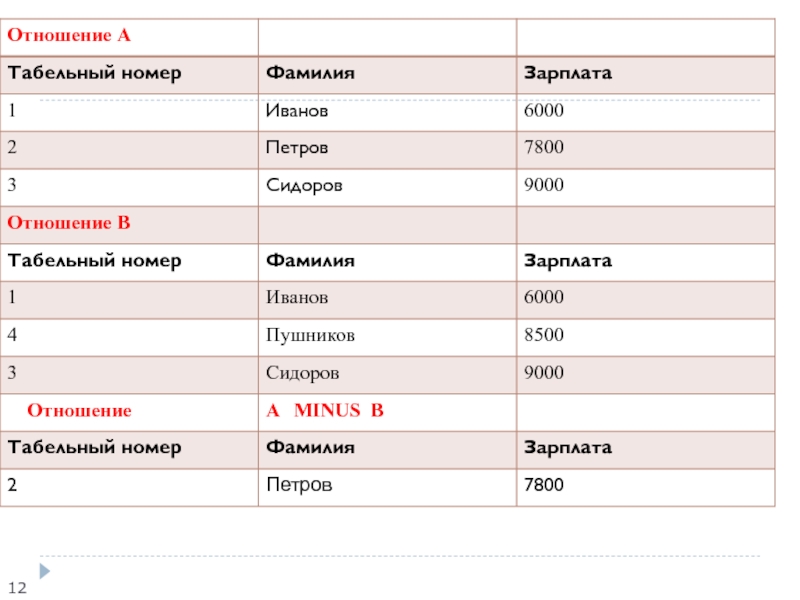
операнд, такие, что ни один из них не входит в отношение, являющееся вторым операндом. Вычитанием (разностью) двух совместимых по типу отношений и называется отношение с тем же заголовком, что и у отношений А и В , и телом, состоящим из кортежей, принадлежащих отношению А и не принадлежащих отношению В .Синтаксис операции вычитания: A MINUS B
Пример 3 Для тех же отношений и , что и в предыдущем примере вычитание Отношение A MINUS B имеет вид:
Слайд 13Реляционная модель данных.
Реляционная алгебра
4. Декартово произведение. При выполнении
прямого произведения двух отношений производится отношение, кортежи которого являются конкатенацией
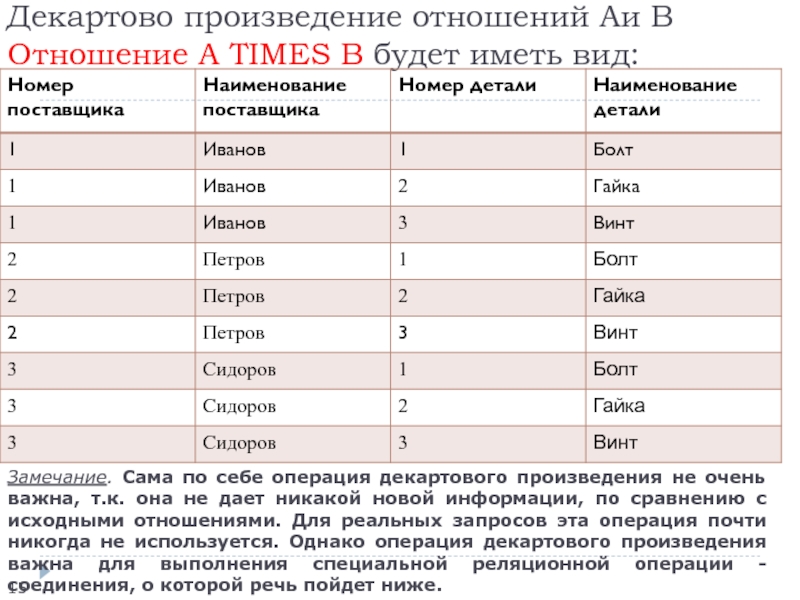
(сцеплением) кортежей первого и второго операндов. Декартовым произведением двух отношений и называется отношение, заголовок которого является сцеплением заголовков отношений A(a1,a2,...an) и B(b1,b2,b3,…bm) , а тело состоит из кортежей, являющихся сцеплением кортежей отношений A и B .Синтаксис операции декартового произведения: A TIMES B
Замечание 1. Мощность произведения равна произведению мощностей отношений A и B , (n*m) т.к. каждый кортеж отношения А соединяется с каждым кортежем отношения В.
Замечание 2. Если в отношения A и B имеются атрибуты с одинаковыми наименованиями, то перед выполнением операции декартового произведения такие атрибуты необходимо переименовать.
Замечание 3. Перемножать можно любые два отношения, совместимость по типу при этом не требуется.
Слайд 15Декартово произведение отношений Aи B Отношение A TIMES B будет
иметь вид:
Замечание. Сама по себе операция декартового произведения не
очень важна, т.к. она не дает никакой новой информации, по сравнению с исходными отношениями. Для реальных запросов эта операция почти никогда не используется. Однако операция декартового произведения важна для выполнения специальной реляционной операции - соединения, о которой речь пойдет ниже.Слайд 16Реляционная модель данных.
Реляционная алгебра
5. Ограничение (выборка, селекция). Результатом
ограничения отношения А по некоторому условию С является отношение, включающее
кортежи отношения-операнда, удовлетворяющее этому условию.Выборкой (ограничением, селекцией) на отношении A с условием C называется отношение с тем же заголовком, что и у отношения A , и телом, состоящем из кортежей, значения атрибутов которых при подстановке в условие C дают значение ИСТИНА.
C представляет собой логическое выражение, в которое могут входить атрибуты отношения и (или) скалярные выражения.
В простейшем случае условие C имеет вид XѲY, где Ѳ - один из операторов сравнения ( =, >,<, ≤, ≥ ≠ и т.д.), а X и Y - атрибуты отношения или скалярные значения.
Синтаксис операции выборки: A where C , или A where XѲY
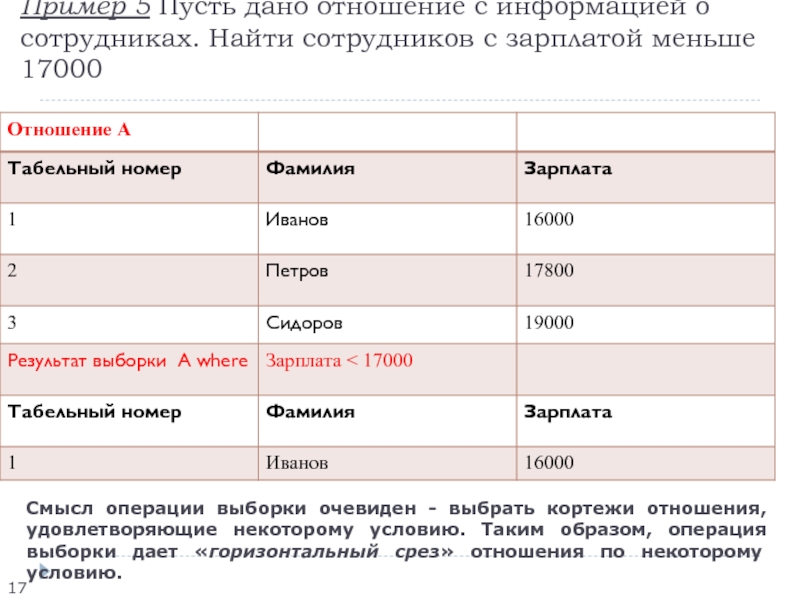
Слайд 17 Пример 5 Пусть дано отношение с информацией о сотрудниках. Найти
сотрудников с зарплатой меньше 17000
Смысл операции выборки очевиден -
выбрать кортежи отношения, удовлетворяющие некоторому условию. Таким образом, операция выборки дает «горизонтальный срез» отношения по некоторому условию. Слайд 18Реляционная модель данных.
Реляционная алгебра
6. Проекция. При выполнении проекции
отношения на заданный набор его атрибутов производится отношение, кортежи которого
производятся путем взятия соответствующих значений из кортежей отношения-операнда.Проекцией отношения A по атрибутам X,Y,…Z , где каждый из атрибутов принадлежит отношению A, называется отношение с заголовком (X,Y,…Z) и телом, содержащим множество кортежей вида (x,y,…z) , таких, для которых в отношении A найдутся кортежи со значением атрибута X, равным x, значением атрибутаY, равным y , …, значением атрибута Z, равным z.
Синтаксис операции проекции: A[X,Y,…Z]
Замечание. Операция проекции дает «вертикальный срез» отношения, в котором удалены все возникшие при таком срезе дубликаты кортежей.
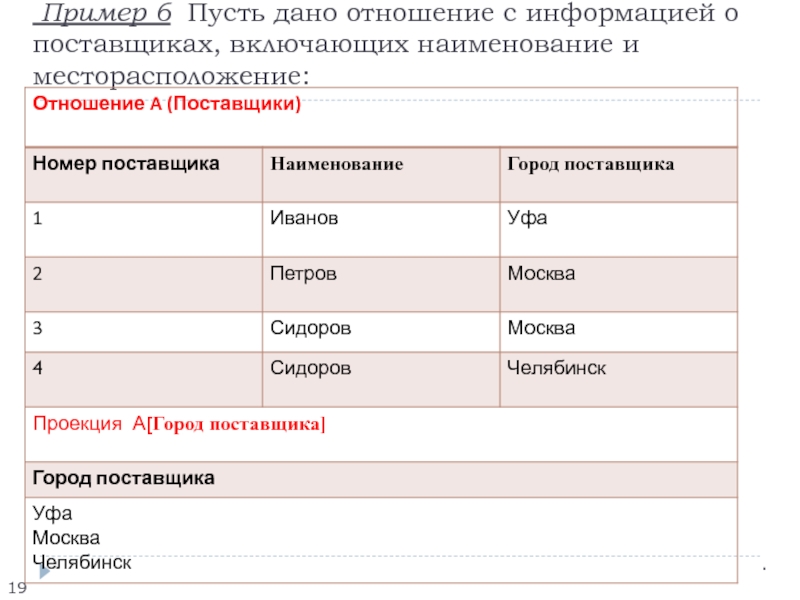
Слайд 19 Пример 6 Пусть дано отношение с информацией о поставщиках,
включающих наименование и месторасположение:
.
Слайд 20Реляционная модель данных.
Реляционная алгебра
7. Соединение. При соединении
двух отношений по некоторому условию образуется результирующее отношение, кортежи которого
являются сцеплением кортежей первого и второго отношений и удовлетворяют этому условию.Соединением отношений A и B по условию C называется отношение
( A TIMES B) where C
C представляет собой логическое выражение, в которое могут входить атрибуты отношений A и B и (или) скалярные выражения. Таким образом, операция соединения есть результат последовательного применения операций декартового произведения и выборки. Если в отношениях A и B имеются атрибуты с одинаковыми наименованиями, то перед выполнением соединения такие атрибуты необходимо переименовать.
Операция соединения отношений, наряду с операциями выборки и проекции, является одной из наиболее важных реляционных операций.
Слайд 21Реляционная модель данных.
Реляционная алгебра
Обычно рассматривается несколько разновидностей операции
соединения:
общая операция соединения;
Ѳ -соединение (тэта-соединение);
эквисоединение;
естественное соединение
Наиболее важным из этих частных случаев является операция естественного соединения. Все разновидности соединения являются частными случаями общей операции соединения.
Тэта-соединение. Пусть отношение A содержит атрибут X, отношение B
содержит атрибут Y , а Ѳ - один из операторов сравнения ( =, >,<, ≤, ≥ ≠ и т.д.). Тогда Ѳ -соединением отношения A по атрибуту X с отношением B по атрибуту Y называют отношение ( A TIMES B) where X Ѳ Y
Это частный случай операции общего соединения.
Эквисоединение. Наиболее важным частным случаем Ѳ -соединения является случай, когда Ѳ есть просто равенство. Синтаксис эквисоединения:
A [X=Y] B
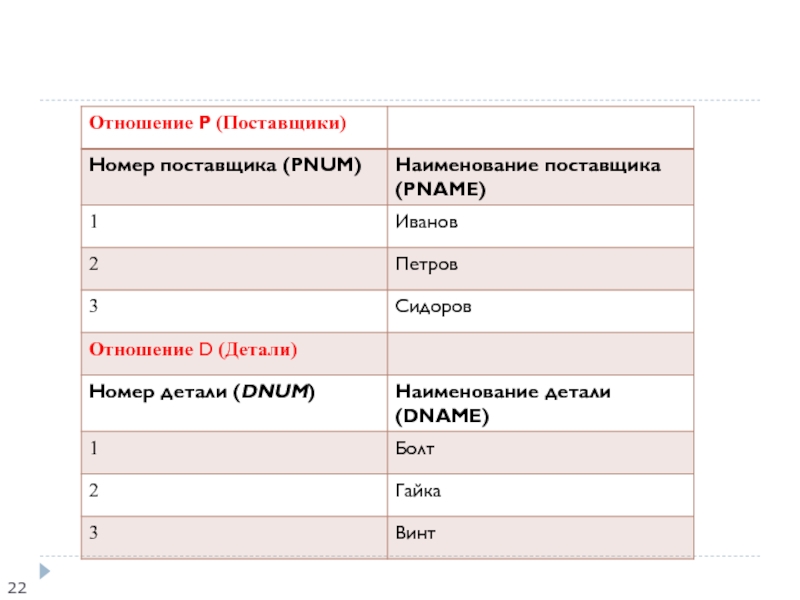
Пример 7 Пусть имеются отношения P, D и PD , хранящие информацию о поставщиках, деталях и поставках соответственно (для удобства введем краткие наименования атрибутов):
Слайд 23
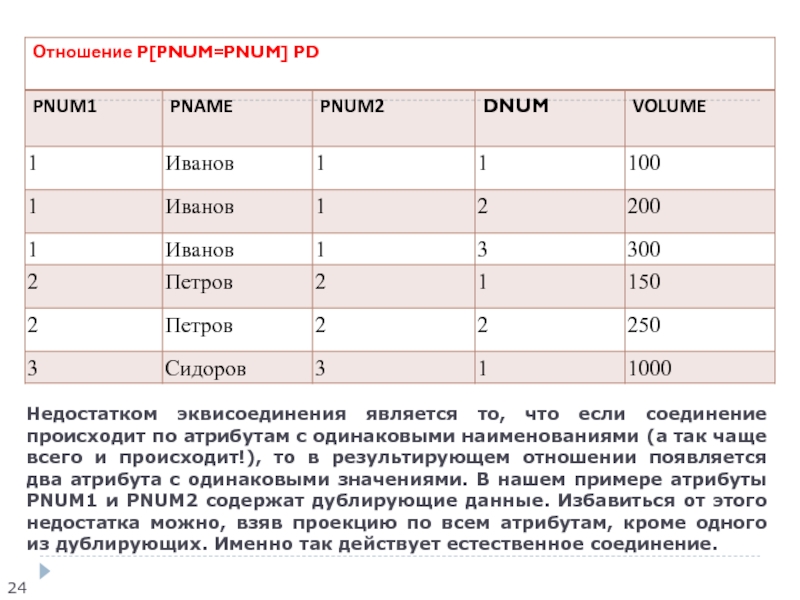
Ответ на вопрос, какие детали поставляются поставщиками, дает эквисоединение P[PNUM=PNUM]
PD. На самом деле, т.к. в отношениях P, PD имеются
одинаковые атрибуты, то требуется сначала переименовать атрибуты, а потом выполнить эквисоединение. В результате имеем отношение, отвечающее на вопрос «Какие детали поставляются какими поставщиками?»Слайд 24
Недостатком эквисоединения является то, что если соединение происходит по атрибутам
с одинаковыми наименованиями (а так чаще всего и происходит!), то
в результирующем отношении появляется два атрибута с одинаковыми значениями. В нашем примере атрибуты PNUM1 и PNUM2 содержат дублирующие данные. Избавиться от этого недостатка можно, взяв проекцию по всем атрибутам, кроме одного из дублирующих. Именно так действует естественное соединение.Слайд 25Реляционная модель данных.
Реляционная алгебра
Естественное соединение. Пусть даны отношения
A(A1,A2,…An,X1,X2,..Xp) и B(X1,X2,..Xp,B1,B2,…Bm) , имеющие одинаковые атрибуты (т.е. атрибуты с
одинаковыми именами и определенные на одинаковых доменах). Тогда естественным соединением отношений A и B называется отношение с заголовком (A1,A2,..An,X1,X2,..Xp,B1,B2,…Bm) и телом, содержащим множество кортежей , таких, что (a1,a2,…an,x1,x2,…xp) є A и (x1,x2,…xp,b1,b2,…bm) є B.Естественное соединение настолько важно, что для него используют специальный синтаксис: A JOIN B
Замечание 1. В синтаксисе естественного соединения не указываются, по каким атрибутам производится соединение. Естественное соединение производится по всем одинаковым атрибутам.
Слайд 26Реляционная модель данных.
Реляционная алгебра
Естественное соединение эквивалентно следующей последовательности
реляционных операций:
Переименовать одинаковые атрибуты в отношениях
Выполнить декартово произведение
отношений Выполнить выборку по совпадающим значениям атрибутов, имеющим одинаковые имена
Выполнить проекцию, удалив повторяющиеся атрибуты
Переименовать атрибуты, вернув им первоначальные имена
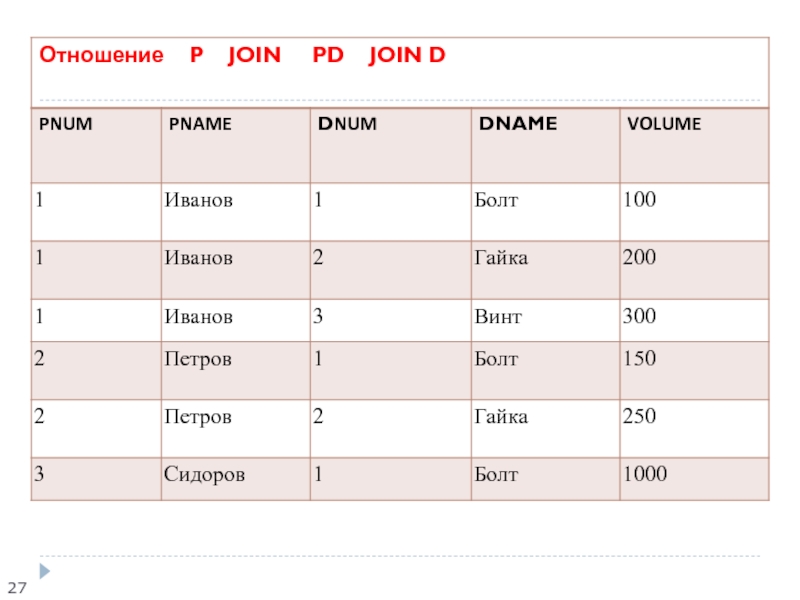
Пример 8 В предыдущем примере ответ на вопрос «Какие детали поставляются поставщиками?», более просто записывается в виде естественного соединения трех отношений P JOIN PD JOIN D
(для удобства просмотра порядок атрибутов изменен, это является допустимым по свойствам отношений):
Слайд 28Реляционная модель данных.
Реляционная алгебра
8. Деление. У операции реляционного
деления два операнда - бинарное и унарное отношения. Результирующее отношение
состоит из одноатрибутных кортежей, включающих значения первого атрибута кортежей первого операнда таких, что множество значений второго атрибута (при фиксированном значении первого атрибута) совпадает со множеством значений второго операнда.Пусть даны отношения A(X1,X2,...Xn,Y1,Y2,..Ym) и B(Y1,Y2,..Ym) , причем атрибуты (Y1,Y2,..Ym) - общие для двух отношений.
Делением отношения A на B называется отношение с заголовком (X1,X2,...Xn) и телом, содержащим множество кортежей (x1,x2,…xn), таких, что для всех кортежей (y1,y2,…ym) є B в отношении A найдется кортеж (x1,x2,…xn, y1,y2,…ym).
Отношение A выступает в роли делимого, отношение B выступает в роли делителя. Деление отношений аналогично делению чисел с остатком.
Синтаксис операции деления: A DEVIDEBY B
Замечание. Типичные запросы, реализуемые с помощью операции деления, обычно в своей формулировке имеют слово «все» - «Какие поставщики поставляют все детали?».
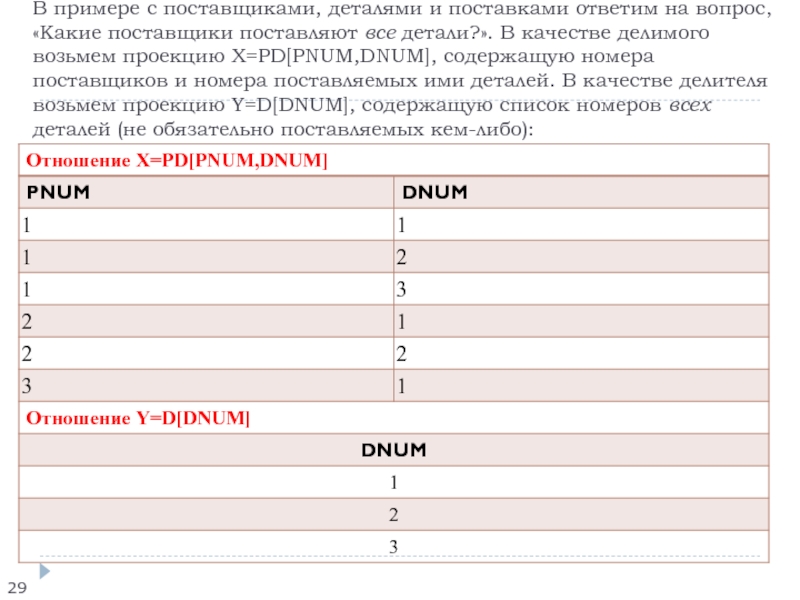
Слайд 29Пример 9 В примере с поставщиками, деталями и поставками
ответим на вопрос, «Какие поставщики поставляют все детали?». В качестве
делимого возьмем проекцию X=PD[PNUM,DNUM], содержащую номера поставщиков и номера поставляемых ими деталей. В качестве делителя возьмем проекцию Y=D[DNUM], содержащую список номеров всех деталей (не обязательно поставляемых кем-либо):Слайд 30Реляционная модель данных.
Реляционная алгебра
Деление дает список номеров поставщиков,
поставляющих все детали:
Отношение X DEVIDEBY Y
Номер поставщика
PNUM
1
Оказалось,
что только поставщик с номером 1 поставляет все детали.9. Переименование. Операция переименования производит отношение, тело которого совпадает с телом операнда, но имена атрибутов изменены.
10. Присваивание. Операция присваивания позволяет сохранить результат вычисления реляционного выражения в существующем отношении БД.
Слайд 31Реляционная модель данных.
Реляционная алгебра. Особенности операций реляционной алгебры
Совместимость
отношений по объединению (пересечению и взятию разности ): два отношения
совместимы по объединению в том и только в том случае, когда обладают одинаковыми заголовками. Более точно, это означает, что в заголовках обоих отношений содержится один и тот же набор имен атрибутов, и одноименные атрибуты определены на одном и том же домене.Если два отношения совместимы по объединению, то при обычном выполнении над ними операций объединения, пересечения и взятия разности результатом операции является отношение с корректно определенным заголовком, совпадающим с заголовком каждого из отношений-операндов. Напомним, что если два отношения «почти» совместимы по объединению, т.е. совместимы во всем, кроме имен атрибутов, то до выполнения операции типа соединения эти отношения можно сделать полностью совместимыми по объединению путем применения операции переименования.
Заметим, что включение в состав операций реляционной алгебры трех операций объединения, пересечения и взятия разности является очевидно избыточным, поскольку известно, что любая из этих операций выражается через две других.
Слайд 32Реляционная модель данных.
Реляционная алгебра
Все четыре теоретико-множественные операции являются
ассоциативными. Если обозначить через OP любую из четырех операций, то
(A OP B) OP C = A ОР (B OP C), и следовательно, без введения двусмысленности можно писать A OP B OP C (A, B и C - отношения, обладающие свойствами, требуемыми для корректного выполнения соответствующей операции).
Все операции, кроме взятия разности, являются коммутативными, т.е.
A OP B = B OP A.
Не все операции реляционной алгебры являются независимыми - некоторые из них выражаются через другие реляционные операции. Операция соединения определяется через операции декартового произведения и выборки. Для операции естественного соединения добавляется операция проекции. Операция пересечения выражается через вычитание следующим образом: A INTERSECT B = A MINUS (A MINUS B)
Операция деления выражается через операции вычитания, декартового произведения и проекции следующим образом:
A DEVIDEBY B=A[X] MINUS ((A[X] TIMES B) MINUS A)[X]
Несмотря на мощь языка реляционной алгебры, имеется ряд типов запросов, которые принципиально нельзя выразить только при помощи операций реляционной алгебры.
Слайд 33
Реляционная модель данных.
Реляционное исчисление
Пример 10 Предположим, что мы
работаем с базой данных, состоящей из двух отношений:
СОТРУДНИКИ (СОТР_НОМ,
СОТР_ИМЯ, СОТР_ЗАРП, ОТД_НОМ) и ОТДЕЛЫ (ОТД_НОМ, ОТД_КОЛ, ОТД_НАЧ), и хотим узнать имена и номера сотрудников, являющихся начальниками отделов с количеством сотрудников больше 50. Если бы для формулировки такого запроса использовалась реляционная алгебра, то мы получили бы алгебраическое выражение, которое читалось бы, например, следующим образом:
выполнить соединение отношений СОТРУДНИКИ и ОТДЕЛЫ по условию СОТР_НОМ = ОТД_НАЧ;
ограничить полученное отношение по условию ОТД_КОЛ > 50;
спроецировать результат предыдущей операции на атрибуты СОТР_ИМЯ, СОТР_НОМ.
Слайд 34
Реляционная модель данных.
Реляционное исчисление
Мы четко сформулировали последовательность шагов
выполнения запроса, каждый из которых соответствует одной реляционной операции.
Если
же сформулировать тот же запрос с использованием реляционного исчисления, то мы получили бы формулу, которую можно было бы прочитать, например, следующим образом: Выдать СОТР_ИМЯ и СОТР_НОМ для сотрудников таких, что существует отдел с таким же значением ОТД_НАЧ и значением ОТД_КОЛ большим 50. Во второй формулировке мы указали лишь характеристики результирующего отношения, но ничего не сказали о способе его формирования.
В этом случае система должна сама решить, какие операции и в каком порядке нужно выполнить над отношениями СОТРУДНИКИ и ОТДЕЛЫ. Обычно говорят, что алгебраическая формулировка является процедурной, т.е. задающей правила выполнения запроса, а логическая - описательной (или декларативной), поскольку она всего лишь описывает свойства желаемого результата. На самом деле эти два механизма эквивалентны и существуют не очень сложные правила преобразования одного формализма в другой.
Слайд 35
Реляционная модель данных.
Реляционное исчисление
Реляционное исчисление является прикладной ветвью
формального механизма исчисления предикатов первого порядка. Базисными понятиями исчисления являются
понятие переменной с определенной для нее областью допустимых значений и понятие правильно построенной формулы, опирающейся на переменные, предикаты и кванторы.Предикатом называется логическая функция, принимающая значения ИСТИНА или ЛОЖЬ в зависимости от значений входящих в нее переменных.
Различают исчисление кортежей и исчисление доменов. В исчислении кортежей областями определения переменных являются отношения базы данных, т.е. допустимым значением каждой переменной является кортеж некоторого отношения. В исчислении доменов областями определения переменных являются домены, на которых определены атрибуты отношений базы данных, т.е. допустимым значением каждой переменной является значение некоторого домена.
Рассмотрим более подробно исчисление кортежей, при этом будем использовать необходимые синтаксические конструкции, близкие синтаксису языка БД QUEL, который долгое время являлся основным языком СУБД Ingres.
Слайд 36
Реляционная модель данных.
Реляционное исчисление
Для определения кортежной переменной используется
оператор RANGE. Например, для того, чтобы определить переменную СОТРУДНИК, областью
определения которой является отношение СОТРУДНИКИ, нужно употребить конструкциюRANGE СОТРУДНИК IS СОТРУДНИКИ
Из этого определения следует, что в любой момент времени переменная СОТРУДНИК представляет некоторый кортеж отношения СОТРУДНИКИ. При использовании кортежных переменных в формулах можно ссылаться на значение атрибута переменной (это аналогично тому, как, например, при программировании на языке Паскаль можно сослаться на значение поля записи). Например, для того, чтобы сослаться на значение атрибута СОТР_ИМЯ переменной СОТРУДНИК, нужно употребить конструкцию СОТРУДНИК.СОТР_ИМЯ.
Слайд 37
Реляционная модель данных.
Реляционное исчисление
Правильно построенные формулы (ППФ) служат
для выражения условий, накладываемых на кортежные переменные.
Основой ППФ являются
простые сравнения, представляющие собой операции сравнения скалярных значений (значений атрибутов переменных или литерально заданных констант). Например, конструкция "СОТРУДНИК.СОТР_НОМ = 140" является простым сравнением. По определению, простое сравнение является ППФ, а ППФ, заключенная в круглые скобки, является простым сравнением. Более сложные варианты ППФ строятся с помощью логических связок NOT, AND, OR и IF ... THEN. Так, если form - ППФ, а comp - простое сравнение, то NOT form, comp AND form, comp OR form и IF comp THEN form являются ППФ.
Слайд 38
Реляционная модель данных.
Реляционное исчисление
Наконец, допускается построение ППФ с
помощью кванторов. Если form – это ППФ, в которой участвует
переменная var, то конструкцииEXISTS var (form) и FORALL var (form) представляют ППФ.
Все переменные, входящие в ППФ, при построении которой не использовались кванторы, являются свободными. Если имя переменной использовано сразу после квантора при построении ППФ вида EXISTS var (form) или FORALL var (form), то var –это связанная переменная.
ППФ F1: EXISTS СОТР2 (СОТР1. СОТР_ЗАРП> СОТР2. СОТР_ЗАРП) , где СОТР1 и СОТР2 – кортежные переменные. ППФ для текущего значения кортежа СОТР1 принимает значение true в том и только в том случае, если во всем отношении СОТРУДНИКИ найдется кортеж (связанный с переменной СОТР2) такой, что значение его атрибута СОТР_ЗАРП удовлетворяет условию.
ППФ F2 : FORALL СОТР2 (СОТР1. СОТР_ЗАРП> СОТР2. СОТР_ЗАРП)
ППФ для текущего значения кортежа СОТР1 принимает значение true в том и только в том случае, если для всех кортежей отношения СОТРУДНИКИ (связанных с переменной СОТР2) значение атрибута СОТР_ЗАРП удовлетворяют условию сравнения.
Слайд 39
Реляционная модель данных.
Вопросы
Чем отличается домен от типа данных?
Что такое
степень отношения?
В чем отличие схемы отношения от отношения?
Можно ли считать
любую прямоугольную таблицу данных отношением?В чем, по вашему мнению, основа популярности реляционной модели?
Приведите пример БД и укажите, какие ограничения целостности в ней должны поддерживаться.
Какие из реляционных операций взяты из теории множеств?
В чем заключается замкнутость реляционной алгебры?
В чем заключается совместимость операндов по реляционному объединению (пересечению, разности)?
Для чего нужны реляционные операции присваивания, переименования?
Назовите виды соединений?
Укажите последовательность действий при выполнении эквисоединения.
Какая реляционная операция в чистом виде почти не выполняется?
На каком математическом аппарате основано реляционное исчисление?
Укажите последовательность реляционных операций при выполнении запроса для БД примера 3.11 «Выбрать начальников отделов, заработная плата которых превышает 10000 рублей»
Задайте формулу реляционного исчисления для реализации запроса (БД примера 10 ) «Выбрать начальников отделов, заработная плата которых превышает 10000 рублей».
Слайд 40
Элементы языка SQL
История языка SQL
Увеличение объема и структурной сложности хранимых
данных, расширение круга пользователей информационных систем привели к широкому распространению
наиболее удобных реляционных (табличных) СУБД. Для обеспечения одновременного доступа к данным множества пользователей, нередко расположенных достаточно далеко друг от друга и от места хранения баз данных, созданы сетевые мультипользовательские версии СУБД. В них тем или иным путем решаются специфические проблемы параллельных процессов, целостности (правильности) и безопасности данных, а также санкционирования доступа. Совместная работа пользователей в сетях с помощью унифицированных средств общения с БД возможна только при наличии стандартного языка манипулирования данными, обладающего средствами для реализации перечисленных выше возможностейРазрабатываемые в начале 80-х языки запросов можно отнести к двум классам:
Алгебраические языки, позволяющие выражать запросы средствами специализированных операторов, применяемых к отношениям (JOIN - соединить, INTERSECT - пересечь, SUBTRACT - вычесть и т.д.).
Языки исчисления предикатов представляют собой набор правил для записи выражения, определяющего новое отношение из заданной совокупности существующих отношений
Слайд 41
Элементы языка SQL
История языка SQL
Разработка, в основном, шла в отделениях
фирмы IBM (языки ISBL, SQL, QBE) и университетах США (PIQUE,
QUEL). QUEL создавался для СУБД INGRES (Interactive Graphics and Retrieval System), которая была разработана в начале 70-х годов в Университете шт. Калифорния и сегодня входит в пятерку лучших профессиональных СУБД.Сегодня из всех этих языков полностью сохранились и развиваются QBE (Query-By-Example - запрос по образцу) и SQL, а из остальных взяты в расширение внутренних языков СУБД только наиболее интересные конструкции.
SQL был разработан в 1974 году фирмой IBM для экспериментальной реляционной СУБД System R. После появления на рынке двух пионерских СУБД этой фирмы - SQL/DS (1981 год) и DB2 (1983 год) - он приобрел статус стандарта де-факто для профессиональных реляционных СУБД.
Слайд 42
Элементы языка SQL
История языка SQL
Первый международный стандарт SQL был принят
в 1989 г. (SQL/89 или SQL1). Стандарт был принят ANSI
(Американский Национальный Институт Стандартов) и ISO (международная организация по стандартизации).Следующая версия стандарта языка SQL принята в 1992 г. (Официальное название стандарта - Международный стандарт языка баз данных SQL (1992) (International Standart Database Language SQL), неофициальное название - SQL/92, или SQL-92, или SQL2). Документ, описывающий стандарт, содержит более 600 страниц. Рассмотрим только некоторые основные понятия языка.
Далее был разработан SQL/99 или SQL3, принятый стандарт объектно-реляционного расширения SQL. Подмножества этого стандарта уже реализованы в коммерческих продуктах, включая Oracle V8 компании Oracle и DB2 корпорации IBM.
Слайд 43
Элементы языка SQL
История языка SQL
Язык SQL стал фактически стандартным языком
доступа к базам данных. Все СУБД, претендующие на название «реляционные»,
реализуют тот или иной диалект SQL: SQL*Plus корпорации Oracle; Transact-SQL для СУБД Microsoft SQL Server и др.В диалектах язык может быть дополнен операторами процедурных языков программирования. Многие системы, не являющиеся реляционными, также имеют в настоящее время средства доступа к реляционным данным. Целью стандартизации является переносимость приложений между различными СУБД.
Нужно заметить, что в настоящее время, ни одна система не реализует стандарт SQL в полном объеме. Кроме того, во всех диалектах языка имеются возможности, не являющиеся стандартными. Таким образом, можно сказать, что каждый диалект - это надмножество некоторого подмножества стандарта SQL. Это затрудняет переносимость приложений, разработанных для одних СУБД, в другие СУБД.
Имеются две формы языка SQL: интерактивный и вложенный.
В интерактивной форме SQL любая введенная команда выполнится сразу же и можно увидеть результаты работы команды.
Вложенный SQL состоит из команд SQL, встроенных внутрь программ, написанных на некотором другом языке (типа Visual Basic или С). В этой главе будет представлен SQL в интерактивной форме. Интерактивный SQL - это форма, наиболее полезная непрограммистам. Все что, рассмотрим относительно интерактивного SQL, в основном, применимо и к вложенной форме.
Слайд 44
Элементы языка SQL
История языка SQL
В настоящее время наибольшее распространение получили
реляционные СУБД трех групп:
Мощные крупные коммерческие СУБД, ориентированные на хранение
огромных объемов информации (от гигабайт). Наиболее известными СУБД в этой группе являются: Oracle (Oracle Corp.), Ingres (Computer Associates International), Sybase SQL server (Sybase Inc.).Мобильные компактные свободно распространяемые СУБД, использование которых оправдано и для БД объемом всего лишь в десятки килобайт. К наиболее популярным СУБД этой группы относятся: PostgreSQL (организации PostgreSQL), mySQL (T.C.X. DataKonsult AB), Microsoft SQL Server (Microsoft).
Настольные персональные СУБД, ориентированные на простые варианты построения БД, решение менее сложных задач, на персональные компьютеры и, на меньшие объемы и сравнительно простую структуру данных. К настольным СУБД относятся: Access, входящая в состав пакета Microsoft Office и рассчитанная на одного пользователя; Visual FoxPro.
СУБД первых двух групп построены по принципу «клиент-сервер».
Слайд 45
Элементы языка SQL
Структура языка SQL
Основу языка SQL составляют операторы, условно
разбитые на несколько групп по выполняемым функциям. Можно выделить следующие
группы операторов (перечислены не все операторы SQL):DDL (Data Definition Language) - операторы определения объектов базы данных:
CREATE SCHEMA - создать схему базы данных;
DROP SHEMA - удалить схему базы данных;
CREATE DATABASE - создать базы данных;
DROP DATABASE - удалить базу данных;
CREATE TABLE - создать таблицу;
ALTER TABLE - изменить таблицу;
DROP TABLE - удалить таблицу;
CREATE DOMAIN - создать домен;
ALTER DOMAIN - изменить домен;
DROP DOMAIN - удалить домен;
CREATE INDEX - создать индекс;
DROP INDEX - удалить индекс;
CREATE VIEW - создать представление;
DROP VIEW - удалить представление.
Слайд 46
Элементы языка SQL
Структура языка SQL
DML (Data Manipulation Language) - операторы
манипулирования данными:
SELECT - отобрать строки из таблиц;
INSERT - добавить
строки в таблицу; UPDATE - изменить строки в таблице;
DELETE - удалить строки в таблице;
DCL (Data Control Language) - операторы контроля данных, защиты и управления данными:
CREATE ASSERTION - создать ограничение;
DROP ASSERTION - удалить ограничение;
COMMIT - зафиксировать внесенные изменения;
ROLLBACK - откатить внесенные изменения.
GRANT - предоставить привилегии пользователю или приложению на манипулирование объектами;
REVOKE - отменить привилегии пользователя или приложения.
Слайд 47
Элементы языка SQL
Структура языка SQL
В языке SQL/89 поддерживаются следующие типы
данных :
CHARACTER(n) или CHAR(n) символьные строки с постоянной
длиной nNUMERIC[(n,m)], DECIMA[(n,m)] или DEC[(n,m)] точные числа, здесь n – общее число цифр в числе; m – количество цифр слева от десятичной точки
INTEGER или INT - целые числа
SMALLINT - целые числа меньшего диапазона
REAL - вещественные числа в форме с плавающей точкой
FLOAT[(n)] - вещественные числа большой точности в форме с плавающей точкой, здесь n – общее число байт, отводимое на хранение чисел
DOUBLE PRECISION - вещественные числа большой точности в форме с плавающей точкой
В стандарте SQL/92 добавлены типы данных:
VARCHAR(n) – строки символов переменной длины;
BIT(n) – строки битов постоянной длины;
DATE – календарная дата;
INTERVAL – временной интервал и др.
Слайд 48
Элементы языка SQL
Структура языка SQL
Заметим еще, что в большинстве реализаций
SQL поддерживаются некоторые дополнительные типы данных, например, TIME, INTERVAL, MONEY.
Некоторые из этих типов специфицированы в стандарте SQL/92, но в текущих реализациях синтаксические и семантические свойства таких типов могут различаться.Конкретными реализациями SQL поддерживаются собственные наборы типов данных и встроенных функций, позволяющих выполнять обработку данных числового и строкового типов. Определены арифметические операции: + | - | * | /
В качестве удобного примера при дальнейшем рассмотрении реализации операторов SQL будем использовать учебную БД условной торговой фирмы «ЗАКАЗЫ» (пример взят у М. Грабера [3]).
БД состоит из трех таблиц:
Таблица Продавцы :
номер продавца – SNUM;
имя продавца – SNAME;
город, в котором он живет, - CITY;
комиссионные, которые он получает с каждого оформленного заказа, - COMM.
Слайд 49
Элементы языка SQL
Структура языка SQL
Таблица Заказчики :
номер заказчика –
CNUM;
имя заказчика – CNAME;
город, в котором он живет,
- CITY; номер продавца, который обслуживает данного заказчика, - SNUM;
оценка заказчика – rating.
Таблица Заказы (здесь они названы порядками):
номер заказа – ONUM;
сумма заказа – AMT;
дата оформления заказа – ODATE;
номер заказчика, который оплатил данный заказ, - CNUM;
номер продавца, который обслуживает данный заказ, - SNUM.
Приняты следующие соглашения (бизнес-правила):
один продавец может обслуживать несколько заказчиков;
один заказчик работает только с одним продавцом данной фирмы.















![БАЗЫ ДАННЫХ Ответ на вопрос, какие детали поставляются поставщиками, дает эквисоединение P[PNUM=PNUM] Ответ на вопрос, какие детали поставляются поставщиками, дает эквисоединение P[PNUM=PNUM] PD. На самом деле, т.к. в](/img/thumbs/6935ab6293cce5581b197aa658cdf45e-800x.jpg)