Лекция 1 Тема : Виды сигналов и формы их описания

и формы их описания.
Статистические и обобщённые характеристики сигналов.

процессов.
Формы представления сигналов.
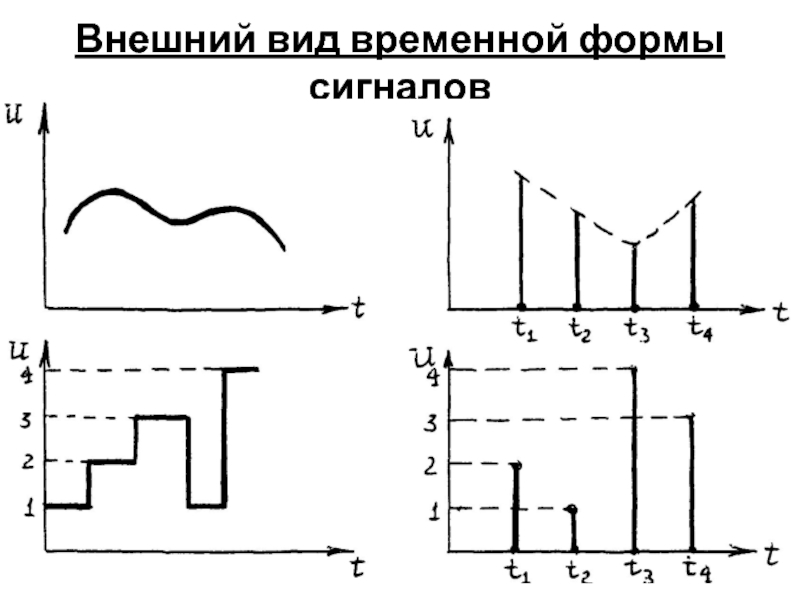
Внешний вид временной формы сигналов.
Виды представления сигналов.
Разложение периодического

сигнала в ряд Фурье.
Спектральные линии и диаграммы.
Комплексная форма ряда Фурье.
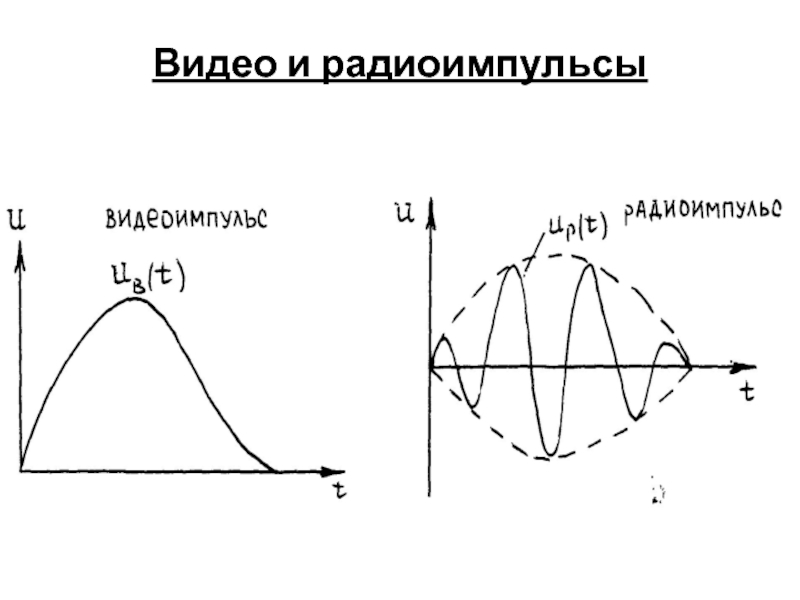
Видео и радиоимпульсы.
Спектр импульсного непериодического сигнала.
Прямое и обратное преобразование Фурье.
Теорема Котельникова.

Для передачи информации, заложенной в сообщениях, на большие расстояния используют

сигналы.
Под сигналами в широком смысле понимают материальные носители информации.
В узком смысле под сигналом понимают конкретный физический процесс, отражающий полезное сообщение и способный распространяться от источника к получателю сообщений с конечной скоростью.

времени;
в) дискретный сигнал непрерывного времени;
г) дискретный сигнал дискретного времени.

и спектральное представление детерминированных сигналов.
Временная форма представления позволяет определить:
-длительность
-мощность
энергию сигнала.
Для

согласования сигнала с каналом связи наиболее важной характеристикой сигнала является ширина его спектра.
Временное и спектральное представление сигналов связаны между собой с помощью преобразования Фурье.

на простейшие гармонические колебания производится с помощью ряда Фурье, тригоно-

метрическая форма которого имеет вид:

гармоник называются спектральными диаграммами сигнала, а линии, соответствующие амплитудам и

фазам гармоник, называются спектральными линиями.
Закон распределения амплитуд Sk составляющих периодического сигнала по частоте называется спектром амплитуд этого сигнала, а закон распределения фаз φk - спектром фаз.
Если нас интересует не значения амплитуд и начальных фаз гармоник, то говорят о спектре частот сигнала.
Если спектр периодического сигнала состоит из отдельных спектральных линий, то его называют дискретным.

его условно превращают в периодический с произвольным периодом .
Устремляя

к в пределе получаются бесконечно малые амплитуды гармонических составляющих, разложенных на всех частотах.
Количество гармоник будет бесконечно большим, т.к. при основная частота .
Расстояние между спектральными линиями, равное частоте становится бесконечно малым, а спектр – сплошным.
В частотной области непериодические колебания описываются спектральной плотностью или спектральной функцией.

это осуществляют с помощью теоремы Котельникова:
Любая функция времени S(t), описывающая

непрерывный сигнал, спектр которого ограничен частотой Fc, определяется последовательностью своих мгновенных значений, отсчитанных через интервалы ,

где
Fc верхняя частота в спектре сигнала.
Если на интервале Tc функция существует, то она может быть отобра- жена 2·Tc·Fc отсчетами, расположенными на расстоянии Δt друг от друга и образующими сигнальную кодовую группу. Это применяется и к функциям, которых спектр неограничен, но быстро убывает за преде- лами Fc.
Функция может быть восстановлена по её отсчётам с легко оценива- емым приближением.

показатели сигнала.
Квант сигнала.

, где Т - время наблюдения случайного процесса;
2) Средняя мощность,

которую развивает случайный сигнал S(t) на резисторе, сопротивлением 1 Ом в момент t ,

3)энергетический спектр
, где
Bτ - корреляционная функция, устанавливающая связь между значениями случайного сигнала S(t) в различные моменты времени t1 и t2.


Функция G(ω) - это спектральная плотность средней мощности процесса, т.е. мощности заключённой в бесконечно малой полосе частот.
4) Мощность, заключённая в конечной полосе частот между ω1 и ω2
 

, характеризующей его мощность
Vc = Tc · Fc ·

Ac
Vc - объём сигнала

всегда имеет место пороговое значение параметров сигнала
Δ Tc , Δ

Fc , Δ Ac - они характеризуют минимально различимую величину сигнала.
Δ Vc = Δ Tc · Δ Fc · Δ Ac - это квант сигнала
Δ Sc = Δ Tc · Δ Fc - элементарная площадь сигнала
Элементарной площади Δ S соответствует только один квант Δ Vc , определяемый пороговым значением сигнала.
Tc и Fc - это независимые переменные;
Ac - характеризует мощность сигнала и является зависимой величиной;
Δ Ac - определяется значением помехи;
Δ Ac - это минимальная мощность сигнала.

где
Pn - средняя мощность помехи
mp - коэффициент различимости сигнала.
На практике

mp трудно оценить, поэтому вводят и используют превышение сигнала над помехой:

Объём сигнала:
Vc = Tc · Fc · Hc
 
Для канала:
Vk = Tk · Fk · Hk