Слайд 1Булевы функции
Минимизация БФ
Слайд 5Алгоритм построения МДНФ
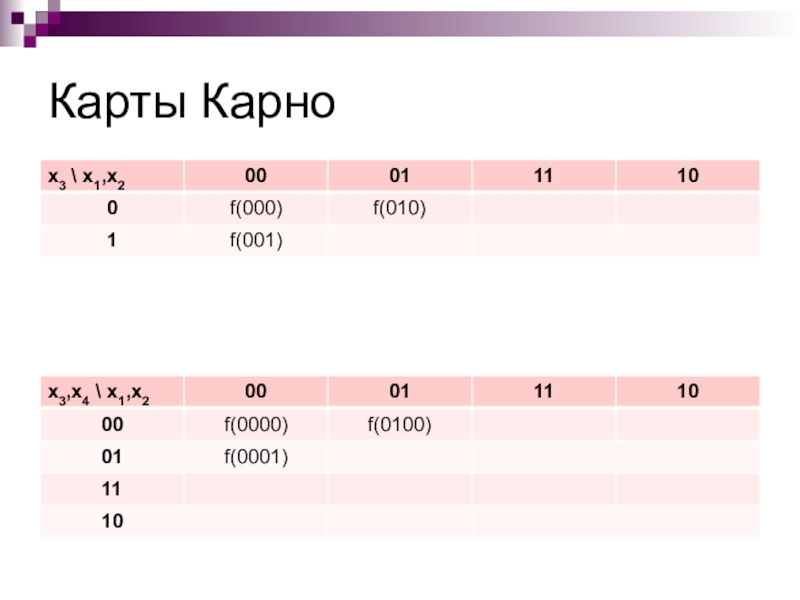
На карте Карно покрыть все «1» минимально возможным
количеством прямоугольников. Площадь каждого прямоугольника должна быть максимально возможной, стороны
равны 1, 2 или 4. Каждая «1» может быть покрыта несколькими прямоугольниками. Края карты Карно «склеены» в тор!
Для каждого прямоугольника записать «слагаемое»
В каждом «слагаемом» присутствует произведение переменных, которые не меняются в рамках прямоугольника. Причем если переменная равна 0, то переменная присутствует с отрицанием, иначе (если равна 1), то без отрицания
Между «слагаемыми» поставить знак дизъюнкции V
Слайд 7Алгоритм построения МКНФ
На карте Карно покрыть все «0» минимально возможным
количеством прямоугольников. Площадь каждого прямоугольника должна быть максимально возможной, стороны
равны 1, 2 или 4. Каждый «0» может быть покрыт несколькими прямоугольниками. Края карты Карно «склеены» в тор!
Для каждого прямоугольника записать «множитель»
В каждом «множителе» присутствует логическая сумма переменных, которые не меняются в рамках прямоугольника. Причем если переменная равна 1, то переменная присутствует с отрицанием, иначе (если равна 0), то без отрицания
Между «множителями» поставить знак конъюнкции &
Слайд 9Булевы функции
Замкнутые классы БФ
Слайд 10Замкнутые классы
Класс (множество) булевых функций называется замкнутым, если любая суперпозиция
функций из этого множества также принадлежит этому же множеству
Слайд 11Замкнутые классы
T0 – класс функций, сохраняющих 0, то есть при
всех аргументах, равных 0, значение функции тоже равно 0
Утв. 1.1.
Класс T0 – замкнутый
Утв. 1.2. О количестве функций в T0
Слайд 12Замкнутые классы
T1 – класс функций, сохраняющих 1, то есть при
всех аргументах, равных 1, значение функции тоже равно 1
Утв. 2.1.
Класс T1 – замкнутый
Утв. 2.2. О количестве функций в T1
Слайд 13Проверка посещаемости.
ПМИ-1,2 и ПМИ-3,4
Голосование:
ПМИ-1
ПМИ-2
ПМИ-3
ПМИ-4
Слайд 14Проверка посещаемости.
ПМИ-5,6 и ПМИ-7,8
Голосование:
ПМИ-5
ПМИ-6
ПМИ-7
ПМИ-8