Слайд 1Chap 4-
Chapter 4
Basic Probability
Business Statistics: A First Course
6th Edition
Слайд 2Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Learning Objectives
In this chapter, you learn:
Basic probability concepts
Conditional probability
To use Bayes’ theorem to revise probabilities
Various counting rules
Слайд 3Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Basic Probability Concepts
Probability – the chance that an uncertain event
will occur (always between 0 and 1)
Impossible Event – an event that has no chance of occurring (probability = 0)
Certain Event – an event that is sure to occur (probability = 1)
Слайд 4Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Assessing Probability
There are three approaches to assessing the probability of
an uncertain event:
1. a priori -- based on prior knowledge of the process
2. empirical probability -- based on observed data
3. subjective probability
based on a combination of an individual’s past experience, personal opinion, and analysis of a particular situation
Assuming all outcomes are equally likely
probability of occurrence
probability of occurrence
Слайд 5Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Example of a priori probability
When randomly selecting a day from
the year 2012 what is the probability the day is in January?
Слайд 6Business Statistics: A First Course.
Chap 4-
Example of a priori probability
Find
the probability of selecting a face card (Jack, Queen, or
King) from a standard deck of 52 cards.
Слайд 7Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Example of empirical probability
Find the probability of selecting a male
taking statistics from the population described in the following table:
Probability of male taking stats
Слайд 8Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Events
Each possible outcome of a variable is an event.
Simple event
An
event described by a single characteristic
e.g., A day in January from all days in 2012
Joint event
An event described by two or more characteristics
e.g. A day in January that is also a Wednesday from all days in 2012
Complement of an event A (denoted A’)
All events that are not part of event A
e.g., All days from 2012 that are not in January
Слайд 9Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
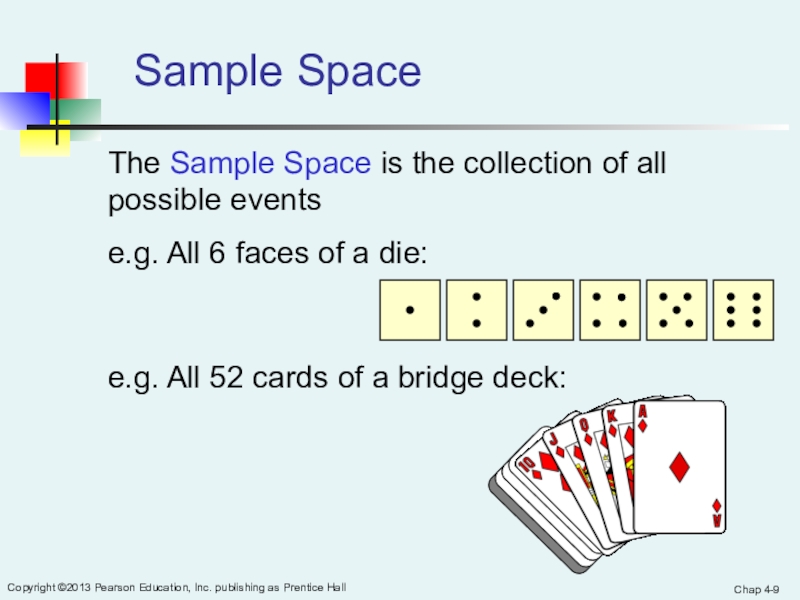
Sample Space
The Sample Space is the collection of all
possible events
e.g. All 6 faces of a die:
e.g. All 52 cards of a bridge deck:
Слайд 10All 52 cards of a bridge deck
Chap 4-
Слайд 11Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
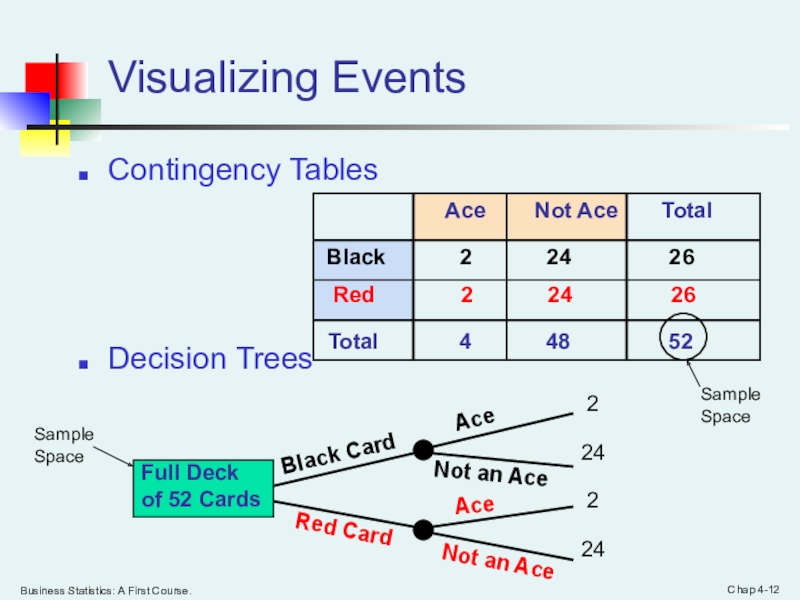
Visualizing Events
Contingency Tables -- For All Days in 2012
Decision Trees
All
Days
In 2012
Not Jan.
Jan.
Not Wed.
Wed.
Wed.
Not Wed.
Sample Space
Total
Number
Of
Sample
Space
Outcomes
4
27
48
287
Слайд 12Business Statistics: A First Course.
Chap 4-
Visualizing Events
Contingency Tables
Decision
Trees
Red 2
24 26
Black 2 24 26
Total 4 48 52
Ace Not Ace Total
Full Deck
of 52 Cards
Red Card
Black Card
Not an Ace
Ace
Ace
Not an Ace
Sample Space
Sample Space
2
24
2
24
Слайд 13Business Statistics: A First Course.
Chap 4-
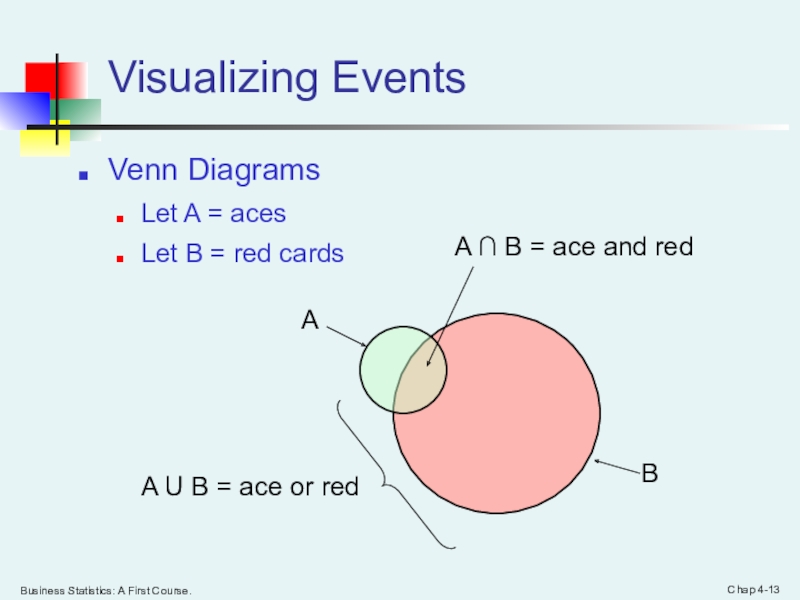
Visualizing Events
Venn Diagrams
Let A
= aces
Let B = red cards
A
B
A ∩ B = ace
and red
A U B = ace or red
Слайд 14Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Definition: Simple Probability
Simple Probability refers to the probability of a
simple event.
ex. P(Jan.)
ex. P(Wed.)
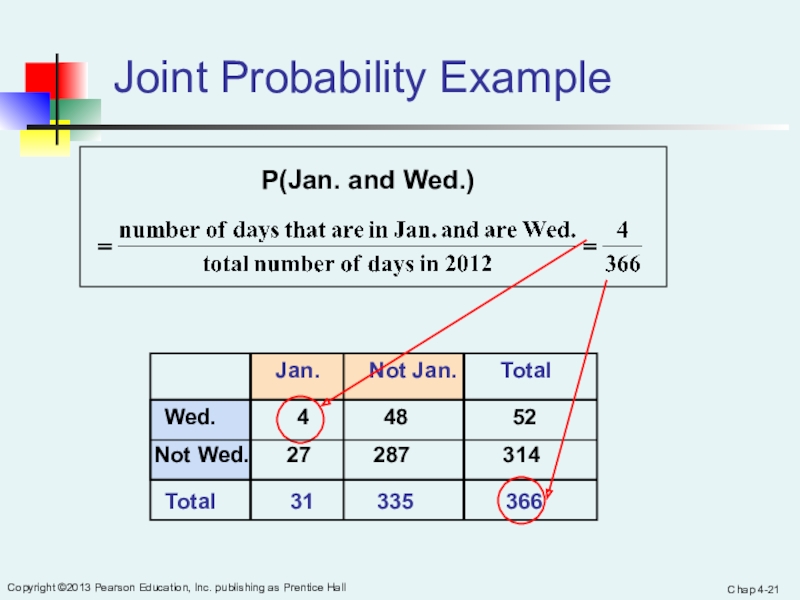
P(Jan.) = 31 / 366
P(Wed.) = 52 / 366
Not Wed. 27 287 314
Wed. 4 48 52
Total 31 335 366
Jan. Not Jan. Total
Слайд 15Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Definition: Joint Probability
Joint Probability refers to the probability of an
occurrence of two or more events (joint event).
ex. P(Jan. and Wed.)
ex. P(Not Jan. and Not Wed.)
P(Jan. and Wed.) = 4 / 366
P(Not Jan. and Not Wed.)
= 287 / 365
Not Wed. 27 287 314
Wed. 4 48 52
Total 31 335 366
Jan. Not Jan. Total
Слайд 16Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Mutually Exclusive Events
Mutually exclusive events
Events that cannot occur simultaneously
Example: Randomly
choosing a day from 2010
A = day in January; B = day in February
Events A and B are mutually exclusive
Слайд 17Business Statistics: A First Course.
Chap 4-
Mutually Exclusive Events
Example: Drawing
one card from a deck of cards
A = queen
of diamonds; B = queen of clubs
Events A and B are mutually exclusive
Слайд 18Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Collectively Exhaustive Events
Collectively exhaustive events
One of the events must occur
The set of events covers the entire sample space
Example: Randomly choose a day from 2012
A = Weekday; B = Weekend;
C = January; D = Spring;
Events A, B, C and D are collectively exhaustive (but not mutually exclusive – a weekday can be in January or in Spring)
Events A and B are collectively exhaustive and also mutually exclusive
Слайд 19Business Statistics: A First Course.
Chap 4-
Collectively Exhaustive Events
Example:
A
= aces; B = black cards;
C = diamonds; D
= hearts
Events A, B, C and D are collectively exhaustive (but not mutually exclusive – an ace may also be a heart)
Events B, C and D are collectively exhaustive and also mutually exclusive
Слайд 20Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Computing Joint and
Marginal Probabilities
The probability of a joint event,
A and B:
Computing a marginal (or simple) probability:
Where B1, B2, …, Bk are k mutually exclusive and collectively exhaustive events
Слайд 21Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Joint Probability Example
P(Jan. and Wed.)
Слайд 22Business Statistics: A First Course.
Chap 4-
Joint Probability Example
P(Red and Ace)
Black
Color
Type
Red
Total
Ace
2
2
4
Non-Ace
24
24
48
Total
26
26
52
Слайд 23Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Marginal Probability Example
P(Wed.)
Слайд 24Business Statistics: A First Course.
Chap 4-
Marginal Probability Example
P(Ace)
Black
Color
Type
Red
Total
Ace
2
2
4
Non-Ace
24
24
48
Total
26
26
52
Слайд 25Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
P(A1 and B2)
P(A1)
Total
Event
Marginal & Joint Probabilities
In A Contingency Table
P(A2 and B1)
P(A1 and B1)
Event
Total
1
Joint Probabilities
Marginal (Simple) Probabilities
A1
A2
B1
B2
P(B1)
P(B2)
P(A2 and B2)
P(A2)
Слайд 26Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Probability Summary So Far
Probability is the numerical measure of the
likelihood that an event will occur
The probability of any event must be between 0 and 1, inclusively
The sum of the probabilities of all mutually exclusive and collectively exhaustive events is 1
Certain
Impossible
0.5
1
0
0 ≤ P(A) ≤ 1 For any event A
If A, B, and C are mutually exclusive and collectively exhaustive
Слайд 27Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
General Addition Rule
P(A or B) = P(A) + P(B) -
P(A and B)
General Addition Rule:
If A and B are mutually exclusive, then
P(A and B) = 0, so the rule can be simplified:
P(A or B) = P(A) + P(B)
For mutually exclusive events A and B
Слайд 28Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
General Addition Rule Example
P(Jan. or Wed.) = P(Jan.) + P(Wed.)
- P(Jan. and Wed.)
= 31/366 + 52/366 - 4/366 = 79/366
Don’t count the four Wednesdays in January twice!
Слайд 29Marble Example 1: A bag contains 4 white, 3 red,
2 black, 2 green, 1 yellow, and 0 blue marbles.
One marble is chosen at random. Determine the probability of each event.
1. P(green)=
2. P(blue)=
3. P (not white)=
4. P (red or black)=
General Addition Rule Example
Слайд 30Card Example: One card is randomly chosen from a standard
deck of 52 cards. Determine the probability of each event.
1. P(king)= 2. P(heart)=
3. P (face card)= 4. P (not a spade)=
5. P(king and heart)= 6. P(king or heart)=
7. P(10 and jack)= 8. P(10 or jack)=
9. P (diamond or face card)=
10. P (red card or queen)=
General Addition Rule Example
Слайд 31Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Computing Conditional Probabilities
A conditional probability is the probability of one
event, given that another event has occurred:
Where P(A and B) = joint probability of A and B
P(A) = marginal or simple probability of A
P(B) = marginal or simple probability of B
The conditional probability of A given that B has occurred
The conditional probability of B given that A has occurred
Слайд 32Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
What is the probability that a car has a GPS
given that it has AC ?
i.e., we want to find P(GPS | AC)
Conditional Probability Example
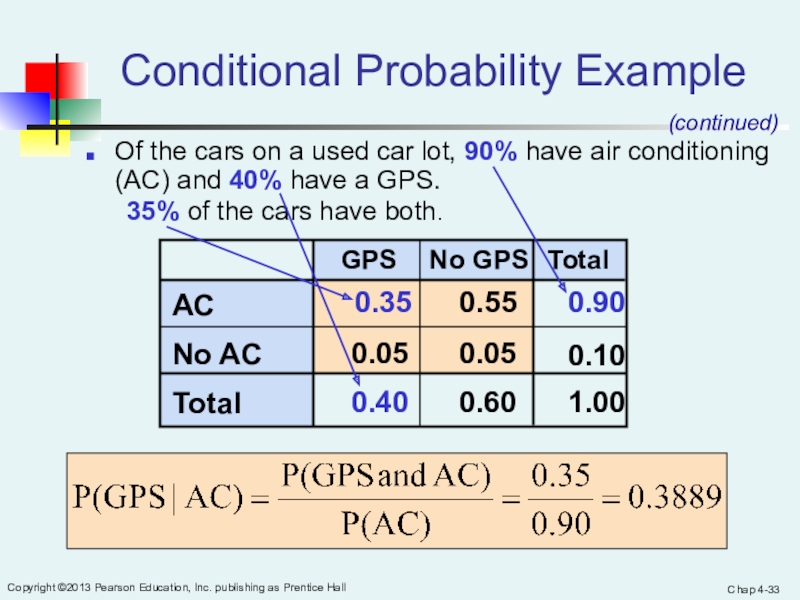
Of the cars on a used car lot, 90% have air conditioning (AC) and 40% have a GPS. 35% of the cars have both.
Слайд 33Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Conditional Probability Example
Of the cars on a used car lot,
90% have air conditioning (AC) and 40% have a GPS.
35% of the cars have both.
(continued)
Слайд 34Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
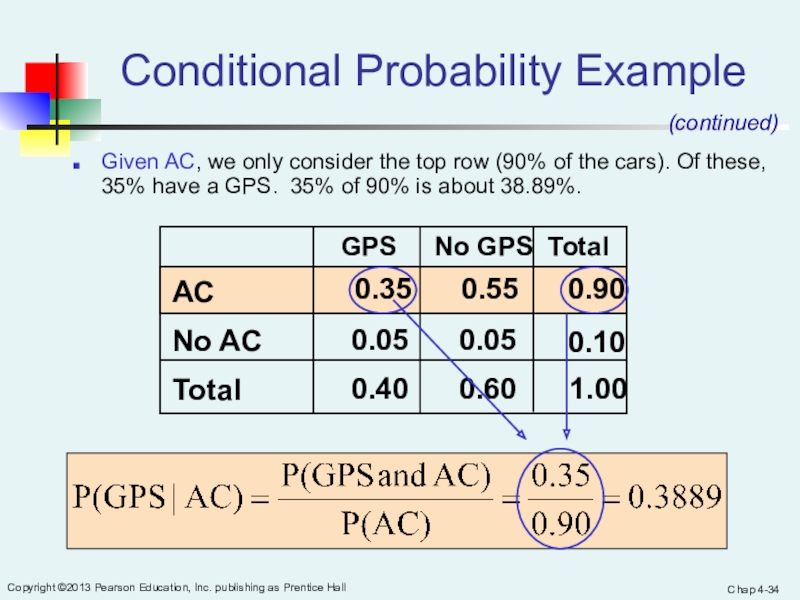
Conditional Probability Example
Given AC, we only consider the top row
(90% of the cars). Of these, 35% have a GPS. 35% of 90% is about 38.89%.
(continued)
No GPS
GPS
Total
AC
0.35
0.55
0.90
No AC
0.05
0.05
0.10
Total
0.40
0.60
1.00
Слайд 35Business Statistics: A First Course, 5e © 2009 Prentice-Hall, Inc.
Chap
4-
What is the probability that a car has a CD
player, given that it has AC ?
i.e., we want to find P(CD | AC)
Conditional Probability Example
Of the cars on a used car lot, 70% have air conditioning (AC) and 40% have a CD player (CD). 20% of the cars have both.
Слайд 36Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
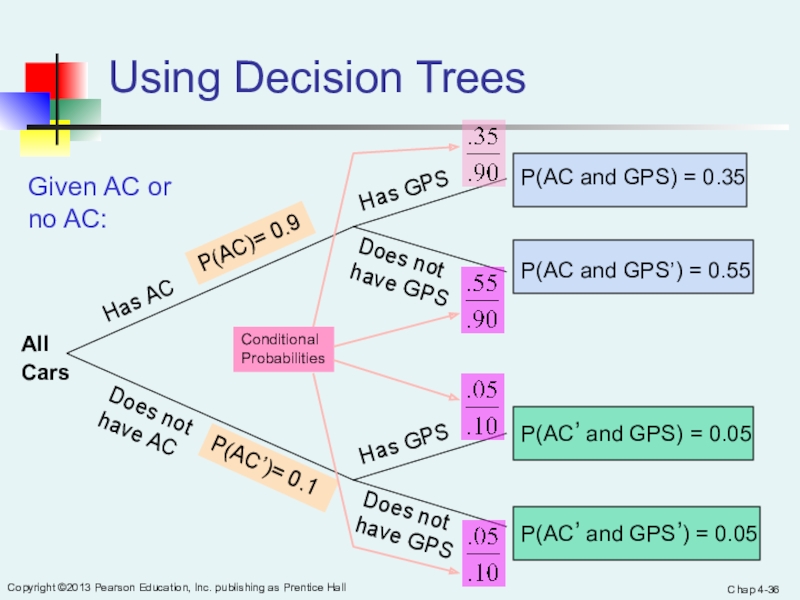
Using Decision Trees
Has AC
Does not have AC
Has GPS
Does not have
GPS
Has GPS
Does not have GPS
P(AC)= 0.9
P(AC’)= 0.1
P(AC and GPS) = 0.35
P(AC and GPS’) = 0.55
P(AC’ and GPS’) = 0.05
P(AC’ and GPS) = 0.05
All
Cars
Given AC or no AC:
Conditional
Probabilities
Слайд 37Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Using Decision Trees
Has GPS
Does not have GPS
Has AC
Does not have
AC
Has AC
Does not have AC
P(GPS)= 0.4
P(GPS’)= 0.6
P(GPS and AC) = 0.35
P(GPS and AC’) = 0.05
P(GPS’ and AC’) = 0.05
P(GPS’ and AC) = 0.55
All
Cars
Given GPS or no GPS:
(continued)
Conditional
Probabilities
Слайд 38Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Independence
Two events are independent if and only if:
Events A and
B are independent when the probability of one event is not affected by the fact that the other event has occurred
Слайд 39Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Multiplication Rules
Multiplication rule for two events A and B:
Note: If
A and B are independent, then
and the multiplication rule simplifies to
Слайд 40Multiplication Rules
Marble Example 2: A bag contains 4 white,
3 red, 2 black, 2 green, 1 yellow, and 0
blue marbles. One marble is chosen at random. It is replaced, and then another marble is randomly chosen. Determine the probability of each event.
1. P(green is chosen first and red is chosen second)=
2. P(black is chosen first and black is chosen second)=
3. P (green and red in either order)=
Слайд 41Multiplication Rules
Marble Example 3: A bag contains 4 white,
3 red, 2 black, 2 green, 1 yellow, and 0
blue marbles. One marble is chosen at random. It is not replaced, and then another marble is randomly chosen. Determine the probability of each event.
1. P(green is chosen first and red is chosen second)=
2. P(black is chosen first, and black is chosen second)=
Слайд 42Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Marginal Probability
Marginal probability for event A:
Where B1, B2, …, Bk
are k mutually exclusive and collectively exhaustive events
Слайд 43Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Bayes’ Theorem
Bayes’ Theorem is used to revise previously calculated probabilities
based on new information.
Developed by Thomas Bayes in the 18th Century.
It is an extension of conditional probability.
Слайд 44Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Bayes’ Theorem
where:
Bi = ith event of k mutually exclusive and
collectively
exhaustive events
A = new event that might impact P(Bi)
Слайд 45Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Bayes’ Theorem Example
A drilling company has estimated a 40% chance
of striking oil for their new well.
A detailed test has been scheduled for more information. Historically, 60% of successful wells have had detailed tests, and 20% of unsuccessful wells have had detailed tests.
Given that this well has been scheduled for a detailed test, what is the probability
that the well will be successful?
Слайд 46Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Let S = successful well
U = unsuccessful
well
P(S) = 0.4 , P(U) = 0.6 (prior probabilities)
Define the detailed test event as D
Conditional probabilities:
P(D|S) = 0.6 P(D|U) = 0.2
Goal is to find P(S|D)
Bayes’ Theorem Example
(continued)
Слайд 47Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Bayes’ Theorem Example
(continued)
Apply Bayes’ Theorem:
So the revised probability of success,
given that this well has been scheduled for a detailed test, is 0.667
Слайд 48Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Given the detailed test, the revised probability of a successful
well has risen to 0.667 from the original estimate of 0.4
Bayes’ Theorem Example
Sum = 0.36
(continued)
Слайд 49Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Counting Rules
Rules for counting the number of possible outcomes
Counting Rule
1:
If any one of k different mutually exclusive and collectively exhaustive events can occur on each of n trials, the number of possible outcomes is equal to
Example
If you roll a fair die 3 times then there are 63 = 216 possible outcomes
kn
Слайд 50Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Counting Rules
Counting Rule 2:
If there are k1 events on the
first trial, k2 events on the second trial, … and kn events on the nth trial, the number of possible outcomes is
Example:
You want to go to a park, eat at a restaurant, and see a movie. There are 3 parks, 4 restaurants, and 6 movie choices. How many different possible combinations are there?
Answer: (3)(4)(6) = 72 different possibilities
(k1)(k2)…(kn)
(continued)
Слайд 51Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Counting Rules
Counting Rule 3:
The number of ways that n items
can be arranged in order is
Example:
You have five books to put on a bookshelf. How many different ways can these books be placed on the shelf?
Answer: 5! = (5)(4)(3)(2)(1) = 120 different possibilities
n! = (n)(n – 1)…(1)
(continued)
Слайд 52Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Counting Rules
Counting Rule 4:
Permutations: The number of ways of arranging
X objects selected from n objects in order is
Example:
You have five books and are going to put three on a bookshelf. How many different ways can the books be ordered on the bookshelf?
Answer: different possibilities
(continued)
Слайд 53Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Counting Rules
Counting Rule 5:
Combinations: The number of ways of selecting
X objects from n objects, irrespective of order, is
Example:
You have five books and are going to randomly select three to read. How many different combinations of books might you select?
Answer: different possibilities
(continued)
Слайд 54Chap 4-
Copyright ©2013 Pearson Education, Inc. publishing as Prentice Hall
Chapter Summary
Discussed basic probability concepts
Sample spaces and events, contingency tables,
simple probability, and joint probability
Examined basic probability rules
General addition rule, addition rule for mutually exclusive events, rule for collectively exhaustive events
Defined conditional probability
Statistical independence, marginal probability, decision trees, and the multiplication rule
Discussed Bayes’ theorem
Discussed various counting rules