ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ОПЕРАТОРНЫЕ ФУНКЦИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

средством связи для передачи сигналов от источника сигнала в нагрузку

(рис. 5.1), где x(t) – сигнал на входе цепи, он называется входным сигналом, или воздействием; y(t) – выходной сигнал, или отклик:






В общем случае связь между откликом и воздействием имеет вид дифференциального уравнения. Если цепь линейная, то уравнение линейное, где a, b, c – параметры элементов, входящих в цепь.
Если входной сигнал гармонический, то его представляют комплексной амплитудой


Если цепь линейная, то откликом такой цепи является гармонический сигнал с комплексной амплитудой


Причем связь между комплексной амплитуды отклика и воздействия имеет вид линейного алгебраического уравнения:


где H (a, b, c) – комплексный параметр электрической цепи (это комплексное число).

Комплексным параметром цепи называют отношение комплексной амплитуды отклика к комп-лексной амплитуде воздействия.

Его режим работы характеризуется двумя величинами

.
1. Если воздействием считать амплитуду тока, то откликом будет являться напряжение на нем.
Тогда параметр .

Он имеет размерность сопротивления, Z – комплексное сопротивление двухполюсника. (Z = R+jX – комплексное число, где R и X – резистивная и реактивная составляющие сопротивления двухполюсника).Обобщенная схема замещения двухполюсника - рис. 5.3.
2. Если воздействием считаем амплитуду напряжения, тогда откликом будет амплитуда тока, связанная с напряжением, а параметр



где Y – второй параметр двухполюсника, он называется комплексной проводимостью двухполюсника: Y = G + jB, G и B – резистивная и реактивная составляющие проводимости двухполюсника.
Вторая схема замещения двухполюсника приведена на рис. 5.4. Эти схемы замещения при определенном выборе параметров эквивалентны.

5.5).
Параметры четырехполюсника можно разбить на четыре группы:
1. Входные параметры связывают

входные напряжение и ток. Их два :

:
, ,
где Zвх – входное сопротивление четырехполюсника; Yвх – входная проводимость четырехполюсника.
2. Передаточные параметры характеризуют передачу сигнала с входа на выход, или, как говорят, передачу в прямом направлении. Передаточных параметров четыре



где Ku – коэффициент передачи по напряжению;
Ki – коэффициент передачи по току;
Kiu – сопротивление прямой передачи, или коэффициент преобразования ток – напряжение;
Kui – проводимость прямой передачи, или коэффициент преобразования напряжение – ток.
3. Выходные параметры. Их два:


где Zвых – комплексное выходное сопротивление; комплексная выходная проводимость
– комплексная амплитуда выходного напряжения в режиме холостого хода (х.х).;
– комплексная амплитуда выходного тока в режиме короткого замыкания (к.з).

4. Параметры обратной передачи сигнала. Они характеризуют передачу сигнала с выхода на вход. Таких параметра четыре, и они аналогичны параметрам второй группы: (Ku, Ki, Kiu, Kui).

то параметры цепей оказываются частотно-зависимыми. Зависимости параметров цепей от частоты

называют частотными характеристиками (ЧХ) или частотными функциями цепи.
Каждый параметр цепи имеет свою частотную характеристику. Название ЧХ дают в соответствии с названием параметра, например ЧХ входного сопротивления, ЧХ коэффициента передачи напряжения.
ЧХ есть зависимость от частоты отношения комплексной амплитуды отклика к комплексной амплитуде воздействия. Как всякую комплексную функцию ее можно записать в одной из трех форм записи: показательной, алгебраической и тригонометрической (применяется редко).

Графики строят двумя способами.
1. В виде двух графиков –

АЧХ и ФЧХ.
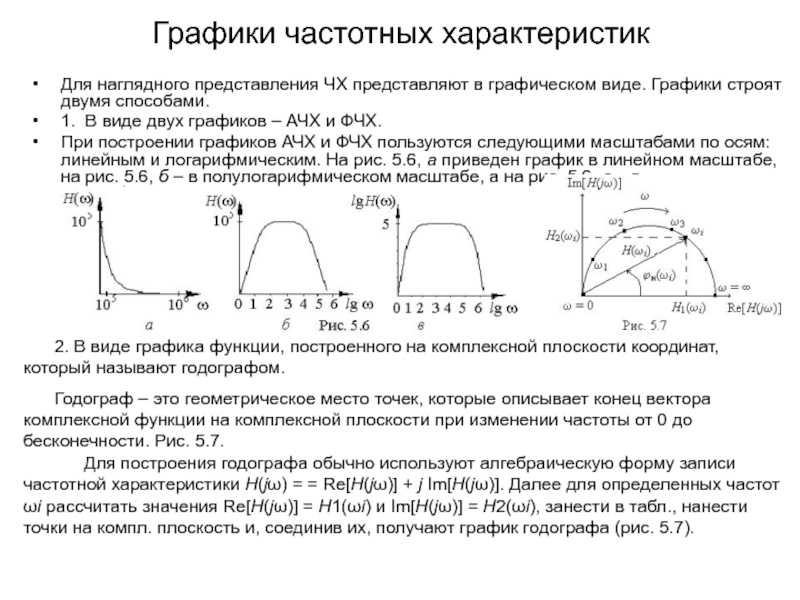
При построении графиков АЧХ и ФЧХ пользуются следующими масштабами по осям: линейным и логарифмическим. На рис. 5.6, а приведен график в линейном масштабе, на рис. 5.6, б – в полулогарифмическом масштабе, а на рис. 5.6, в – в логарифмическом.

2. В виде графика функции, построенного на комплексной плоскости координат, который называют годографом.
Годограф – это геометрическое место точек, которые описывает конец вектора комплексной функции на комплексной плоскости при изменении частоты от 0 до бесконечности. Рис. 5.7.
Для построения годографа обычно используют алгебраическую форму записи частотной характеристики Н(jω) = = Re[Н(jω)] + j Im[Н(jω)]. Далее для определенных частот ωi рассчитать значения Re[Н(jω)] = Н1(ωi) и Im[Н(jω)] = Н2(ωi), занести в табл., нанести точки на компл. плоскость и, соединив их, получают график годографа (рис. 5.7).

цепи, представленной комплексной схемой замещения (рис. 5.8),
рассчитать ее основные

частотные характеристики:
1. КЧХ - Zвх(j), АЧХ - Zвх(), ФЧХ - Z() - входного сопротивления;
2. КЧХ - K(j), АЧХ - K(),ФЧХ - K() - коэффициента передачи напряжений.

работы) условие, при котором цепь, содержащая реактивные элементы (L и

C), имеет резистивное входное сопротивление, т.е. при резонансе ток и напряжение находятся в одной фазе, а сдвиг по фазе равен нулю.
Такой резонанс называют фазовым.
Условие фазового резонанса: φ(ω0)=0 или X(ω0)=0 или G(ω0)=0,
где ω0ф –резонансная частота.
В информационной технике под резонансом чаще понимают амплитудный резонанс. Это такой режим при котором амплитуда напряжения или тока на реактивных элементах резко возрарастает по сравнению с входным сигналом.
Условие амплитудного резонанса: Ах(ω0А)→max,
где ω0А –резонансная частота.
Поскольку переходные характеристики резонансных цепей имеют колебательный характер, то резонансные цепи называют колебательными контурами.
Колебательные контуры используются для решения задач частотной избирательности. Под частотной избирательностью понимают способность цепи выделять сигналы узкого диапазона частот.
К простейшим колебательным контурам относят последовательный и параллельный колебательный контур, также систему связанных контуров.

зависит от частоты.

и минимально по сравнению с сопротивлением на других частотах.
2) Начальные

фазы напряжения и тока на контуре одинаковы φu = φi, сдвиг по фазе равен φ = φu – φi = 0.
3) Амплитуда тока в контуре максимальна и равна
4) Сопротивления реактивных элементов L и C одинаковы и равны ρ – характеристическому сопротивлению контура, т.е.

5) Амплитуды напряжений на реактивных элементах контура одинаковы и в Q (добротность) раз больше (амплитуды напряжения на входе).
, Q – добротность контура, .
Поэтому резонанс в последовательном контуре называется резонансом напряжений.
6) Амплитуды напряжений на реактивных элементах находятся в противофазах, а поэтому суммарное напряжение на реактивных элементах равно нулю: .

комплексной амплитуде тока к комплексной амплитуде тока при резонансной частоте,

т.е.

Параметры контура S, Q и ω0 связаны соотношением . Отсюда следует, что чем больше добротность, тем меньше полоса пропускания, тем лучше избирательные свойства колебательного контура.

сопротивления нагрузки (Rн)











Эквивалентная добротность меньше собственной добротности контура Q. Для

того чтобы , необходимо:

Последовательный колебательный контур как четырехполюсник.
На практике используются две схемы включения рис. 5.25.

Подробный анализ показывает, что при высоких добротностях резонансные частоты обеих схем совпадают и равны ω0.

характер, и его модуль имеет максимальное значение по сравнению с

сопротивлением на других частотах.
2. Ток и напряжение совпадают по фазе.
3. Сопротивление реактивных элементов одинаково и равно .
4. Амплитуда тока через реактивные элементы в Q раз превышает ток во внешней цепи. Это вытекает из следующего:


поэтому резонанс в параллельном контуре называется резонансом токов

5) Токи через реактивные элементы сдвинуты по фазе на 180.

;

.

Построим графики АЧХ и ФЧХ входного сопротивления параллельного контура, которые определяются выражениями:
АЧХ: ;

ФЧХ: .
Построенные графики приведены на рис. 5.29.

отношения комплексной амплитуды напряжения на контуре к амплитуде напряжения на

резонансной частоте



.
Вид резонансной характеристики для последовательного и параллельного контуров одинаков, это их и объединяет. По характеру зависимости сопротивления от частоты они обладают противоположными свойствами (см. рис. 5.29).

Схема замещения контура с учетом этих добавочных элементов приведена на

рис. 5.30.











Добротность контура с учетом паразитных элементов называется эквивалентной и определяется выражением






.
Для того чтобы , необходимо:

РИИТ
(кафедра Радиоэлектроники и информационно-измерительной техники)


Электротехника и электроника