Слайд 3Аналитическое решение таких задач, как правило, существует только для достаточно
ограниченного числа подынтегральных функций f(x). В этом случае первообразную можно
представить в виде комбинации алгебраических и трансцендентных функций.
Достаточно часто первообразную F(x) невозможно выразить через элементарные функции. Кроме этого, функция f(x) может задаваться не в виде непрерывной функции, а в виде таблицы ее значений на фиксированном конечном множестве точек. В этом случае понятие первообразной теряет смысл, поэтому для вычисления интеграла применяют численные методы.
Слайд 6Методы интегрирования
Методы Ньютона-Котеса основаны на представлении функции φ(x) в выражении
(1) полиномом различных степеней. К данному классу методов относятся методы
прямоугольников, трапеций, Симпсона.
Методы статистических испытаний (методы Монте-Карло) заключаются в выборе узлов сетки для квадратурного или кубатурного интегрирования на интервале [a, b] с помощью датчика случайных чисел. Конечный результат имеет вероятностный характер. Такие методы, как правило, применяются для вычисления кратных интегралов.
Сплайновые методы основаны на представлении функции φ(x) в выражении (1) кусочным полиномом с условиями связи между отдельными полиномами посредством системы коэффициентов.
Методы наивысшей алгебраической точности заключаются в оптимальной расстановке узлов сетки интегрирования на интервале [a, b] и выборе весовых коэффициентов при замене исходной подынтегральной функции интерполирующей функцией достаточно простого вида. К данному классу методов относятся методы Гаусса-Кристоффеля (вычисление несобственных интегралов), Маркова.
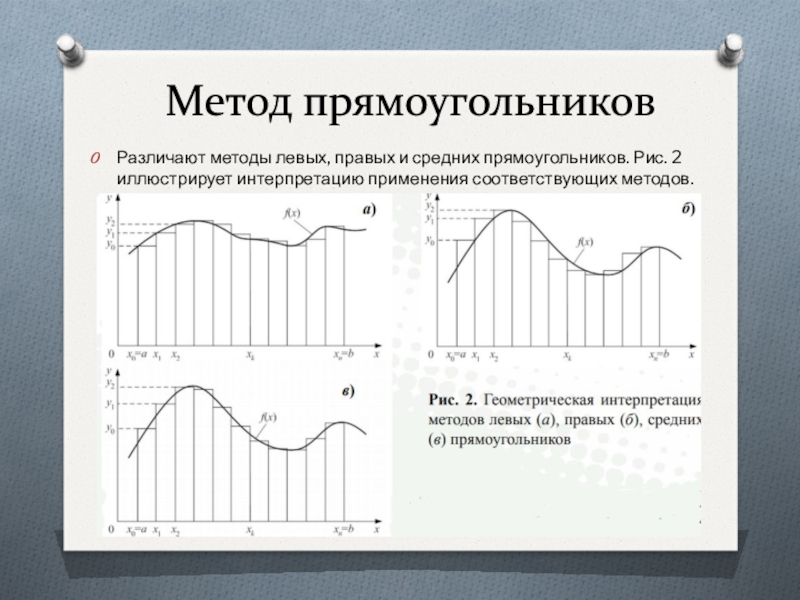
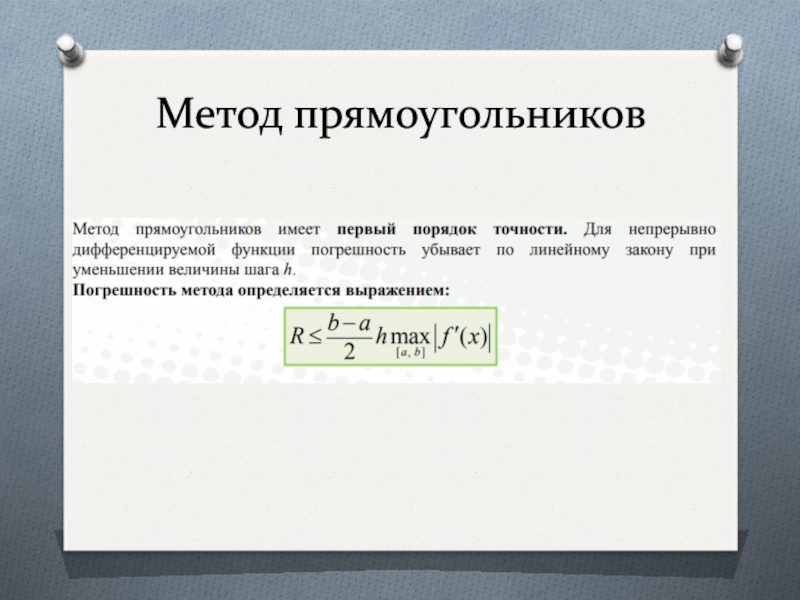
Слайд 7Метод прямоугольников
Различают методы левых, правых и средних прямоугольников. Рис.
2 иллюстрирует интерпретацию применения соответствующих методов.
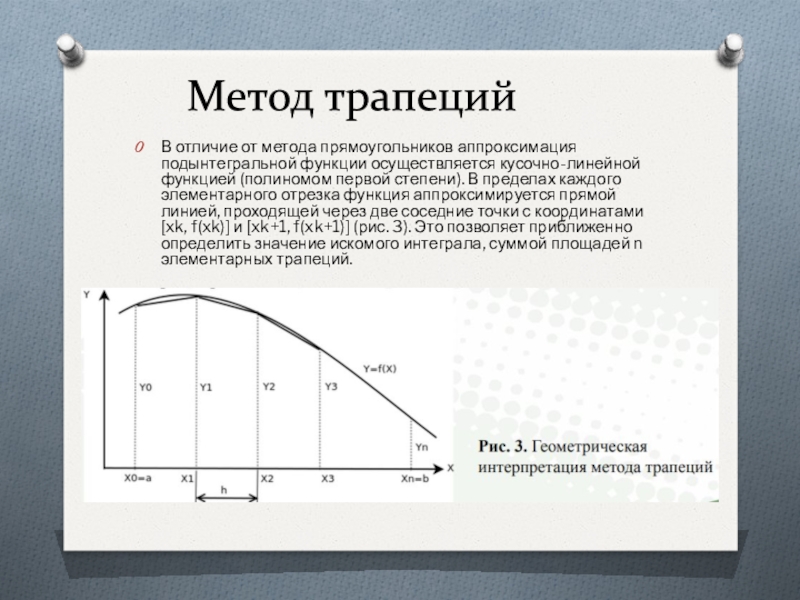
Слайд 11Метод трапеций
В отличие от метода прямоугольников аппроксимация подынтегральной функции
осуществляется кусочно-линейной функцией (полиномом первой степени). В пределах каждого элементарного
отрезка функция аппроксимируется прямой линией, проходящей через две соседние точки с координатами [xk, f(xk)] и [xk+1, f(xk+1)] (рис. 3). Это позволяет приближенно определить значение искомого интеграла, суммой площадей n элементарных трапеций.
Слайд 12Метод трапеций
Выражения для вычисления интеграла в рамках метода трапеций:
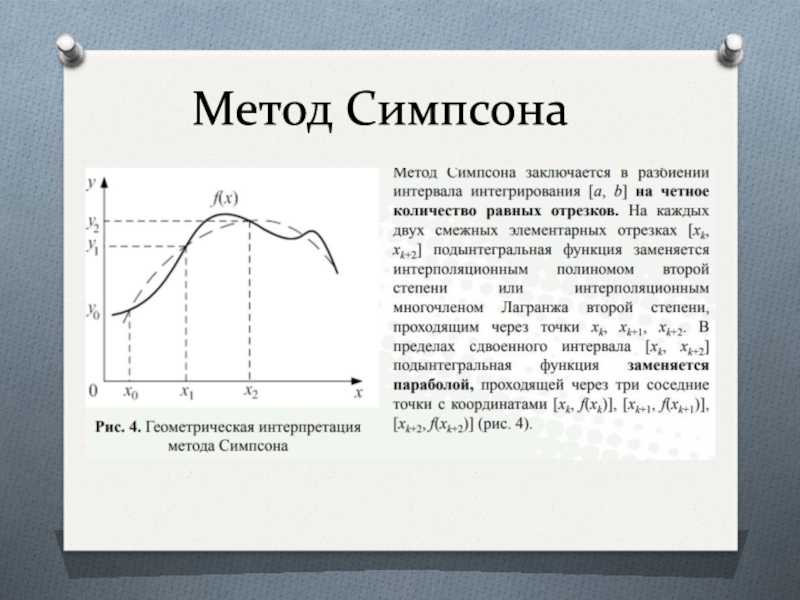
Слайд 14Метод Симпсона
Площадь исходной криволинейной трапеции заменяется суммой n площадей элементарных
криволинейных трапеций:
Слайд 15Примеры решения 15 задач численного интегрирования
Слайд 16Описание наиболее распространенных методов численного интегрирования