Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное интегрирование функции с одной переменной
Содержание
- 1. Численное интегрирование функции с одной переменной
- 2. Постановка задачи численного интегрированияЧисленными методами можно вычислить только определенные интегралыЗаданы пределы интегрирования
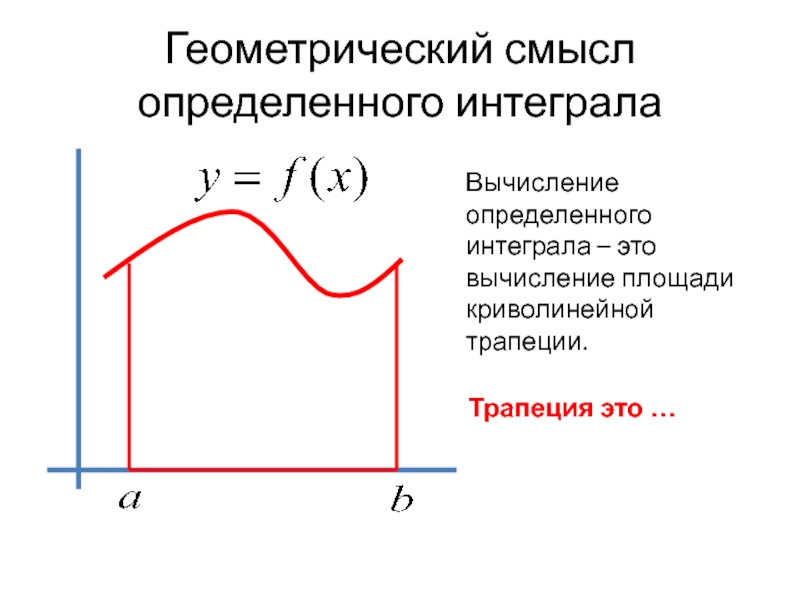
- 3. Геометрический смысл определенного интегралаВычисление определенного интеграла – это вычисление площади криволинейной трапеции.Трапеция это …
- 4. Формула Ньютона-ЛейбницаПервообразная функции f(x)
- 5. Метод прямоугольниковШаг интегрированияn частей одинаковой длины
- 6. Метод прямоугольников=х0 х1 х2 х3a=x0
- 7. Метод левых прямоугольников
- 8. Метод левых прямоугольниковy0y1y2y3y4hhhh
- 9. Метод левых прямоугольников
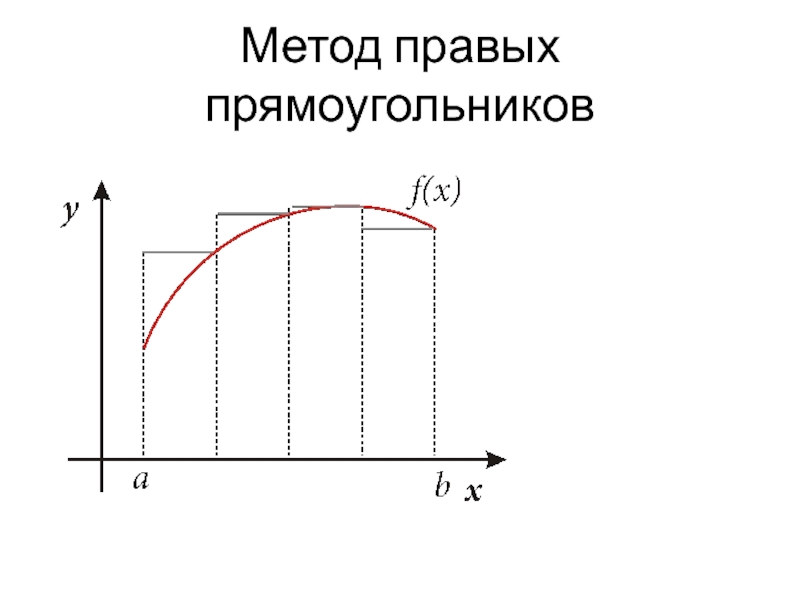
- 10. Метод правых прямоугольников
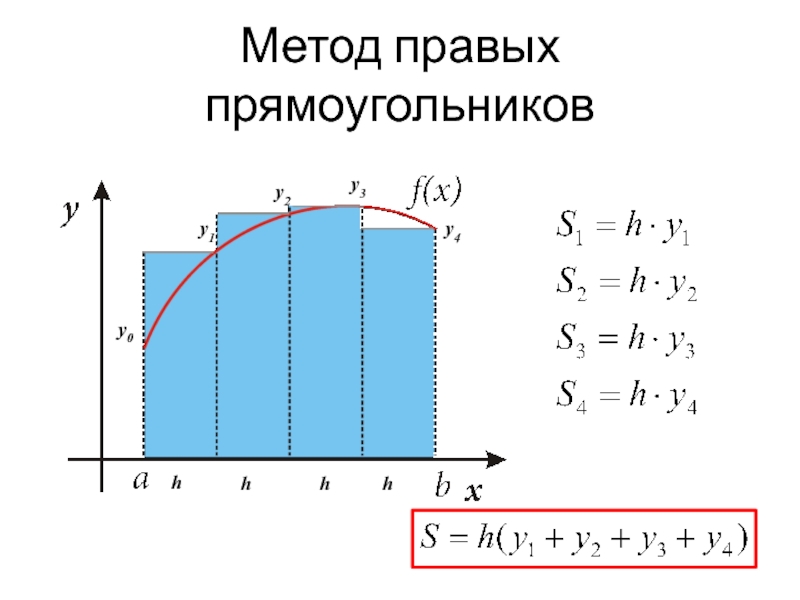
- 11. Метод правых прямоугольниковy0y1y2y3y4hhhh
- 12. Метод правых прямоугольников
- 13. Оценка погрешностиТеорема. Пусть функция f дважды непрерывно
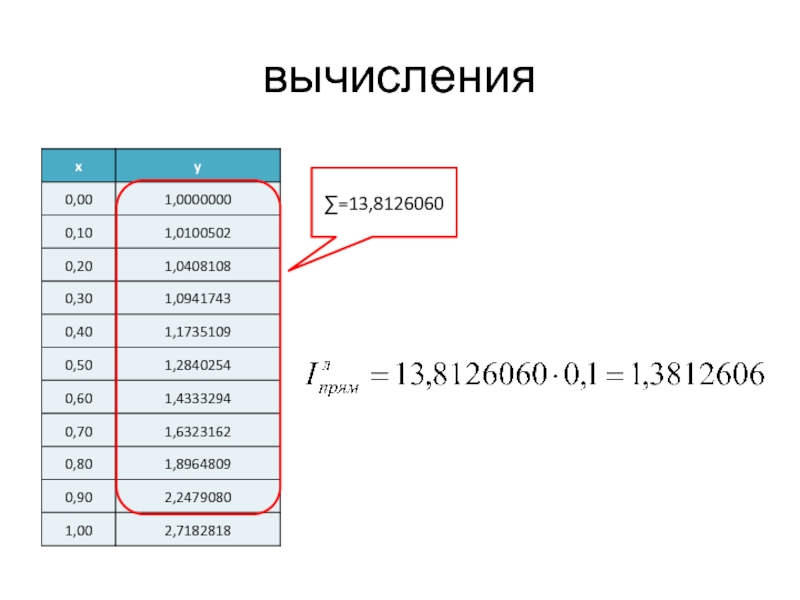
- 14. Пример: вычислить значение интеграла по формуле левых прямоугольников с шагом h=0,1 Составим таблицу значений функции
- 15. вычисления∑=13,8126060
- 16. вычисления
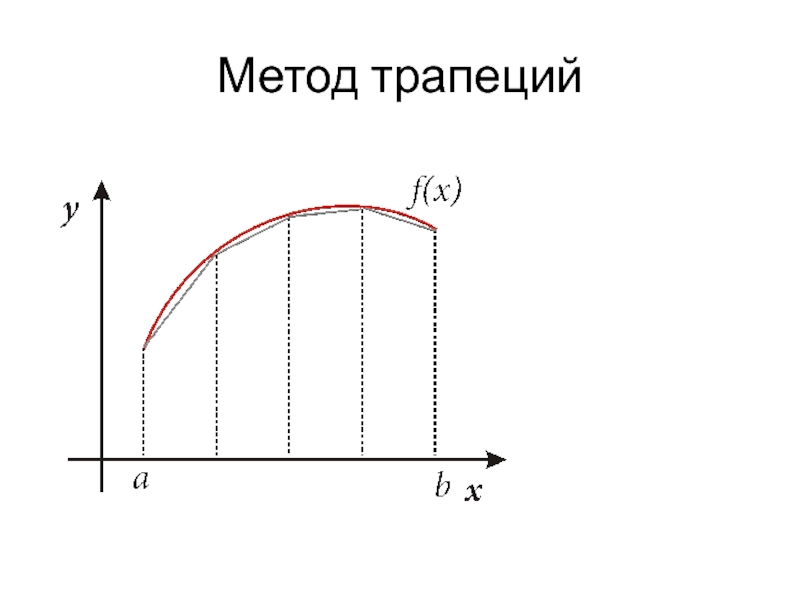
- 17. Метод трапецийТрапеция это…Площадь трапеции…
- 18. Метод трапеций
- 19. Метод трапецийy0y1y2y3y4hhhh
- 20. Метод трапеций
- 21. Оценка погрешностиТеорема. Пусть функция f дважды непрерывно
- 22. Пример:
- 23. Метод Симпсона=х0 х1 х2 х3
- 24. Метод Симпсона
- 25. Метод Симпсона
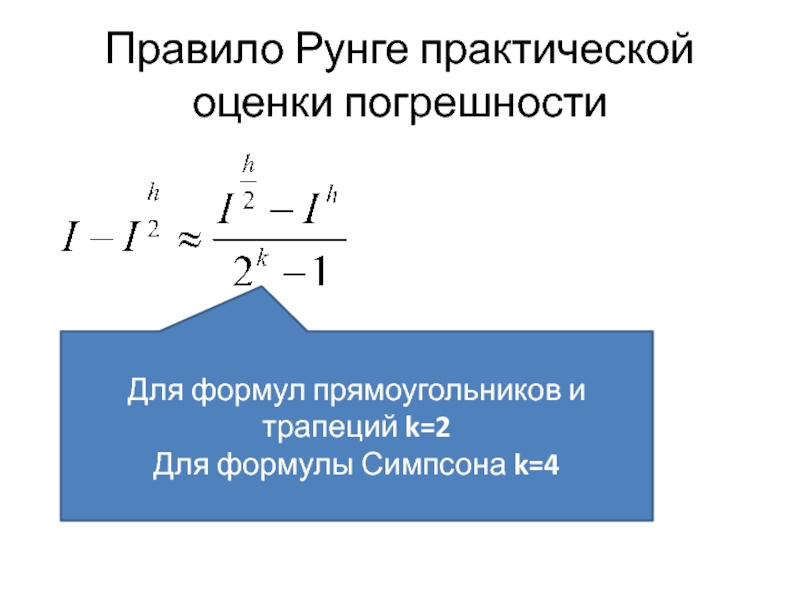
- 26. Правило Рунге практической оценки погрешностиОценки погрешности зависят по hЧем меньше h, тем выше точность
- 27. Правило Рунге практической оценки погрешностиДля формул прямоугольников и трапеций k=2Для формулы Симпсона k=4
- 28. Правило Рунге практической оценки погрешности
- 29. Вычисление интеграла с заданной точностью
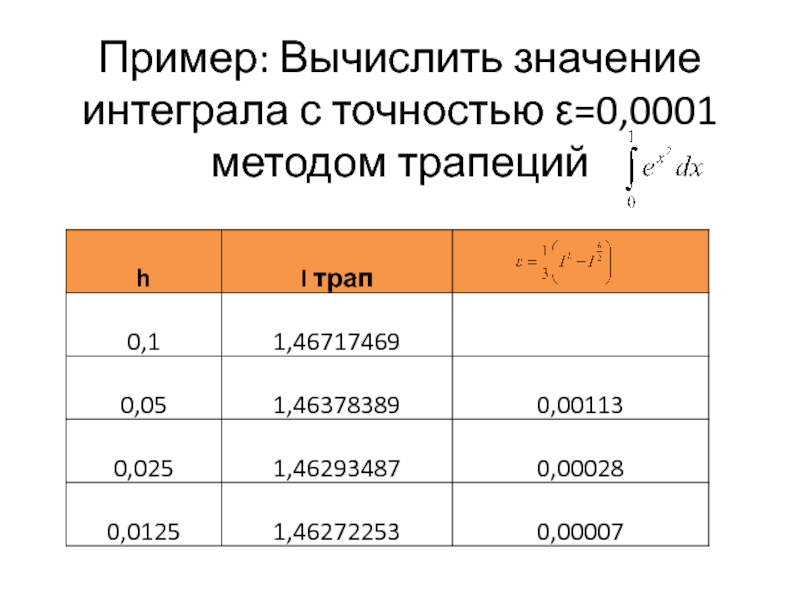
- 30. Пример: Вычислить значение интеграла с точностью ε=0,0001 методом трапеций
- 31. Скачать презентанцию
Постановка задачи численного интегрированияЧисленными методами можно вычислить только определенные интегралыЗаданы пределы интегрирования
Слайды и текст этой презентации
Слайд 2Постановка задачи численного интегрирования
Численными методами можно вычислить только определенные интегралы
Заданы
пределы интегрирования
Слайд 3Геометрический смысл определенного интеграла
Вычисление определенного интеграла – это вычисление площади
криволинейной трапеции.
Трапеция это …
Слайд 13Оценка погрешности
Теорема. Пусть функция f дважды непрерывно дифференцируема на отрезке
[a;b]. Тогда для формулы прямоугольников справедлива следующая оценка погрешности:
где
![Оценка погрешностиТеорема. Пусть функция f дважды непрерывно дифференцируема на отрезке [a;b]. Тогда для формулы прямоугольников справедлива следующая](/img/thumbs/f3cc3730de9b9fb3e69c33334b888c9d-800x.jpg "Численное интегрирование функции с одной переменной Оценка погрешностиТеорема. Пусть функция f дважды непрерывно дифференцируема на отрезке [a;b].")
Слайд 14Пример: вычислить значение интеграла по формуле левых прямоугольников с шагом h=0,1
Составим
таблицу значений функции
Слайд 21Оценка погрешности
Теорема. Пусть функция f дважды непрерывно дифференцируема на отрезке
[a;b]. Тогда для формулы прямоугольников справедлива следующая оценка погрешности:
где
![Оценка погрешностиТеорема. Пусть функция f дважды непрерывно дифференцируема на отрезке [a;b]. Тогда для формулы прямоугольников справедлива следующая](/img/thumbs/7145f6a6f0de8e49794f508e9e6b59a7-800x.jpg "Численное интегрирование функции с одной переменной Оценка погрешностиТеорема. Пусть функция f дважды непрерывно дифференцируема на отрезке [a;b].")
Слайд 26Правило Рунге практической оценки погрешности
Оценки погрешности зависят по h
Чем меньше
h, тем выше точность
Слайд 27Правило Рунге практической оценки погрешности
Для формул прямоугольников и трапеций k=2
Для
формулы Симпсона k=4
