Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное решение СЛАУ с помощью LU- разложения матрицы коэффициентов
Содержание
- 1. Численное решение СЛАУ с помощью LU- разложения матрицы коэффициентов
- 2. Постановка задачи:
- 3. Теорема(об LU-разложении матрицы)Если все главные угловые миноры
- 4. Два вида разложения:1) 2) (3) (4)
- 5. Получение матриц L и U
- 6. Получение расчетных формул для матриц L и U
- 7. Получение расчетных формул для матриц L и U(продолжение)
- 8. Первый шаг второго этапа
- 9. Второй шаг второго этапа
- 10. Вычисление определителя матрицыМетод ГауссаПрямой ходLU-алгоритмили- I вид LU-разложения- II вид LU-разложения
- 11. Обращение матрицы
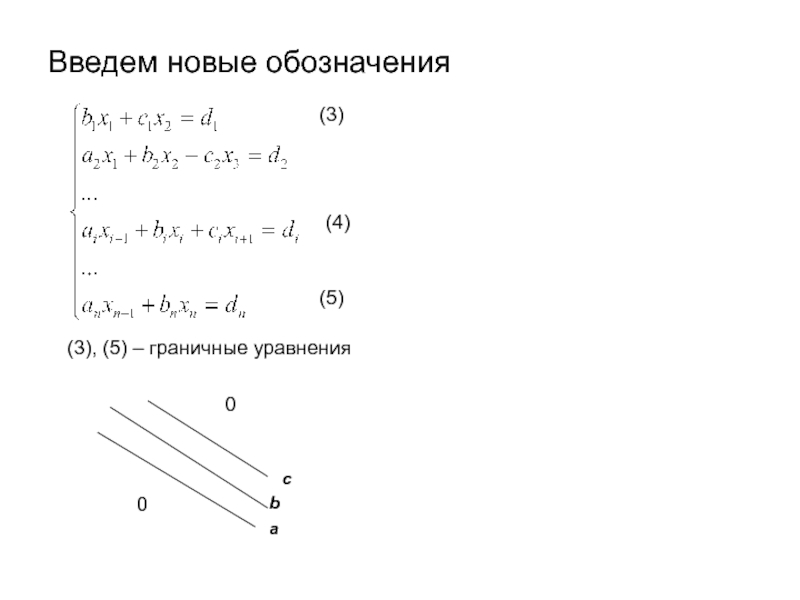
- 12. Введем новые обозначенияПолучим n систем из n уравнений
- 13. Численное решение СЛАУ со специального вида матрицами
- 14. Метод скалярной 3-х точечной прогонкиПостановка задачи:(1) (2)
- 15. Введем новые обозначения(3)
- 16. Зависимость от(6) (6а)
- 17. Вычисление и(7) (8) (9)
- 18. Вычисление и(10) (11) (12)
- 19. Вычисление (13)
- 20. Алгоритм метода скалярной прогонки1. Прогонка вперед –
- 21. Условие применимости методаДостаточным условием применимости метода прогонкиявляется
- 22. Скачать презентанцию
Постановка задачи: (1) (2а)L – нижняя треугольная матрица U – верхняя треугольная матрицаИдея методаLUx = bLy = b ;
Слайды и текст этой презентации
Слайд 1Численное решение СЛАУ с помощью LU-разложения матрицы коэффициентов. Вычисление определителя матрицы. Обращение
матрицы.
Слайд 2Постановка задачи:
(1)
(2а)
L – нижняя треугольная матрица
U – верхняя треугольная матрицаИдея метода
LUx = b
Ly = b ; Ux = y
(2б)
Слайд 3Теорема(об LU-разложении матрицы)
Если все главные угловые миноры матрицы А не
равны нулю, то
матрицу А можно представить в виде
где
L – нижняя треугольная матрица, U – верхняя треугольная матрица. Если какая – либо из матриц L, U имеет ненулевую диагональ, то такое разложение единственно.
Слайд 10Вычисление определителя матрицы
Метод Гаусса
Прямой ход
LU-алгоритм
или
- I вид LU-разложения
- II вид
LU-разложения
Слайд 20Алгоритм метода скалярной прогонки
1. Прогонка вперед – вычисление прогоночных коэффициентов:
Формулы (8), (9).
формула (13);
Формула (6)
2. Прогонка назад – вычисление
Слайд 21Условие применимости метода
Достаточным условием применимости метода прогонки
является требование диагонального преобладания
в матрице А:
(14)
Замечание
Диагональное
преобладание гарантирует что угловые миноры матрицы А отличны от 0(15)