устанавливающего связь между независимой переменной x неизвестной функцией y и
ее производными y’,y”,…,y(n), может мыть представлен следующим образом:Порядок наивысшей производной, входящей в уравнение, называется порядком этого уравнения. Решение дифференциального уравнения (интегрированием) является некоторая функциональная зависимость y=y(x), которая при подстановке в уравнение обращает его в тождество.
Общее решение дифференциального уравнения записывается в виде: y=y(x,c1,c2,…,cn), где c1,c2,…,cn произвольные постоянные.
Решение, полученное из общего решения при фиксированных значениях, называется частным решением уравнения. Постоянные c1,c2,…,cn можно определить, задав n условий. Если эти условия заданы как совокупность значений искомой функции и всех ее производных до (n-1)ого порядка включительно в некоторой течке x0, то задача решения уравнения называется задачей Коши, а заданные условия:
y(x0)=y0, y’(x0)=y’0, y”(x0)=y”0,…, yn-1(x0)=yn-10 называются начальными условиями.
Если условия заданы при разных значениях x, то задача решения дифференциального уравнения называется граничной или краевой задачей.



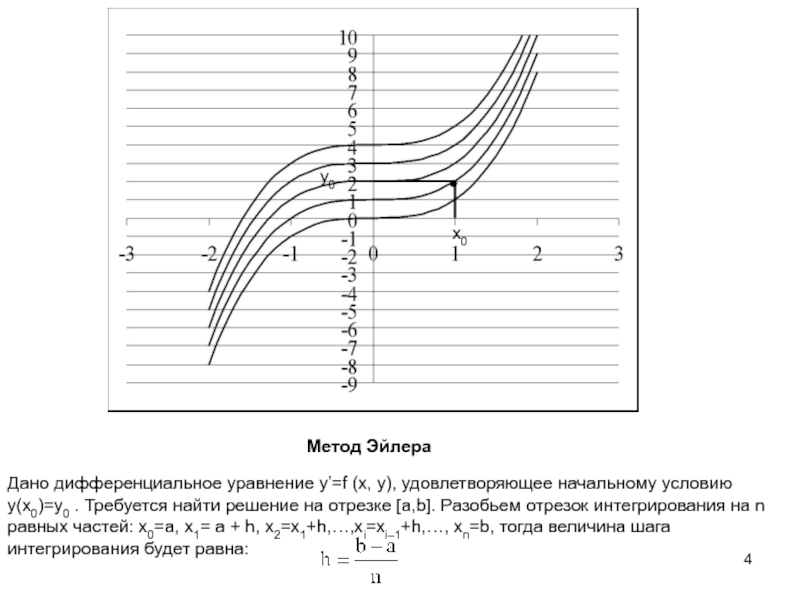
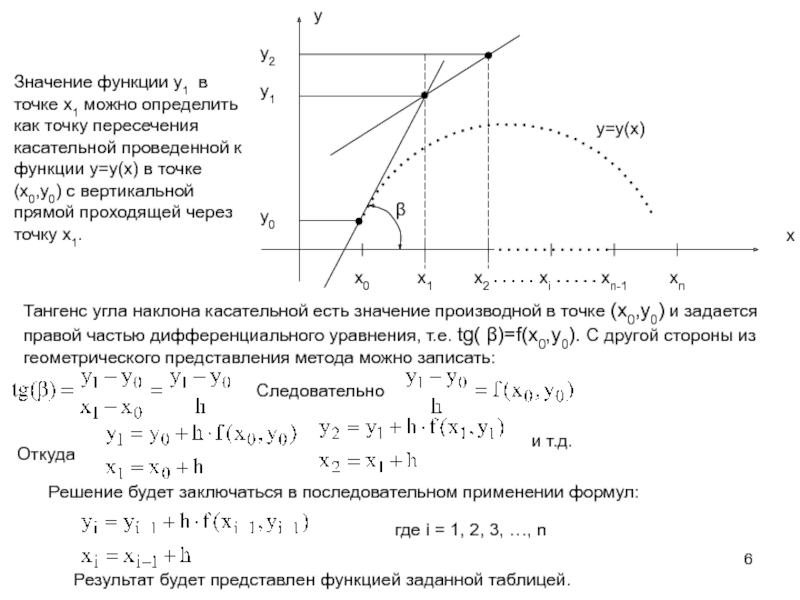
![ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Метод ЭйлераПостановка задачи.Дано дифференциальное уравнение y’=f (x, y), удовлетворяющее начальному условию Метод ЭйлераПостановка задачи.Дано дифференциальное уравнение y’=f (x, y), удовлетворяющее начальному условию y(x0)=y0Требуется найти решение на отрезке [a,b].](/img/thumbs/daae3030b9a8a4bed7c497c9b32848a5-800x.jpg)