Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числовые харрактеристики случайных величин
Содержание
- 1. Числовые харрактеристики случайных величин
- 2. Математическое ожидание д.сл.в.Определение Математическим ожиданием Mξ сл. вел.
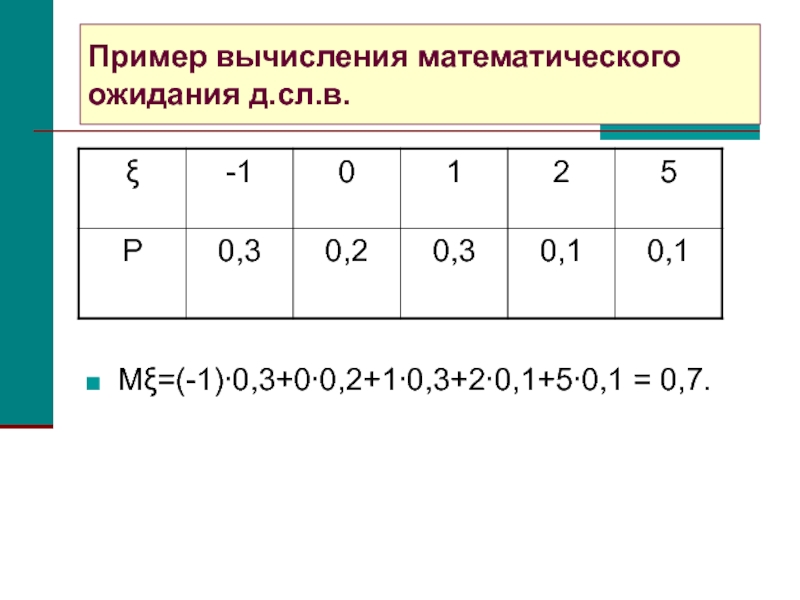
- 3. Пример вычисления математического ожидания д.сл.в.Mξ=(-1)∙0,3+0∙0,2+1∙0,3+2∙0,1+5∙0,1 = 0,7.
- 4. Математическим ожиданием Mξ сл. в. ξ
- 5. ЗамечаниеЕсли то говорят, что математическое ожидание не существует.
- 6. Математическое ожидание функции дискретной случайной величиныМатематическим
- 7. Математическое ожидание функции непрерывной случайной величины
- 8. Свойства матожидания1. MC = C, (С =
- 9. Дисперсия случайной величиныОпределение.Если случайная величина ξ имеет
- 10. Свойства дисперсииДисперсия любой случайной величины неотрицательна, Dξ
- 11. Свойства дисперсииЕще одно важное свойство дисперсии
- 12. Вычисление дисперсииДля вычисления дисперсии надо найти Mξ2
- 13. Вычисление Mξ2
- 14. Пример вычисления дисперсииMξ2=(-1)2∙0,3+02∙0,2+12∙0,3+22∙0,1+52∙0,1 = 3,5.Mξ = 0,7.Dξ = 3,5 – (0,7)2 = 3,01.
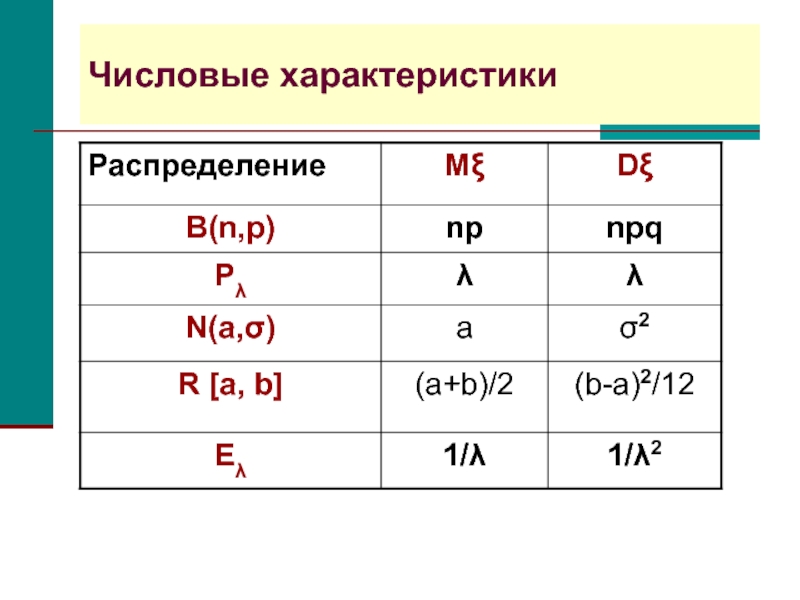
- 15. Числовые характеристики
- 16. Пример
- 17. Начальные и центральные моменты Определение. Начальным моментом
- 18. Среднеквадратичное отклонениеДля определения меры разброса значений случайной
- 19. Замечания1. Математическое ожидание случайной величины - начальный
- 20. Коэффициент асимметрии Определение. Коэффициентом асимметрии называется
- 21. ЗамечанияУ симметричного распределения асимметрия равна 0. Асимметрия
- 22. Пример: A < 0
- 23. Пример: A > 0
- 24. Коэффициент эксцесса Определение. Коэффициентом эксцесса называется число Е, которое определяется формулой
- 25. ЗамечанияКоэффициент эксцесса указывает на«островершинность» или «плосковершинность» графика
- 26. Пример: E > 0
- 27. Мода Определение. Модой непрерывной случайной величины ξ
- 28. ПримерМода m0 дискретной случайной величины ξ равна
- 29. Медиана Определение. Медианой непрерывной случайной величины ξ
- 30. Чтобы найти медиану, надо решить уравнениеКорень этого уравнения и есть медиана.(Если корней несколько, выберите правильный).
- 31. Пример. Найти медиану показательного р-я E4
- 32. Пример: мода, медиана и Mξm0 = 8; me = 9,34; Mξ = 10.
- 33. Квантиль порядка q Определение. Квантилью порядка q, 0 < q
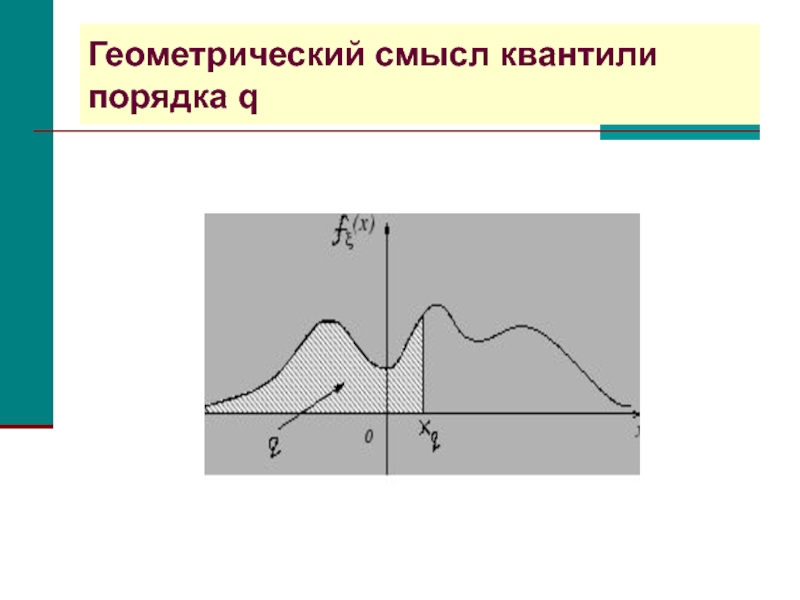
- 34. Геометрический смысл квантили порядка q
- 35. Чтобы найти квантиль xq, надо решить уравнениеКорень
- 36. Пример. Найти квантиль x0,3 в R[2,5]. Fξ(xq) = q.
- 37. Скачать презентанцию
Математическое ожидание д.сл.в.Определение Математическим ожиданием Mξ сл. вел. ξ с дискретным распределением, задаваемым законом распределения P(ξ=xi) = pi, называется число Смысл: Математическое ожидание – это среднее значение случайной величины.
Слайды и текст этой презентации
Слайд 1Теория вероятностей и математическая статистика
Числовые характеристики
случайных величин
ЛЕКЦИЯ 6
Слайд 2Математическое ожидание д.сл.в.
Определение
Математическим ожиданием Mξ сл. вел. ξ с дискретным
распределением, задаваемым законом распределения P(ξ=xi) = pi, называется число
Математическое ожидание – это среднее значение случайной величины.
Слайд 4
Математическим ожиданием Mξ сл. в. ξ с абсолютно
непрерывным распределением с плотностью распределения fξ(x) называется число
Математическое
ожидание н.сл.в.
Слайд 6Математическое ожидание функции
дискретной случайной величины
Математическим ожиданием функции φ(ξ) дискретной
случайной величины ξ, имеющей распределение P(ξ =xi) = pi, называется
величина M[φ(ξ)], равная
Слайд 7Математическое ожидание функции
непрерывной случайной величины
Математическое ожидание функции непрерывной
случайной величины с плотностью вероятностей fξ (x)
вычисляется по формуле
Слайд 8Свойства матожидания
1. MC = C, (С = const )
2. M(Cξ)
= C∙Mξ,
3. M(ξ + η ) = M ξ +
M η ,4. M(ξ ∙ η) = M ξ ∙Mη (для независимых величин).
Слайд 9Дисперсия случайной величины
Определение.
Если случайная величина ξ имеет математическое ожидание M
ξ , то дисперсией случайной величины ξ называется величина
D ξ = M(ξ - M ξ )2. Смысл: Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.
Слайд 10Свойства дисперсии
Дисперсия любой случайной величины неотрицательна, Dξ ≥ 0;
Дисперсия
константы равна нулю, Dc = 0;
Для произвольной константы
D(cξ ) = c2D(ξ );Дисперсия суммы или разности
независимых случайных величин равна сумме их дисперсий:
D(ξ ± η) = D(ξ) + D(η).
Слайд 12Вычисление дисперсии
Для вычисления дисперсии надо найти Mξ2 и отнять квадрат
математического ожидания,
Dξ = Mξ2 - (Mξ)2.
Величина Mξ2 для
дискретных и непрерывных случайных величин соответственно вычисляется по формулам 
Слайд 14Пример вычисления дисперсии
Mξ2=(-1)2∙0,3+02∙0,2+12∙0,3+22∙0,1+52∙0,1 = 3,5.
Mξ = 0,7.
Dξ = 3,5 –
(0,7)2 = 3,01.
Слайд 17Начальные и центральные моменты
Определение. Начальным моментом k-го порядка случайной
величины ξ называется математическое ожидание k-й степени случайной величины ξ
, т.е. αk = Mξ k.Определение. Центральным моментом k-го порядка случайной величины ξ называется величина μk, определяемая формулой
μk = M(ξ - Mξ )k.
Слайд 18Среднеквадратичное отклонение
Для определения меры разброса значений случайной величины часто используется
среднеквадратичное отклонение σξ, связанное с дисперсией соотношением σξ = √Dξ.
Смысл
среднеквадратичного отклонения: линейная мера разброса. 
Слайд 19Замечания
1. Математическое ожидание случайной величины - начальный момент первого порядка,
α1 = Mξ1.
2. Дисперсия - центральный момент
второго порядка, μ 2 = M(ξ - M ξ )2 = Dξ .3. Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:
μ 2 = α2 - (α1)2 .
Слайд 20Коэффициент асимметрии
Определение. Коэффициентом асимметрии называется число A, которое
определяется формулой
где μ3 - центральный момент третьего порядка,
σ
- среднеквадратичное отклонение.
Слайд 21Замечания
У симметричного распределения асимметрия равна 0.
Асимметрия распределения с длинным
правым хвостом положительна.
Если распределение имеет длинный левый хвост, то
его асимметрия отрицательна. 
Слайд 24Коэффициент эксцесса
Определение. Коэффициентом эксцесса называется число Е, которое
определяется формулой
Слайд 25Замечания
Коэффициент эксцесса указывает на
«островершинность» или «плосковершинность» графика плотности.
Если Е
> 0, то это означает, что график плотности вероятностей сильнее
“заострен”, чем у нормального распределения, если же Е < 0, то “заостренность” графика меньше, чем у нормального распределения.У нормального распределения А = 0 и Е = 0.
Слайд 27Мода
Определение. Модой непрерывной случайной величины ξ называется значение m0,
при котором плотность fξ(x) достигает максимума.
Модой дискретной случайной величины
ξ называется значение m0, при которомp(ξ = m0 )= max pi
Слайд 28Пример
Мода m0 дискретной случайной величины
ξ равна значению ξ =
1, т.к. p(ξ = 1)= max pi.
m0 = 1.
Слайд 29Медиана
Определение. Медианой непрерывной случайной величины ξ называется значение me,
при котором F(me) = 1/2.
Замечание. Для непрерывной случайной величины
ξ это определение равносильно следующему:
Слайд 30Чтобы найти медиану, надо решить уравнение
Корень этого уравнения и есть
медиана.
(Если корней несколько, выберите правильный).
Слайд 33Квантиль порядка q
Определение. Квантилью порядка q, 0 < q
= q.
Смысл. Квантиль порядка q отсекает слева 100∙q% значений случайной величины.
Замечание. Медиана – это квантиль порядка 0,5.
Смысл. Квантиль порядка q отсекает слева 100∙q% значений случайной величины.
Замечание. Медиана – это квантиль порядка 0,5.
Слайд 35Чтобы найти квантиль xq, надо решить уравнение
Корень этого уравнения и
есть квантиль порядка q.
(Если корней несколько, выберите правильный).
![Пример. Найти квантиль x0,3 в R[2,5]. Fξ(xq) = q.](/img/thumbs/dc78c50e77433d259f29aa56e7bd4efa-800x.jpg "Числовые харрактеристики случайных величин Пример. Найти квантиль x0,3 в R[2,5]. Fξ(xq) = q.")
