Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
циклические коды
Содержание
- 1. циклические коды
- 2. Понятие циклического кодаЦиклический код относится к линейным,
- 3. Преимущества циклических кодовЭффективность при обнаружении и исправлении
- 4. Создание циклического кода Идея построения циклических кодов базируется
- 5. 2 способа получения кодовой комбинацииКодовая комбинация циклического
- 6. Основное свойство циклического кода Название циклических кодов связаны
- 7. Пример получения кодовой комбинации:Дано: Р(х)=х*3+х+1, передаваемая комбинация
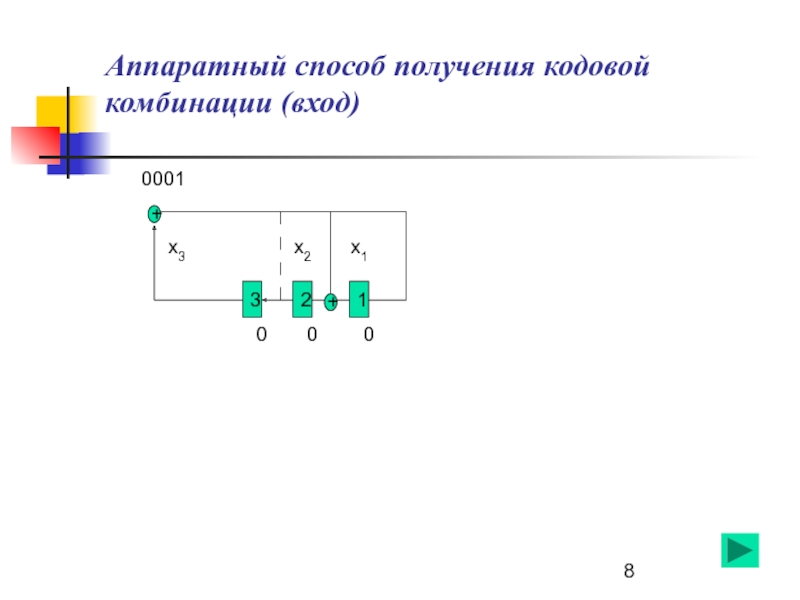
- 8. +1+230001000x3x2x1Аппаратный способ получения кодовой комбинации (вход)
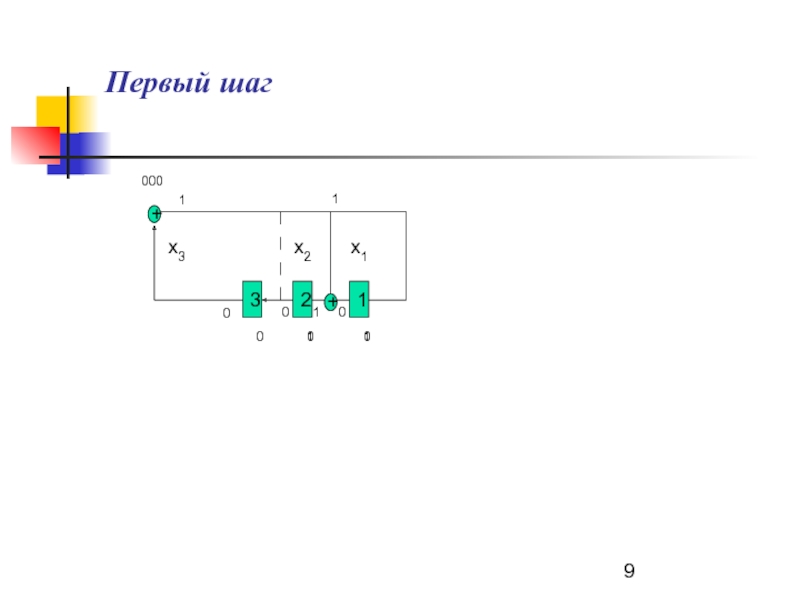
- 9. +1+23000000x3x2x110110101Первый шаг
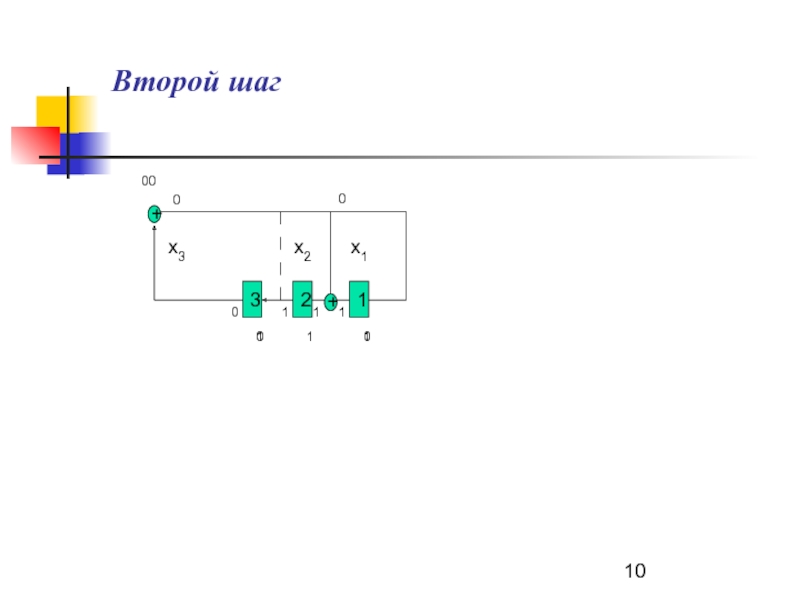
- 10. +1+2300011x3x2x100010111Второй шаг
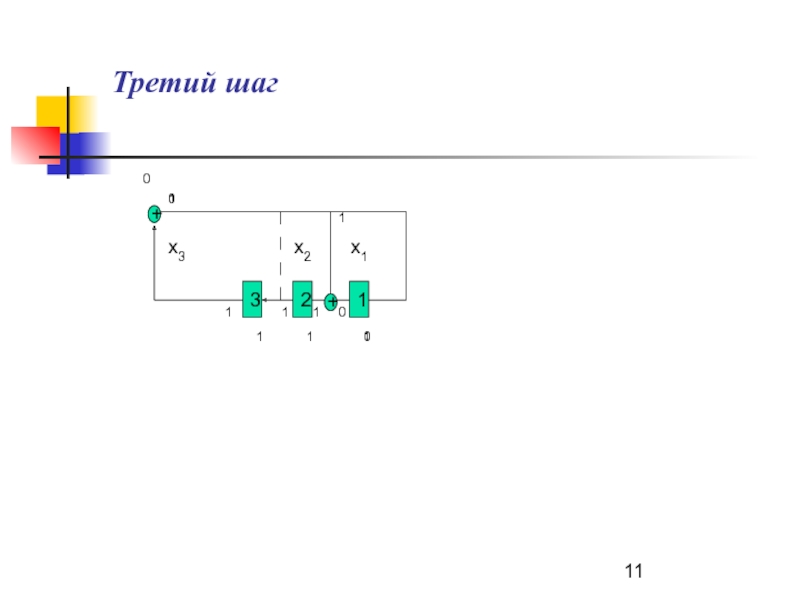
- 11. +1+230110x3x2x101110111Третий шаг
- 12. +1+230111x3x2x11111001Заключительный шагЕдиница в 3 и 1 ячейке, что соответствует х*2+1;Остаток совпадает с рассчитанным ранее.
- 13. Декодирующее устройство17+Деление на P(х)ДешифраторНа входе F(х)Если деление
- 14. Пример работы декодирующего устройства7654321Деление на P(х)ОстатокИЛИПравильная комбинация: 100010111000010
- 15. Пример работы декодирующего устройства7654321Деление на P(х)ОстатокИЛИНеправильная комбинация: 1000111111000110000
- 16. Заключение В данной презентации был рассмотрен один из
- 17. Спасибо за внимание! Удачного дня и творческих успехов! С уважением, Максимова Евгения.27.04.2007
- 18. Скачать презентанцию
Понятие циклического кодаЦиклический код относится к линейным, блочным, корректирующим, равномерным кодам;Кодовые комбинации представляются в виде многочленов, что позволяет свести действия над кодовыми комбинациями к действием над многочленами (используя аппарат полиномиальной алгебры);Включают
Слайды и текст этой презентации
Слайд 1Курсовая работа по предмету: «Сети ЭВМ и телекоммуникации» тема презентации: «Циклические
коды»
Слайд 2Понятие циклического кода
Циклический код относится к линейным, блочным, корректирующим, равномерным
кодам;
Кодовые комбинации представляются в виде многочленов, что позволяет свести действия
над кодовыми комбинациями к действием над многочленами (используя аппарат полиномиальной алгебры);Включают в себя в качестве одной из разновидностей коды Хэмминга;
Первоначально были созданы для упрощения схем кодирования и декодирования;
Слайд 3Преимущества циклических кодов
Эффективность при обнаружении и исправлении ошибок;
Гибкость с точки
зрения возможности реализации кодов с необходимой способностью обнаружения;
Простота реализации соответствующих
кодеров и декодеров;Все операции с кодом легко реализуются аппаратно на регистрах сдвига с обратными связям;
Слайд 4Создание циклического кода
Идея построения циклических кодов базируется на использовании неприводимых
многочленов. Неприводимым называется многочлен, который не может быть представлен в
виде произведения многочленов низших степеней ,т.е. такой многочлен делиться только на самого себя или на единицу и не делиться ни на какой другой многочлен. На такой многочлен делиться без остатка двучлен x*n+1. Неприводимые многочлены в теории циклических кодов играют роль образующих полиномов;* n- в степени n;
Слайд 52 способа получения кодовой комбинации
Кодовая комбинация циклического n-значного кода может
быть получена следующими двумя способами:
1) умножение кодовой комбинации Q(x)
простого кода на одночлен x*r и добавление к этому произведению остатка R(x) , полученного в результате
деления произведения Q(x) x*r на образующий полином P(x);
2) умножения кодовой комбинации C(x) простого k-значного на образующий полином P(x).
При построении циклических кодов первым способом расположение информационных символов во всех комбинациях строго упорядочено -
они занимают k старших разрядов комбинации, а остальные (n-k) разрядов
отводятся под контрольные.
При втором способе образования циклических кодов информационные и контрольные символы в комбинациях циклического кода не отделены друг от друга, что затрудняет процесс декодирования.
Слайд 6Основное свойство циклического кода
Название циклических кодов связаны с тем, что
все разрешенные комбинации бит в передаваемом сообщении (кодовые слова) могут
быть получены путем операции циклического сдвига некоторого исходного кодового слова;Сдвиг справа налево осуществляется путем умножения полинома на x ;
Создание разрешенных комбинаций:
1
1
0
1
Слайд 7Пример получения кодовой комбинации:
Дано: Р(х)=х*3+х+1, передаваемая комбинация 1000;
Решение: а) умножение
на Р(х);
G(х)=х*3, т.к. в комбинации только х*3=1;
F(х)=P(х)G(х)=(х*3+х+1)х*3=х*6+х*4+х*3;
R(х)=0; комбинация разрешенная;
б) деление
на P(х);т.к. х*3, r=3. G(х)х*r=х*6;
делим G(х)х*r на Р(х), R(х)=х*2+1;
F(х)=G(х)х*r+R(х); F(х)=х*6+х*2+1;
При делении F(х) на Р(х) R(х)=0; комбинация разрешенная;
Слайд 12+
1
+
2
3
0
1
1
1
x3
x2
x1
1
1
1
1
0
0
1
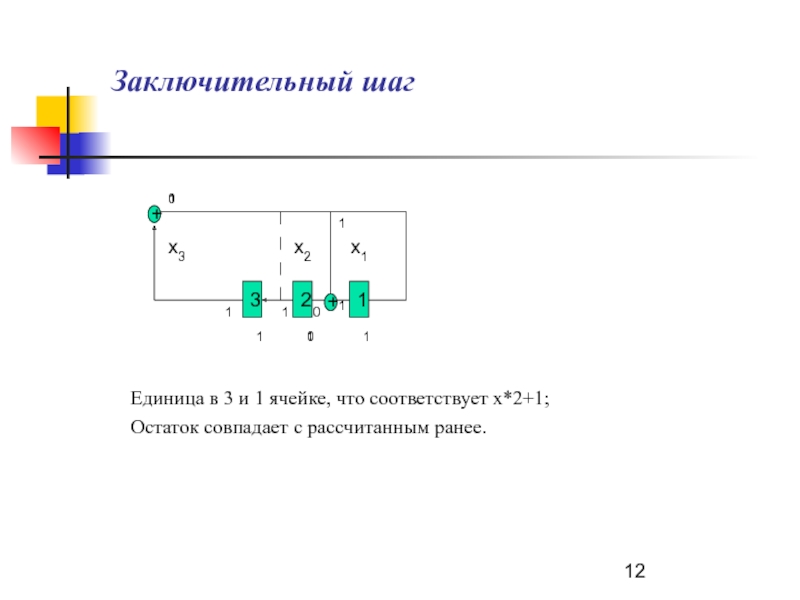
Заключительный шаг
Единица в 3 и 1 ячейке, что соответствует х*2+1;
Остаток
совпадает с рассчитанным ранее.
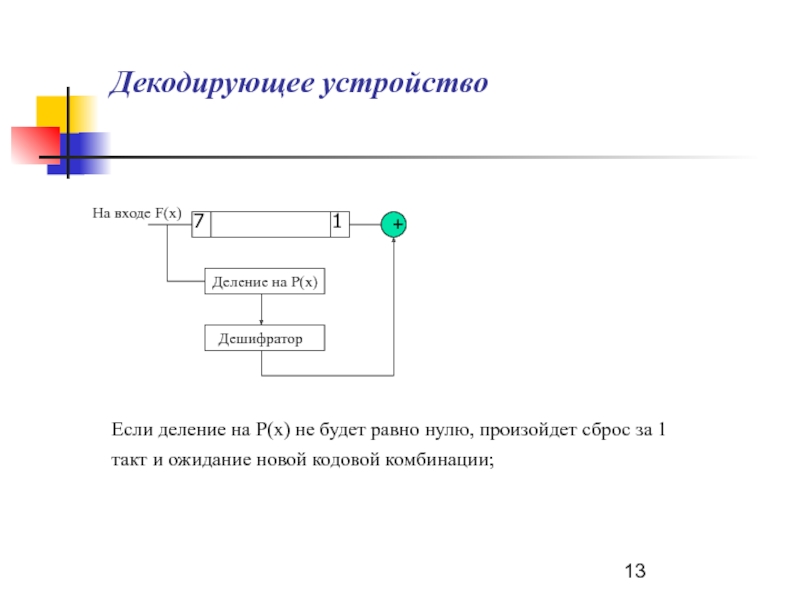
Слайд 13Декодирующее устройство
1
7
+
Деление на P(х)
Дешифратор
На входе F(х)
Если деление на P(х) не
будет равно нулю, произойдет сброс за 1 такт и ожидание
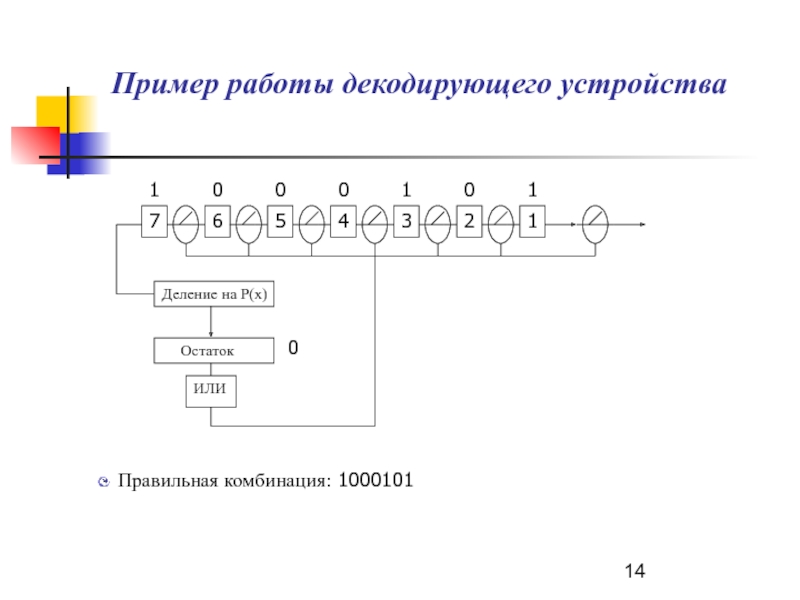
новой кодовой комбинации;Слайд 14Пример работы декодирующего устройства
7
6
5
4
3
2
1
Деление на P(х)
Остаток
ИЛИ
Правильная комбинация: 1000101
1
1
0
0
0
0
1
0
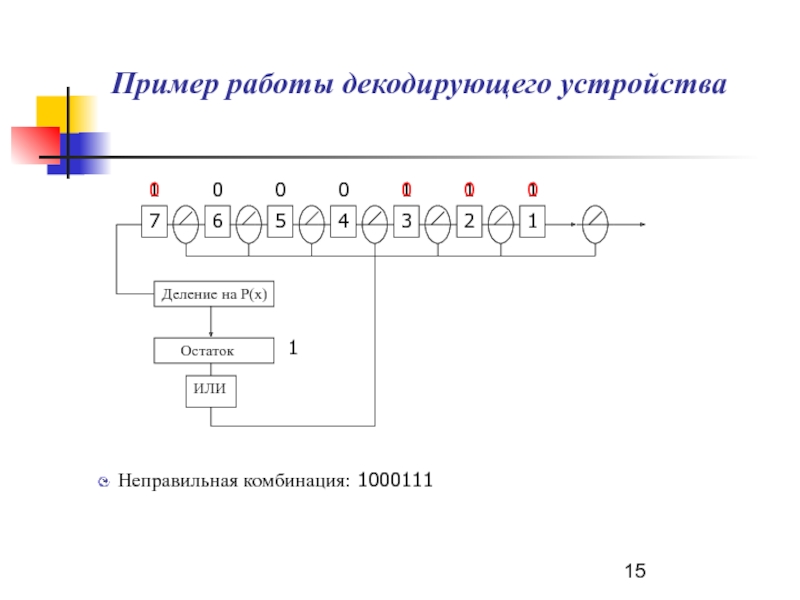
Слайд 15Пример работы декодирующего устройства
7
6
5
4
3
2
1
Деление на P(х)
Остаток
ИЛИ
Неправильная комбинация: 1000111
1
1
1
0
0
0
1
1
0
0
0
0
Слайд 16Заключение
В данной презентации был рассмотрен один из самых простых и
эффективных кодов, способный кодировать, обнаруживать и исправлять ошибки передачи информации.
Из-за простоты схемной и программной реализации циклические коды получили широкое распространение и признание.