Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
CONTROL AUTOMATICO
Содержание
- 1. CONTROL AUTOMATICO
- 2. MODELOS MATEMATICOS DE LOS SISTEMASRepresentación gráfica de
- 3. MODELOS MATEMATICOS DE LOS SISTEMASRepresentación gráfica de
- 4. MODELOS MATEMATICOS DE LOS SISTEMASRepresentación gráfica de
- 5. MODELOS MATEMATICOS DE LOS SISTEMASRepresentación gráfica de
- 6. MODELOS MATEMATICOS DE LOS SISTEMASRepresentación gráfica de
- 7. MODELOS MATEMATICOS DE LOS SISTEMASRepresentación gráfica de
- 8. MODELOS MATEMATICOS DE LOS SISTEMASComportamiento DinámicoDiagrama Funcional Ecuación diferencial del sistema
- 9. MODELOS MATEMATICOS DE LOS SISTEMASModelo del sistema
- 10. MODELOS MATEMATICOS DE LOS SISTEMASAproximación lineal de un sistema físico en estado estacionario.
- 11. MODELOS MATEMATICOS DE LOS SISTEMASAproximación lineal de
- 12. MODELOS MATEMATICOS DE LOS SISTEMASAproximación lineal de
- 13. MODELOS MATEMATICOS DE LOS SISTEMASAproximación lineal de
- 14. Comportamiento Estático de un SistemaComportamiento estático de
- 15. Comportamiento Estático de un SistemaComportamiento estático de
- 16. MODELOS MATEMATICOS DE LOS SISTEMASComportamiento estático de
- 17. MODELOS MATEMATICOS DE LOS SISTEMASComportamiento estático de
- 18. MODELOS MATEMATICOS DE LOS SISTEMASComportamiento dinámico de un generador de corriente continua
- 19. MODELOS MATEMATICOS DE LOS SISTEMAS
- 20. Función de Transferencia de un SistemaUn sistema
- 21. MODELOS MATEMATICOS DE LOS SISTEMASFunción de Transferencia
- 22. MODELOS MATEMATICOS DE LOS SISTEMASFunción de Transferencia de un SistemaTransformadainversade Laplace“Multiplicación”“Convolución”
- 23. Aproximación lineal de un sistema físicoLa gran
- 24. MODELOS MATEMATICOS DE LOS SISTEMASMotor de Corriente
- 25. MODELOS MATEMATICOS DE LOS SISTEMASMotor de Corriente
- 26. MODELOS MATEMATICOS DE LOS SISTEMASMotor de Corriente Continua
- 27. MODELOS MATEMATICOS DE LOS SISTEMASMotor de Corriente
- 28. MODELOS MATEMATICOS DE LOS SISTEMASMotor de Corriente Continua controlado por CampoL
- 29. MODELOS MATEMATICOS DE LOS SISTEMASMotor de Corriente Continua controlado por CampoIa constanteFunción de transferencia
- 30. MODELOS MATEMATICOS DE LOS SISTEMASMotor de Corriente Continua controlado por ArmaduraL
- 31. MODELOS MATEMATICOS DE LOS SISTEMASMotor de Corriente Continua controlado por ArmaduraIf constanteFunción de transferencia
- 32. Amplificador Rotativo de dos Etapas, AmplidinaNOTA: El
- 33. MODELOS MATEMATICOS DE LOS SISTEMASRegulador Hidráulico, servomotor
- 34. MODELOS MATEMATICOS DE LOS SISTEMASRegulador Hidráulico, servomotor hidráulicoA Superficie del pistón deLa Función de Transferencia:L
- 35. MODELOS MATEMATICOS DE LOS SISTEMASRegulador Hidráulico, servomotor
- 36. MODELOS MATEMATICOS DE LOS SISTEMASSistema de engranajesSistema
- 37. Sistema de engranajesSe incluye la fricción viscosa
- 38. MODELOS MATEMATICOS DE LOS SISTEMASSistema HidráulicoSistema ideal,
- 39. Detector de Error utilizando PotenciómetrosPotenciómetros de 360o, sin topeMODELOS MATEMATICOS DE LOS SISTEMAS
- 40. Tacómetro (tacogenerador)MODELOS MATEMATICOS DE LOS SISTEMAS
- 41. MODELOS MATEMATICOS DE LOS SISTEMASSistema TérmicoLa variación
- 42. MODELOS MATEMATICOS DE LOS SISTEMASSistema TérmicoBalance Energético
- 43. MODELOS MATEMATICOS DE LOS SISTEMASControl de VelocidadMotor
- 44. MODELOS MATEMATICOS DE LOS SISTEMASControl de VelocidadMotor de Corriente Continua controlado por armadura
- 45. MODELOS MATEMATICOS DE LOS SISTEMASControl de PosiciónMotor
- 46. MODELOS MATEMATICOS DE LOS SISTEMASControl de PosiciónMotor
- 47. MODELOS MATEMATICOS DE LOS SISTEMASControl de PosiciónMotor de Corriente Continua controlado por armadura
- 48. Modelos de diagramas de bloquesLos diagramas de
- 49. MODELOS MATEMATICOS DE LOS SISTEMASModelos de diagramas
- 50. MODELOS MATEMATICOS DE LOS SISTEMASModelos de diagramas
- 51. MODELOS MATEMATICOS DE LOS SISTEMASModelos de diagramas
- 52. Gráficos de Flujo de SeñalUna gráfica de
- 53. MODELOS MATEMATICOS DE LOS SISTEMASGráficos de Flujo
- 54. MODELOS MATEMATICOS DE LOS SISTEMASGráficos de Flujo
- 55. MODELOS MATEMATICOS DE LOS SISTEMASGráfico de Flujo
- 56. MODELOS MATEMATICOS DE LOS SISTEMASGráfico de Flujo
- 57. Resolución de Gráficos de Flujo de Señales
- 58. MODELOS MATEMATICOS DE LOS SISTEMASResolución de Gráficos
- 59. MODELOS MATEMATICOS DE LOS SISTEMASResolución de Gráficos
- 60. MODELOS MATEMATICOS DE LOS SISTEMASResolución de Gráficos
- 61. Resolución de Gráficos de Flujo de Señales
- 62. MODELOS MATEMATICOS DE LOS SISTEMASResolución de Gráficos
- 63. Comandos de MATLABGeneración de una función de
- 64. MODELOS MATEMATICOS DE LOS SISTEMASComandos de MATLABObtención
- 65. MODELOS MATEMATICOS DE LOS SISTEMASComandos de MATLABCascada
- 66. MODELOS MATEMATICOS DE LOS SISTEMASComandos de MATLABCascada
- 67. Comandos de MATLABSimplificación de Diagramas de BloquesAplicar
- 68. MODELOS MATEMATICOS DE LOS SISTEMASComandos de MATLABSimplificación
- 69. MODELOS MATEMATICOS DE LOS SISTEMASComandos de MATLABSimplificación
- 70. MODELOS MATEMATICOS DE LOS SISTEMASComandos de MATLABSimplificación
- 71. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2MODELOS MATEMATICOS DE LOS SISTEMAS
Representación gráfica de un sistema en
el dominio del tiempo
Diagramas Funcionales
Señales
Bifurcación de Señales
Punto de sumas de
SeñalesInversión de Polaridad
Bloques de Transferencia
Слайд 3MODELOS MATEMATICOS DE LOS SISTEMAS
Representación gráfica de un sistema en
el dominio del tiempo
Diagrama Funcional
Control de velocidad de un auto.
Fuerza
debido al viento es proporcional a la velocidad: fLFuerza debido a fricción de las llantas es proporcional a la velocidad: fR
Fuerza debido al peso en dirección del movimiento, es proporcional a la pendiente: fG
Fuerza de Empuje: fA
Fuerza Resultante: fres
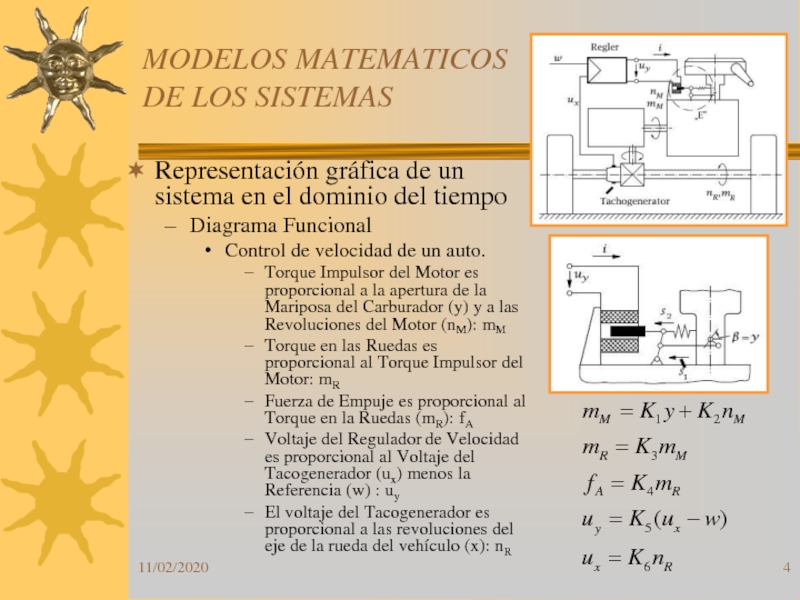
Слайд 4MODELOS MATEMATICOS DE LOS SISTEMAS
Representación gráfica de un sistema en
el dominio del tiempo
Diagrama Funcional
Control de velocidad de un auto.
Torque
Impulsor del Motor es proporcional a la apertura de la Mariposa del Carburador (y) y a las Revoluciones del Motor (nM): mMTorque en las Ruedas es proporcional al Torque Impulsor del Motor: mR
Fuerza de Empuje es proporcional al Torque en la Ruedas (mR): fA
Voltaje del Regulador de Velocidad es proporcional al Voltaje del Tacogenerador (ux) menos la Referencia (w) : uy
El voltaje del Tacogenerador es proporcional a las revoluciones del eje de la rueda del vehículo (x): nR
Слайд 5MODELOS MATEMATICOS DE LOS SISTEMAS
Representación gráfica de un sistema en
el dominio del tiempo
Diagrama Funcional
Control de velocidad de un auto.
La
Respuesta al Escalón de la Bobina del Regulador corresponde a un sistema de primer orden. El desplazamiento (S2) es proporcional a la Corriente de la Bobina del Regulador (i).
El desplazamiento (S1) es proporcional al desplazamiento (S2) .
La apertura de la compuerta de la mariposa del carburador es proporcional al desplazamiento negativo de (S1).
Слайд 6MODELOS MATEMATICOS DE LOS SISTEMAS
Representación gráfica de los sistemas en
el dominio del tiempo
Diagrama Funcional
Control de velocidad de un auto.
La
revolución del eje de la rueda del vehículo (nR) es proporcional a la velocidad del vehículo (x). La revolución del eje del motor (nM) es proporcional a la revolución del eje de la rueda del vehículo (nR).
De acuerdo a la ley de Newton la velocidad (x) del vehículo es proporcional a la integral de la Fuerza Resultante (fres)
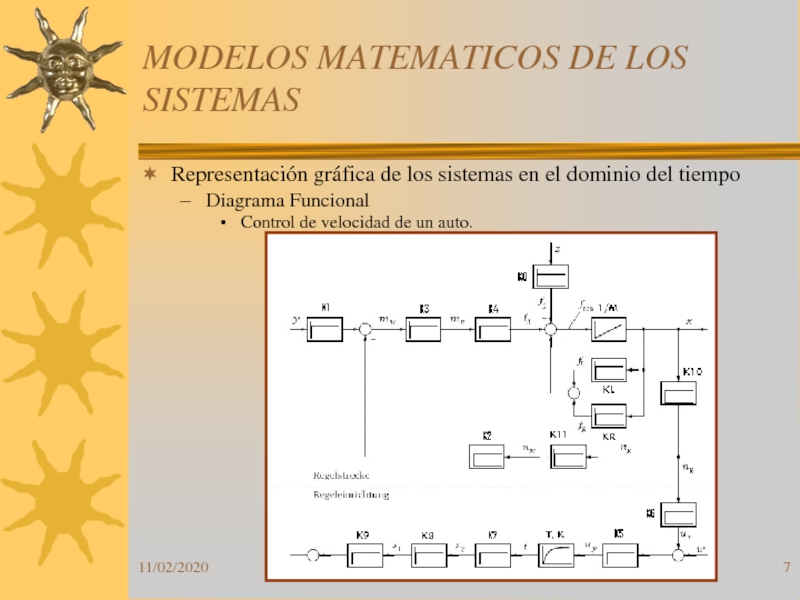
Слайд 7MODELOS MATEMATICOS DE LOS SISTEMAS
Representación gráfica de los sistemas en
el dominio del tiempo
Diagrama Funcional
Control de velocidad de un auto.
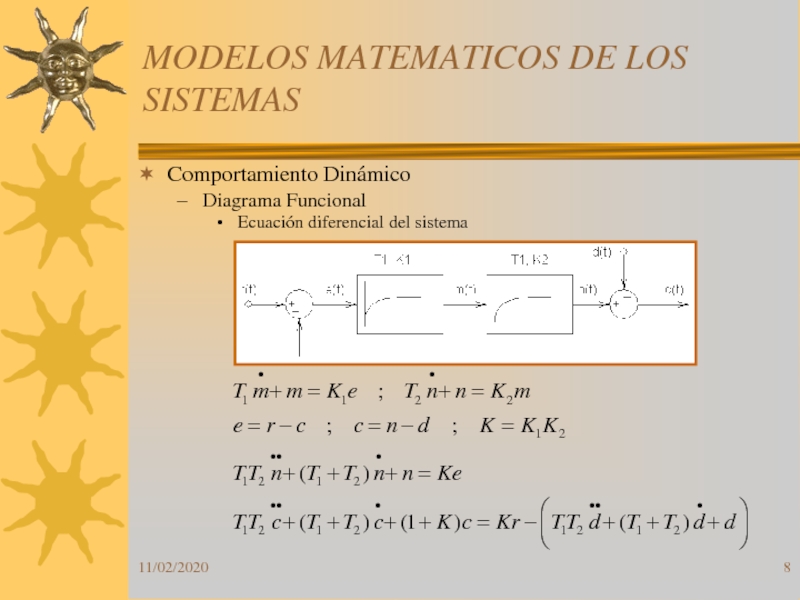
Слайд 8MODELOS MATEMATICOS DE LOS SISTEMAS
Comportamiento Dinámico
Diagrama Funcional
Ecuación diferencial del
sistema
Слайд 9MODELOS MATEMATICOS DE LOS SISTEMAS
Modelo del sistema es el resultado
del conocimiento referente a la transferencia, almacenamiento, conversión y disipación
de energía y en los métodos de interconexión de los elementos.Sistema Dinámico
Ecuaciones Diferenciales
Linearización
Transformada de Laplace (Función de Transferencia)
Sistemas físicos:
Eléctricos
Mecánicos de traslación y rotación
Hidráulicos
Térmicos
Neumáticos
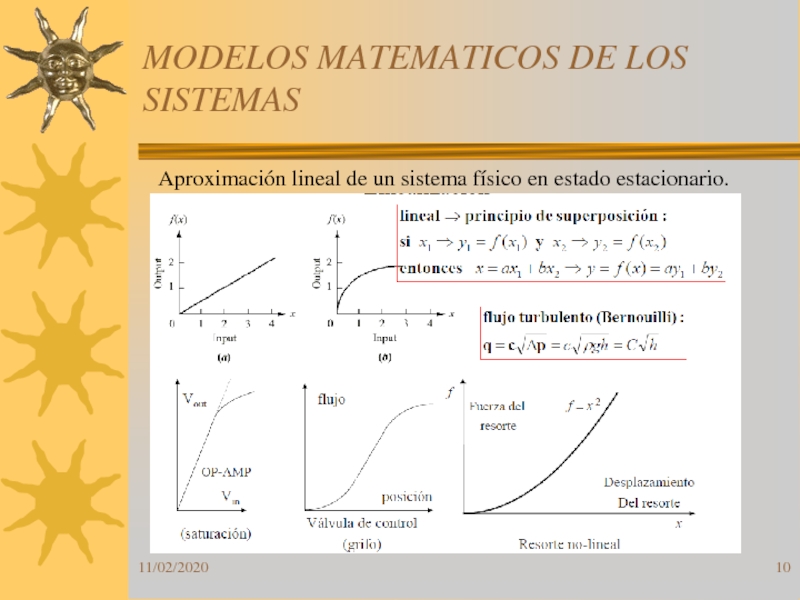
Слайд 10MODELOS MATEMATICOS DE LOS SISTEMAS
Aproximación lineal de un sistema físico
en estado estacionario.
Слайд 11MODELOS MATEMATICOS DE LOS SISTEMAS
Aproximación lineal de un sistema físico
en estado estacionario.
Desarrollo de la serie de Taylor en el
punto de operación de la curva continua en el intervalo de interésNOTA: a partir de ahora los valores incrementales se los representará sin el delta
Слайд 12MODELOS MATEMATICOS DE LOS SISTEMAS
Aproximación lineal de un sistema físico
Desarrollo
de la serie de Taylor en el punto de operación
de la curva continua en el intervalo de interésSi la variable dependiente depende de varias variables de excitación
Para la aproximación lineal de la serie de Taylor
Слайд 13MODELOS MATEMATICOS DE LOS SISTEMAS
Aproximación lineal de un sistema físico
Desarrollo
de la serie de Taylor en el punto de operación
de la curva continua en el intervalo de interésSi la variable dependiente depende de varias variables de excitación
Para la aproximación lineal de la serie de Taylor.
Слайд 14Comportamiento Estático de un Sistema
Comportamiento estático de un generador
Velocidad constante:
n
Voltaje de referencia: Uo=100
Corriente de
armadura: IAo=30Corriente de excitación: Ieo=0.6
Comportamiento del Regulador
MODELOS MATEMATICOS DE LOS SISTEMAS
Слайд 15Comportamiento Estático de un Sistema
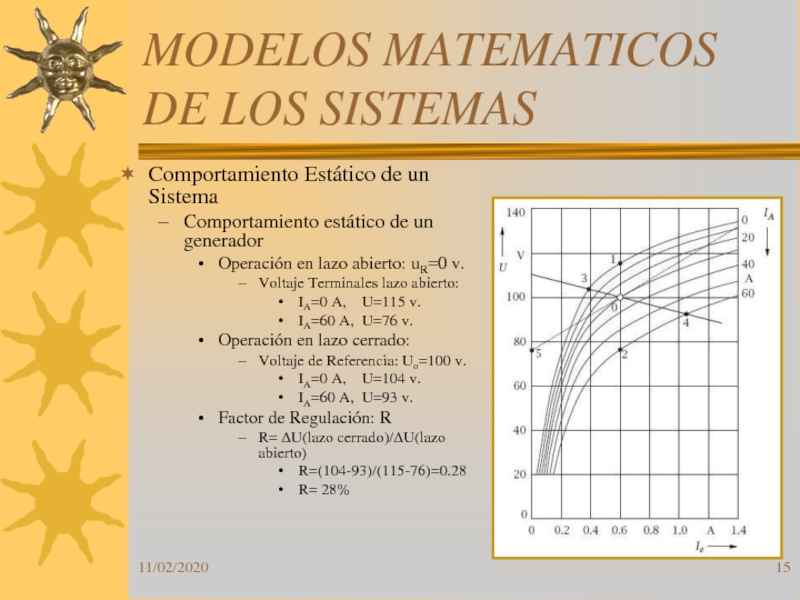
Comportamiento estático de un generador
Operación en
lazo abierto: uR=0 v.
Voltaje Terminales lazo abierto:
IA=0 A,
U=115 v.IA=60 A, U=76 v.
Operación en lazo cerrado:
Voltaje de Referencia: Uo=100 v.
IA=0 A, U=104 v.
IA=60 A, U=93 v.
Factor de Regulación: R
R= DU(lazo cerrado)/DU(lazo abierto)
R=(104-93)/(115-76)=0.28
R= 28%
MODELOS MATEMATICOS DE LOS SISTEMAS
Слайд 16MODELOS MATEMATICOS DE LOS SISTEMAS
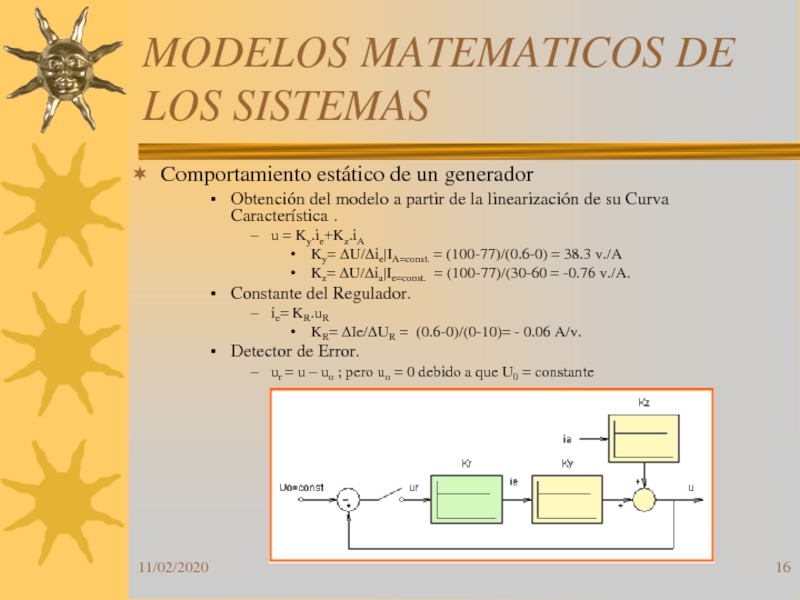
Comportamiento estático de un generador
Obtención
del modelo a partir de la linearización de su Curva
Característica .u = Ky.ie+Kz.iA
Ky= DU/Die|IA=const. = (100-77)/(0.6-0) = 38.3 v./A
Kz= DU/Dia|Ie=const. = (100-77)/(30-60 = -0.76 v./A.
Constante del Regulador.
ie= KR.uR
KR= DIe/DUR = (0.6-0)/(0-10)= - 0.06 A/v.
Detector de Error.
ur = u – uo ; pero uo = 0 debido a que U0 = constante
Слайд 17MODELOS MATEMATICOS DE LOS SISTEMAS
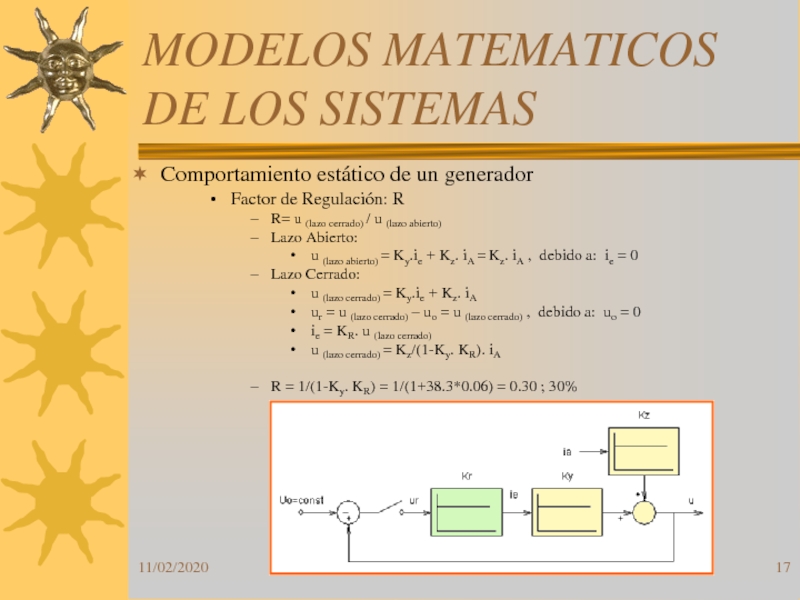
Comportamiento estático de un generador
Factor
de Regulación: R
R= u (lazo cerrado) / u (lazo abierto)
Lazo
Abierto: u (lazo abierto) = Ky.ie + Kz. iA = Kz. iA , debido a: ie = 0
Lazo Cerrado:
u (lazo cerrado) = Ky.ie + Kz. iA
ur = u (lazo cerrado) – uo = u (lazo cerrado) , debido a: uo = 0
ie = KR. u (lazo cerrado)
u (lazo cerrado) = Kz/(1-Ky. KR). iA
R = 1/(1-Ky. KR) = 1/(1+38.3*0.06) = 0.30 ; 30%
Слайд 18MODELOS MATEMATICOS DE LOS SISTEMAS
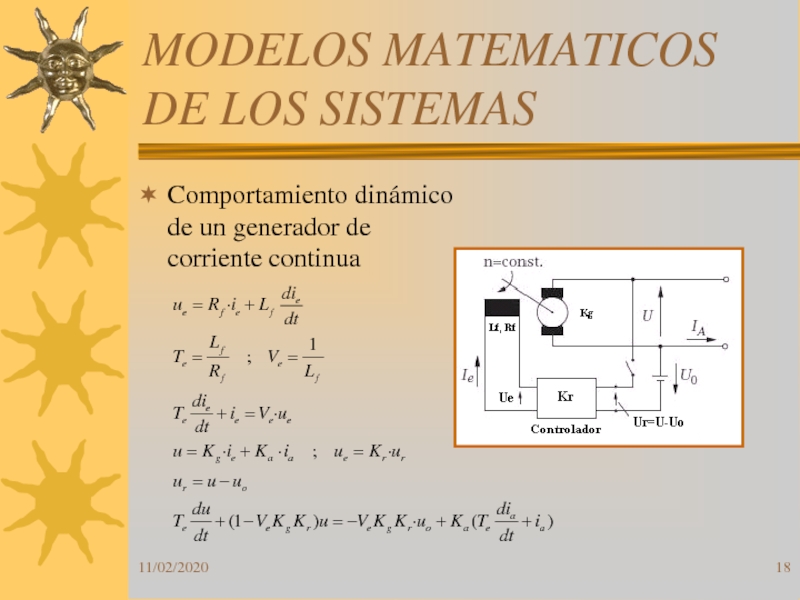
Comportamiento dinámico de un generador de
corriente continua
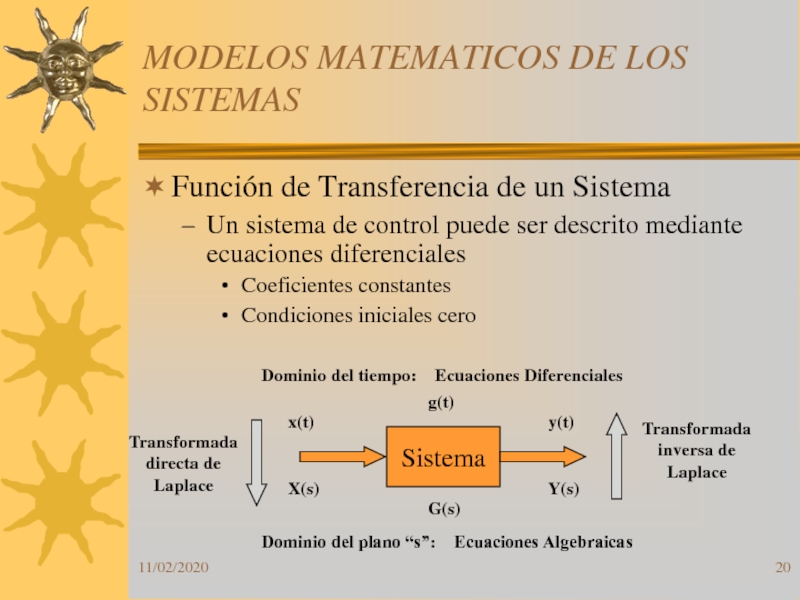
Слайд 20Función de Transferencia de un Sistema
Un sistema de control puede
ser descrito mediante ecuaciones diferenciales
Coeficientes constantes
Condiciones iniciales cero
MODELOS MATEMATICOS DE
LOS SISTEMASSistema
x(t)
y(t)
g(t)
X(s)
G(s)
Y(s)
Dominio del tiempo: Ecuaciones Diferenciales
Dominio del plano “s”: Ecuaciones Algebraicas
Transformada
directa de
Laplace
Transformada
inversa de
Laplace
Слайд 21MODELOS MATEMATICOS DE LOS SISTEMAS
Función de Transferencia de un Sistema
Un
sistema de control puede ser descrito mediante ecuaciones diferenciales
Coeficientes constantes
Condiciones
iniciales ceroTransformada
de Laplace
Слайд 22MODELOS MATEMATICOS DE LOS SISTEMAS
Función de Transferencia de un Sistema
Transformada
inversa
de
Laplace
“Multiplicación”
“Convolución”
Слайд 23Aproximación lineal de un sistema físico
La gran mayoría de sistemas
físicos se comportan como lineales dentro de algún intervalo de
las variables.Cuando el sistema está en reposo, para ser considerado lineal debe cumplir:
Con el teorema de superposición y homogeneidad
MODELOS MATEMATICOS DE LOS SISTEMAS
Sistema
x(t)
x1(t)+x2(t)
bx(t)
y(t)
y1(t)+y2(t)
by(t)
Слайд 24MODELOS MATEMATICOS DE LOS SISTEMAS
Motor de Corriente Continua
El estator, inductor
Carcasa
Polos
principales y auxiliares
Devanado inductor
El rotor, inducido
Colector, delgas
Devanado inducido
Núcleo del inducido
Las
escobillas.Слайд 25MODELOS MATEMATICOS DE LOS SISTEMAS
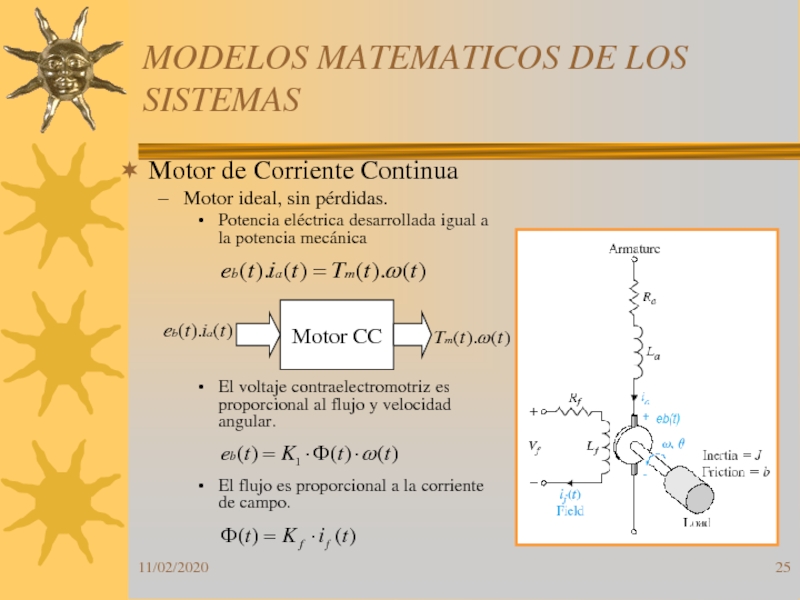
Motor de Corriente Continua
Motor ideal, sin
pérdidas.
Potencia eléctrica desarrollada igual a la potencia mecánica
El voltaje contraelectromotriz
es proporcional al flujo y velocidad angular.El flujo es proporcional a la corriente de campo.
Motor CC
Слайд 27MODELOS MATEMATICOS DE LOS SISTEMAS
Motor de Corriente Continua
Motor ideal, sin
pérdidas.
Se presentan dos casos:
Mantener constante la corriente de campo, “control
de armadura”Mantener constante la corriente de armadura, “control de campo”
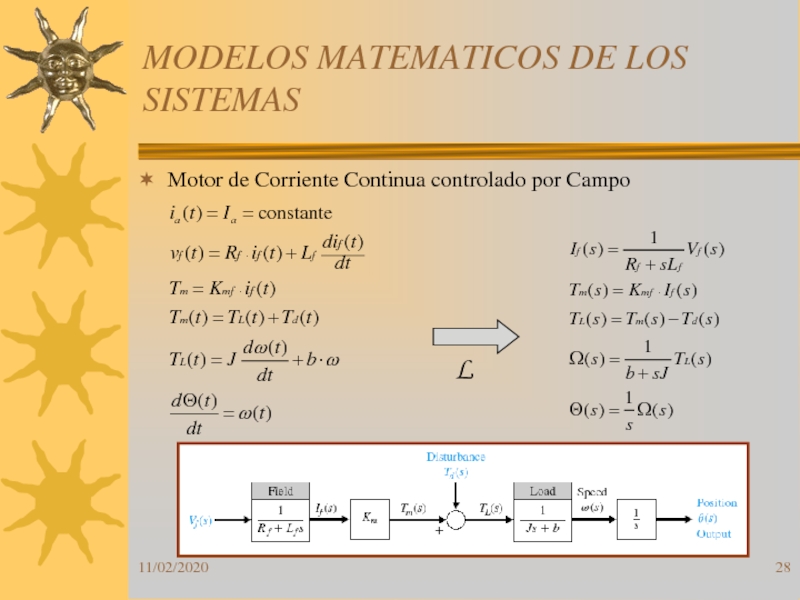
Слайд 29MODELOS MATEMATICOS DE LOS SISTEMAS
Motor de Corriente Continua controlado por
Campo
Ia constante
Función de transferencia
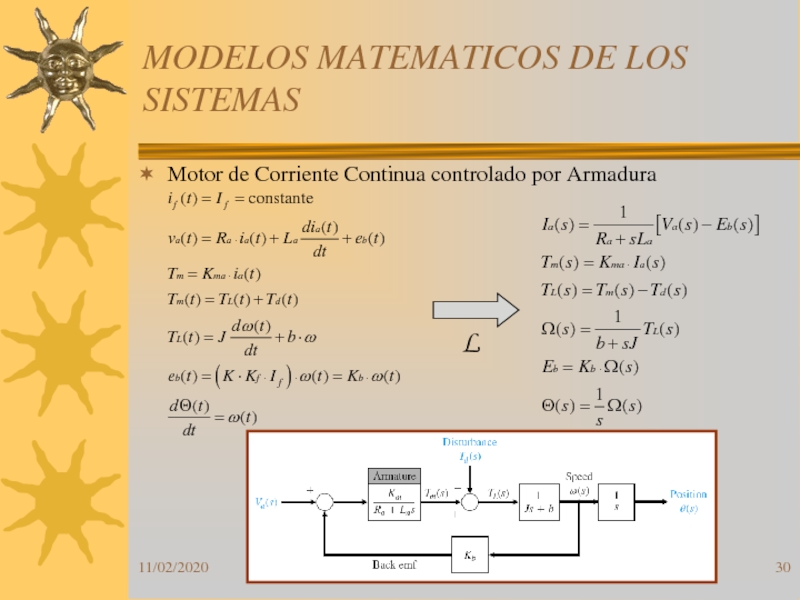
Слайд 31MODELOS MATEMATICOS DE LOS SISTEMAS
Motor de Corriente Continua controlado por
Armadura
If constante
Función de transferencia
Слайд 32Amplificador Rotativo de dos Etapas, Amplidina
NOTA: El flujo de reacción
de armadura es compensado por el flujo de la bobina
LdMODELOS MATEMATICOS DE LOS SISTEMAS
Слайд 33MODELOS MATEMATICOS DE LOS SISTEMAS
Regulador Hidráulico, servomotor hidráulico
Q Caudal del aceite
P
Diferencia de presión
x Desplazamiento de la válvula de control
y Desplazamiento del cilindro
de potenciaСлайд 34MODELOS MATEMATICOS DE LOS SISTEMAS
Regulador Hidráulico, servomotor hidráulico
A Superficie del pistón
de
La Función de Transferencia:
L
Слайд 35MODELOS MATEMATICOS DE LOS SISTEMAS
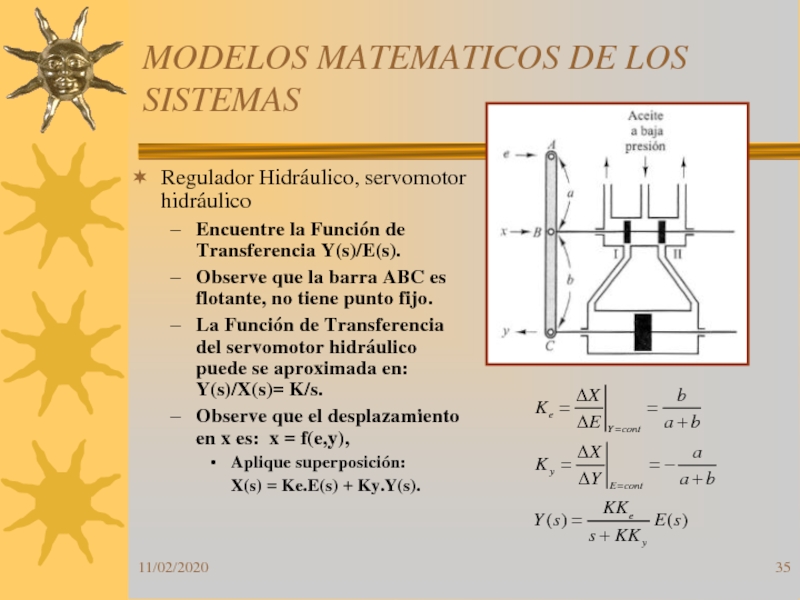
Regulador Hidráulico, servomotor hidráulico
Encuentre la Función
de Transferencia Y(s)/E(s).
Observe que la barra ABC es flotante,
no tiene punto fijo. La Función de Transferencia del servomotor hidráulico puede se aproximada en: Y(s)/X(s)= K/s.
Observe que el desplazamiento en x es: x = f(e,y),
Aplique superposición:
X(s) = Ke.E(s) + Ky.Y(s).
Слайд 36MODELOS MATEMATICOS DE LOS SISTEMAS
Sistema de engranajes
Sistema ideal, potencia de
entrada es igual a la potencia de salida, no tiene
pérdidasLos dos engranajes recorren la misma distancia lineal
El tamaño de los dientes es igual en ambos engranajes
La velocidad angular es proporcional al desplazamiento angular en cada engranaje
Слайд 37Sistema de engranajes
Se incluye la fricción viscosa y la inercia
Referir
el sistema al eje del motor
MODELOS MATEMATICOS DE LOS SISTEMAS
Слайд 38MODELOS MATEMATICOS DE LOS SISTEMAS
Sistema Hidráulico
Sistema ideal, potencia de entrada
es igual a la potencia de salida.
La presión hidráulica es
la misma, principio de Pascal.Слайд 39Detector de Error utilizando Potenciómetros
Potenciómetros de 360o, sin tope
MODELOS MATEMATICOS
DE LOS SISTEMAS
Слайд 41MODELOS MATEMATICOS DE LOS SISTEMAS
Sistema Térmico
La variación de la temperatura
de salida alrededor de su punto de operación podrá ser
debida a un cambio en el calor suministrado por el calentador o por un cambio en la temperatura del fluido entrante.Balance Energético
qe(t) Calor suministrado por calentador
qi(t) Calor del fluido entrante
ql(t) Calor absorvido por fluido
qs(t) Calor a traves de paredes
Ct Capacidad térmica kcal/°C
Rt Resistencia térmica °C.s/kcal
F Flujo líquido kg/s
c Calor específico kcal/kg.°C
Слайд 43MODELOS MATEMATICOS DE LOS SISTEMAS
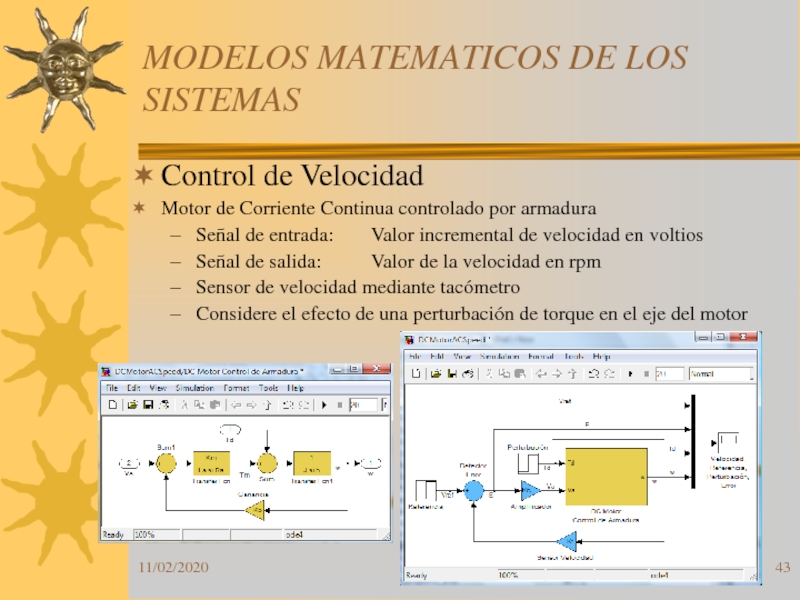
Control de Velocidad
Motor de Corriente Continua
controlado por armadura
Señal de entrada: Valor incremental de velocidad en voltios
Señal
de salida: Valor de la velocidad en rpmSensor de velocidad mediante tacómetro
Considere el efecto de una perturbación de torque en el eje del motor
Слайд 44MODELOS MATEMATICOS DE LOS SISTEMAS
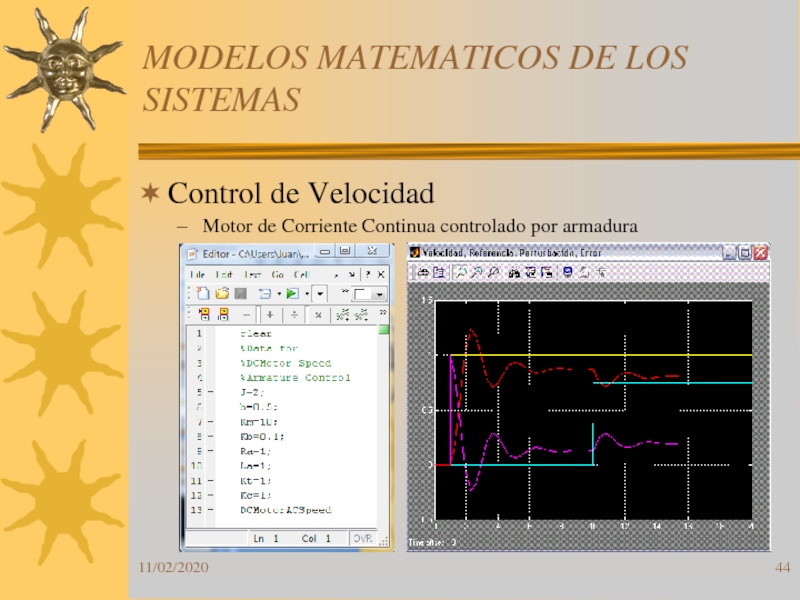
Control de Velocidad
Motor de Corriente Continua
controlado por armadura
Слайд 45MODELOS MATEMATICOS DE LOS SISTEMAS
Control de Posición
Motor de Corriente Continua
controlado por armadura
Señal de entrada: Posición eje de entrada
Señal de salida: Posición
eje de salidaDetector de error a base de potenciómetros
Considere el efecto de la inercia y fricción de la carga conectada al eje del motor mediante engranajes
Слайд 46MODELOS MATEMATICOS DE LOS SISTEMAS
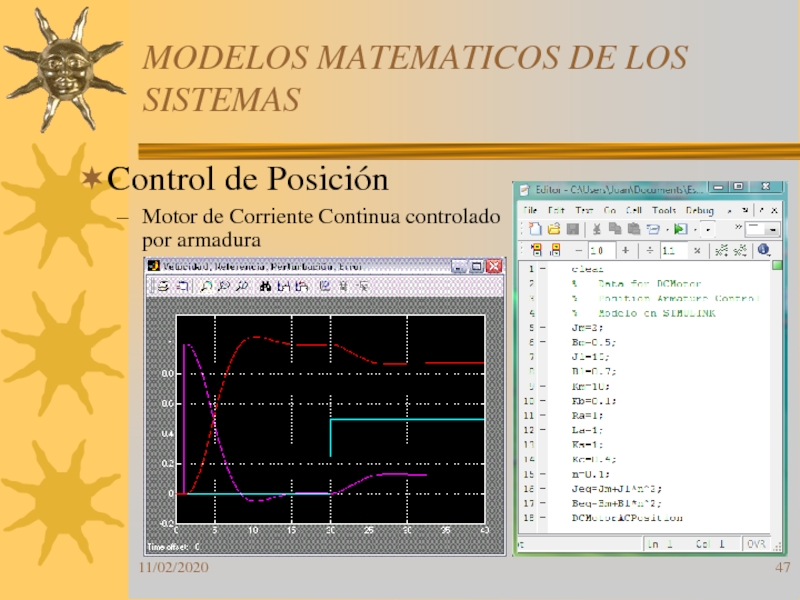
Control de Posición
Motor de Corriente Continua
controlado por armadura
Simulación del sistema utilizando MATLAB y SIMULINK
Incluya el
efecto de una perturbación de torqueСлайд 47MODELOS MATEMATICOS DE LOS SISTEMAS
Control de Posición
Motor de Corriente Continua
controlado por armadura
Слайд 48Modelos de diagramas de bloques
Los diagramas de bloques son bloques
operacionales y unidireccionales que representan la función de transferencia de
las variables de interésPara representar un sistema con diferentes variables bajo control, se utiliza una interconexión de bloques
La transformaciones de diagramas de bloques y las técnicas de reducción se las obtiene aplicando el algebra de las variables del diagrama
MODELOS MATEMATICOS DE LOS SISTEMAS
Слайд 49MODELOS MATEMATICOS DE LOS SISTEMAS
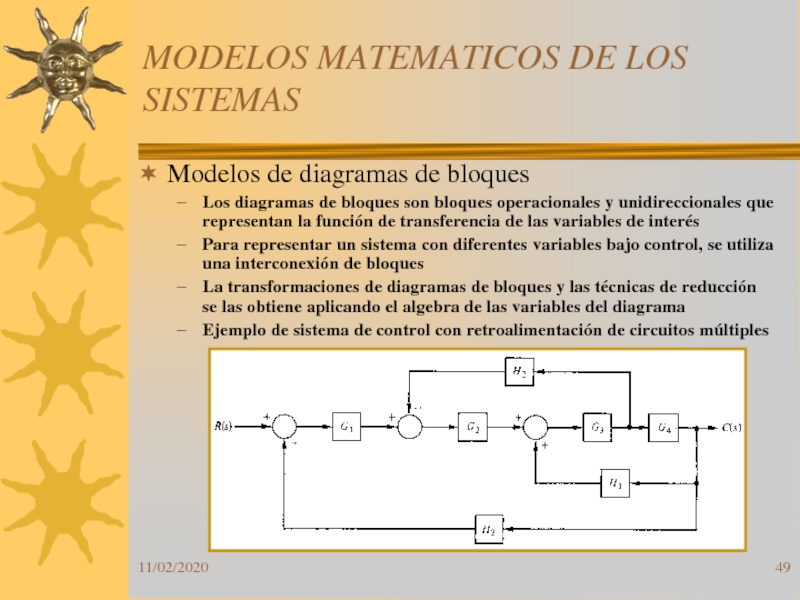
Modelos de diagramas de bloques
Los diagramas
de bloques son bloques operacionales y unidireccionales que representan la
función de transferencia de las variables de interésPara representar un sistema con diferentes variables bajo control, se utiliza una interconexión de bloques
La transformaciones de diagramas de bloques y las técnicas de reducción se las obtiene aplicando el algebra de las variables del diagrama
Ejemplo de sistema de control con retroalimentación de circuitos múltiples
Слайд 50MODELOS MATEMATICOS DE LOS SISTEMAS
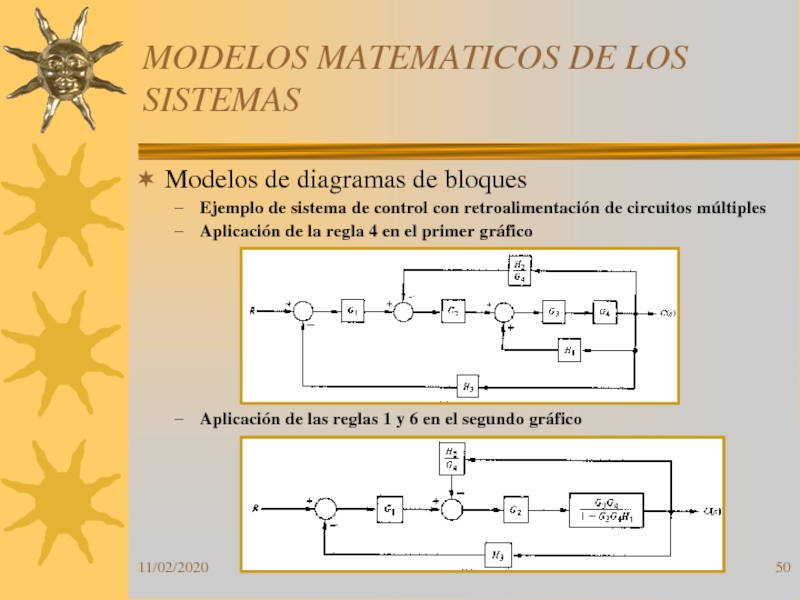
Modelos de diagramas de bloques
Ejemplo de
sistema de control con retroalimentación de circuitos múltiples
Aplicación de la
regla 4 en el primer gráficoAplicación de las reglas 1 y 6 en el segundo gráfico
Слайд 51MODELOS MATEMATICOS DE LOS SISTEMAS
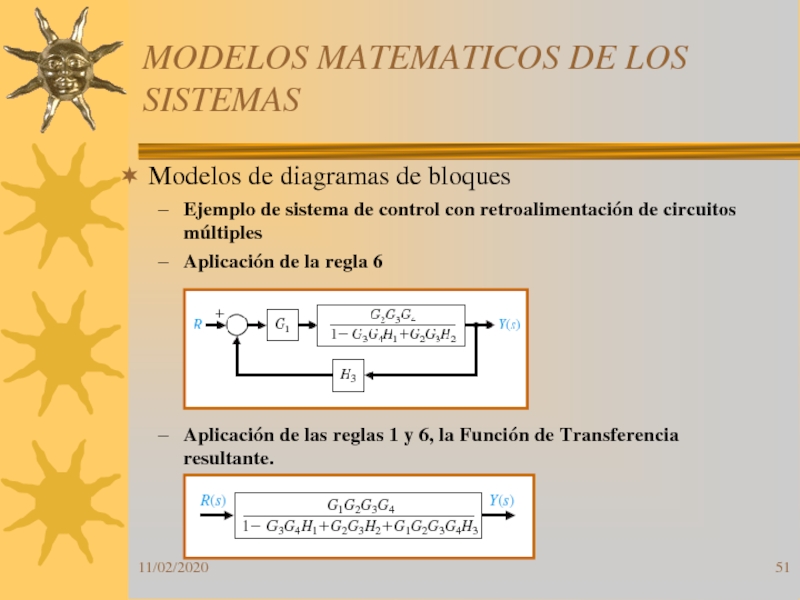
Modelos de diagramas de bloques
Ejemplo de
sistema de control con retroalimentación de circuitos múltiples
Aplicación de la
regla 6 Aplicación de las reglas 1 y 6, la Función de Transferencia resultante.
Слайд 52Gráficos de Flujo de Señal
Una gráfica de flujo de señales
puede definirse como un método gráfico para representar las relaciones
entrada-salida entre las variables de un sistema de ecuaciones algebraicas lineales.Es una representación causa y efecto de los sistemas lineales.
En los gráficos de flujo de señales se usan puntos de enlace o nodos para representar las variables y se los interconecta mediante segmentos lineales llamados ramas de acuerdo a las ecuaciones de causa y efecto.
Las ramas tienen ganancia y dirección asociadas a ellas.
MODELOS MATEMATICOS DE LOS SISTEMAS
x1
x2
a
Слайд 53MODELOS MATEMATICOS DE LOS SISTEMAS
Gráficos de Flujo de Señal
Representación causa
y efecto de los sistemas lineales.
Los sistemas pueden ser o
no ser bidireccionales.Una resistencia, bidireccional
Un amplificador, (amplificador operacional ideal ), direccional
Ganancia infinita, impedancia de entrada infinita, impedancia de salida cero.
Слайд 54MODELOS MATEMATICOS DE LOS SISTEMAS
Gráficos de Flujo de Señal
Definiciones:
Nudo
Un punto
que representa una señal
Transmitancia
Una ganancia entre dos puntos
Rama
Une dos nudos
y tiene direcciónNudo de Entrada
Solo tiene ramas que salen
Nudo de Salida
Solo tiene ramas que entran
Nudo Mixto
Tiene ramas que entran y salen
Lazo
Es un camino cerrado
Lazos Distintos
No tiene nudos comunes
Trayecto Directo
Va desde nudo de entrada al nudo de salida pasando una sola vez por cada nudo
Ganancia de Trayecto Directo
Producto de las transmitancias de las ramas del trayecto directo
Слайд 55MODELOS MATEMATICOS DE LOS SISTEMAS
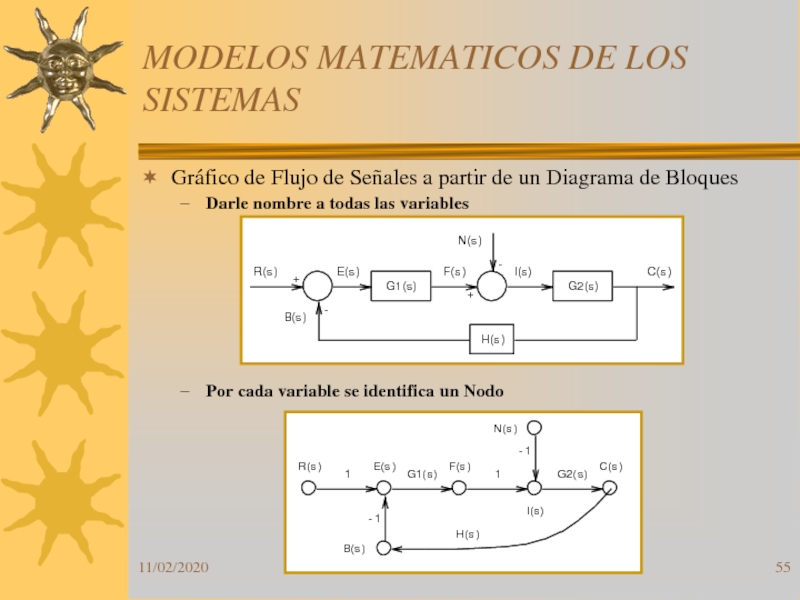
Gráfico de Flujo de Señales a
partir de un Diagrama de Bloques
Darle nombre a todas las
variablesPor cada variable se identifica un Nodo
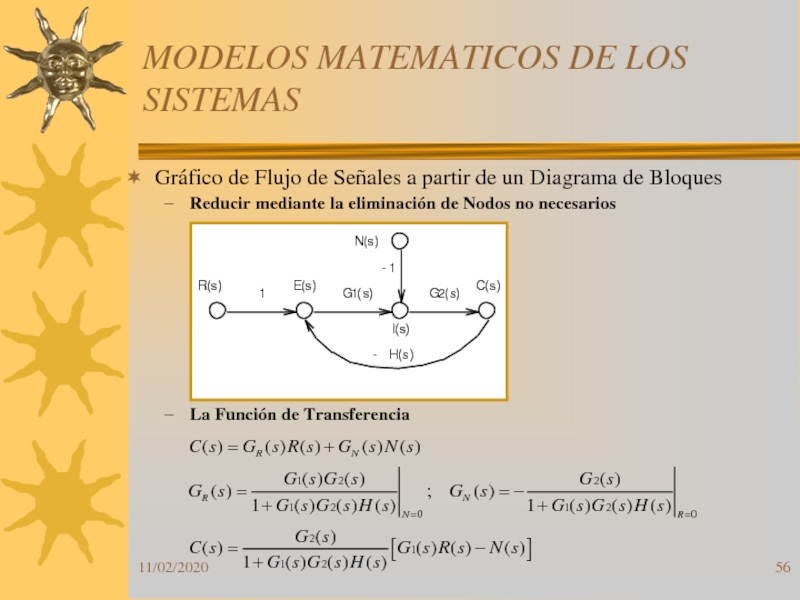
Слайд 56MODELOS MATEMATICOS DE LOS SISTEMAS
Gráfico de Flujo de Señales a
partir de un Diagrama de Bloques
Reducir mediante la eliminación de
Nodos no necesariosLa Función de Transferencia
Слайд 57Resolución de Gráficos de Flujo de Señales mediante el método
de Mason
MODELOS MATEMATICOS DE LOS SISTEMAS
Consideremos el siguiente ejemplo:
El sistema
se lo puede describir mediante el siguiente conjunto de ecuacionesEmpleando la regla de Cramer
Слайд 58MODELOS MATEMATICOS DE LOS SISTEMAS
Resolución de Gráficos de Flujo de
Señales mediante el método de Mason
En forma general, la ganancia
lineal Tij entre la variable independiente xi (variable de entrada) y una variable dependiente xj (variable de salida) está dada por la siguiente expresión, fórmula de Mason:n Números de trayectos directos entre la entrada xi y la salida xj
Pijk Ganancia de la trayectoria directa k
D Determinante del grafo
Dijk Cofactor del trayecto directo Pijk (es el determinante del grafo en el que se han removido los elementos del trayecto directo k)
Слайд 59MODELOS MATEMATICOS DE LOS SISTEMAS
Resolución de Gráficos de Flujo de
Señales mediante el método de Mason
D Determinante del grafo
Sumatoria de todas
las ganancias de lazoSumatoria del producto de las ganancias de todas las combinaciones posibles de los lazos distintos de dos en dos.
Igual que el caso anterior pero para los lazos distintos de tres en tres.
Слайд 60MODELOS MATEMATICOS DE LOS SISTEMAS
Resolución de Gráficos de Flujo de
Señales mediante el método de Mason
Consideremos el siguiente sistema
Se desea
obtener la Función de Transferencia Y(s)/R(s)Número de caminos directos: 3
Número de lazos: 8
Número de lazos distintos: 4
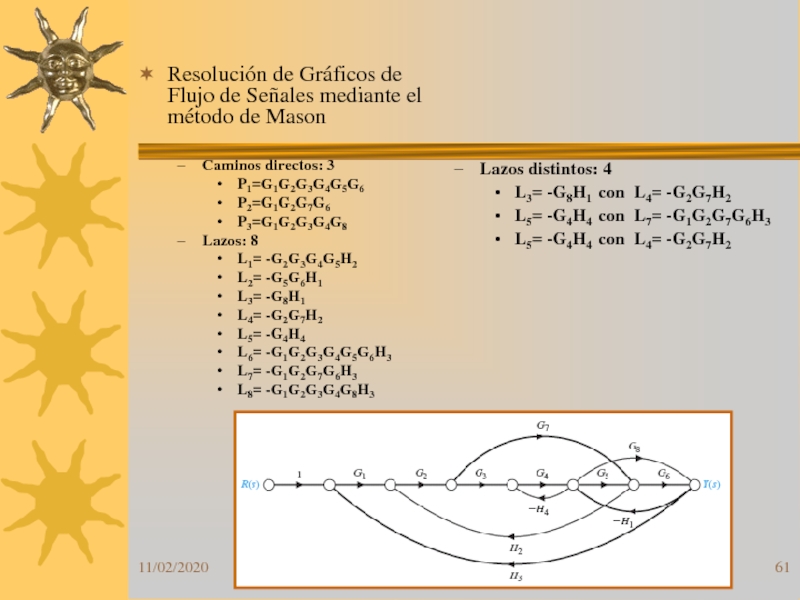
Слайд 61Resolución de Gráficos de Flujo de Señales mediante el método
de Mason
Caminos directos: 3
P1=G1G2G3G4G5G6
P2=G1G2G7G6
P3=G1G2G3G4G8
Lazos: 8
L1= -G2G3G4G5H2
L2= -G5G6H1
L3= -G8H1
L4= -G2G7H2
L5= -G4H4
L6=
-G1G2G3G4G5G6H3L7= -G1G2G7G6H3
L8= -G1G2G3G4G8H3
Lazos distintos: 4
L3= -G8H1 con L4= -G2G7H2
L5= -G4H4 con L7= -G1G2G7G6H3
L5= -G4H4 con L4= -G2G7H2
Слайд 62MODELOS MATEMATICOS DE LOS SISTEMAS
Resolución de Gráficos de Flujo de
Señales mediante el método de Mason
El determinante del sistema:
D=1-(L1+L2+L3+L4+L5+L6+L7+L8)+(L3L4+L5L7+L5L4)Los cofactores:
Para P1 es D1=1
Para P2 es D2=1-L5
Para P3 es D3=1
Finalmente, la Función de Trasferencia:
Слайд 63Comandos de MATLAB
Generación de una función de transferencia
Suma de funciones
de transferencias
Obtención de los Polos
Obtención de los Ceros
Gráfico de los
Polos y CerosEjemplo 2.16
MODELOS MATEMATICOS DE LOS SISTEMAS
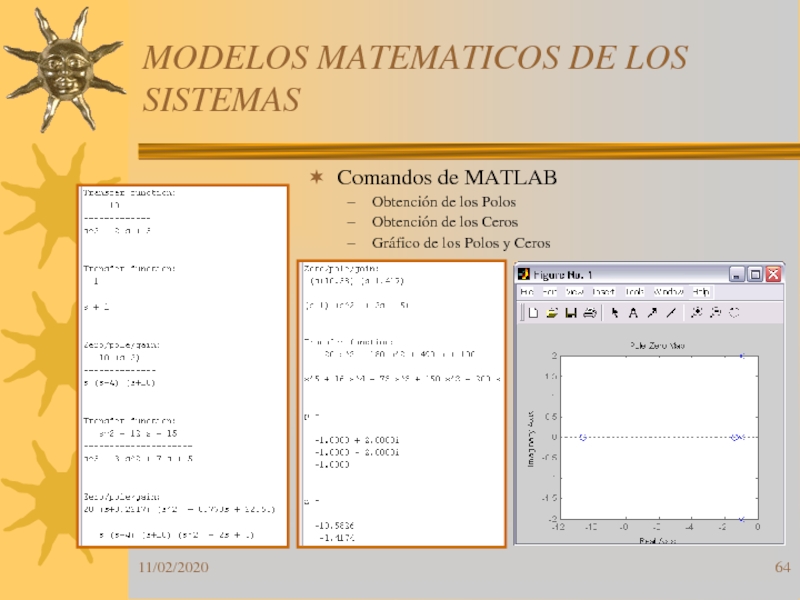
Слайд 64MODELOS MATEMATICOS DE LOS SISTEMAS
Comandos de MATLAB
Obtención de los Polos
Obtención
de los Ceros
Gráfico de los Polos y Ceros
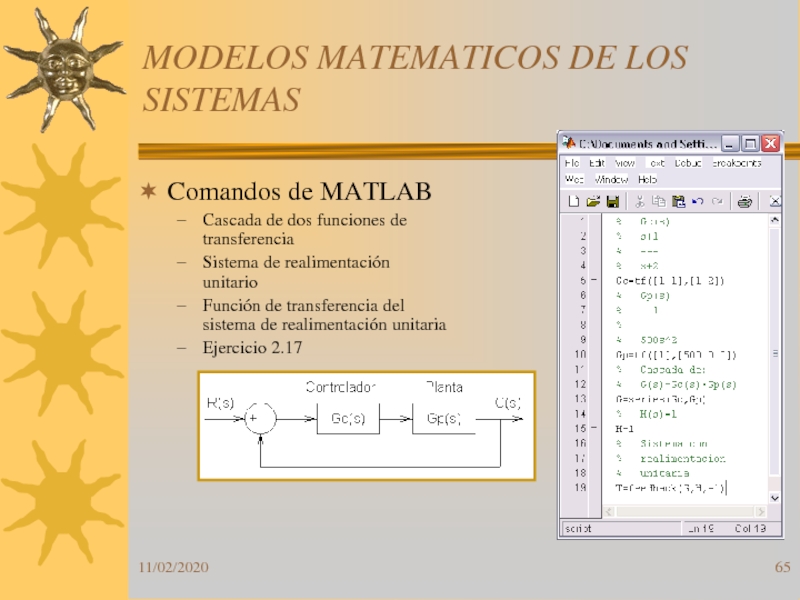
Слайд 65MODELOS MATEMATICOS DE LOS SISTEMAS
Comandos de MATLAB
Cascada de dos funciones
de transferencia
Sistema de realimentación unitario
Función de transferencia del sistema de
realimentación unitariaEjercicio 2.17
Слайд 66MODELOS MATEMATICOS DE LOS SISTEMAS
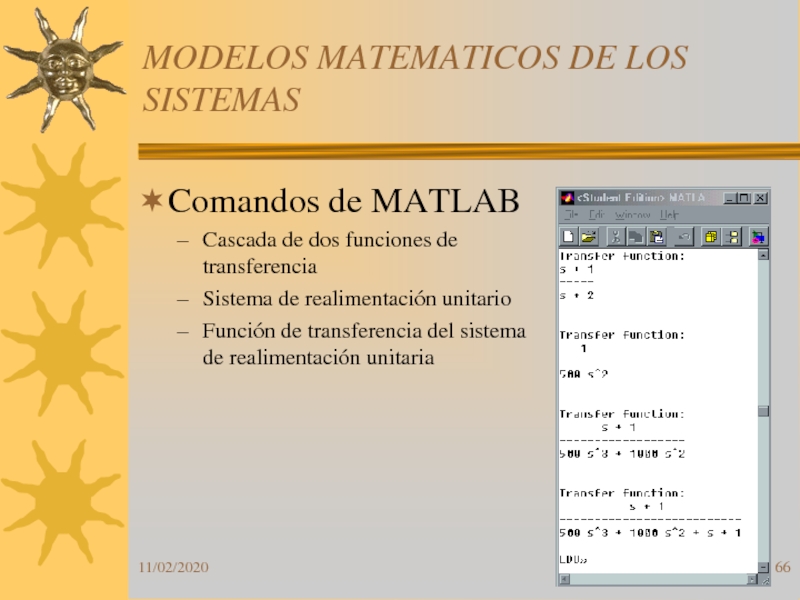
Comandos de MATLAB
Cascada de dos funciones
de transferencia
Sistema de realimentación unitario
Función de transferencia del sistema de
realimentación unitariaСлайд 67Comandos de MATLAB
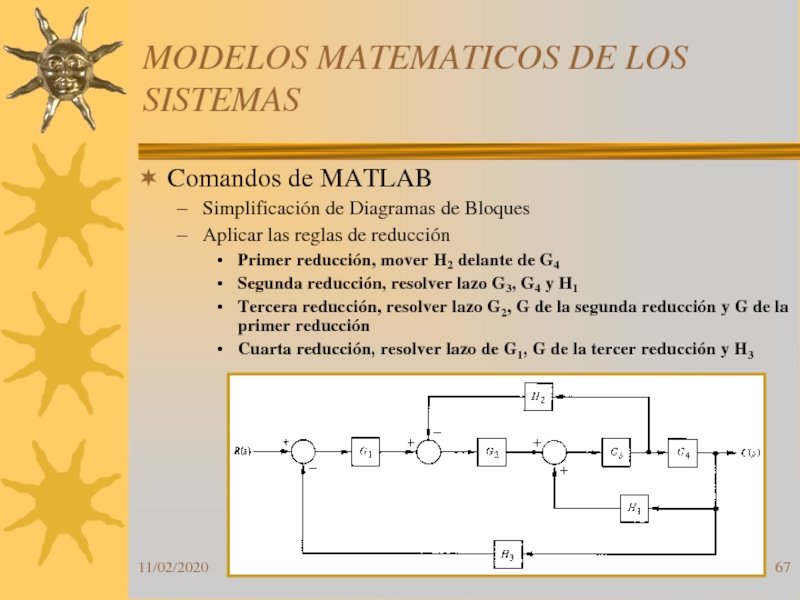
Simplificación de Diagramas de Bloques
Aplicar las reglas de
reducción
Primer reducción, mover H2 delante de G4
Segunda reducción, resolver lazo
G3, G4 y H1Tercera reducción, resolver lazo G2, G de la segunda reducción y G de la primer reducción
Cuarta reducción, resolver lazo de G1, G de la tercer reducción y H3
MODELOS MATEMATICOS DE LOS SISTEMAS
Слайд 68MODELOS MATEMATICOS DE LOS SISTEMAS
Comandos de MATLAB
Simplificación de Diagramas de
Bloques
Aplicar las reglas de reducción
Ejercicio 2.20
Primer reducción, mover H2 delante
de G4Segunda reducción, resolver lazo G3, G4 y H1
Tercera reducción, resolver lazo G2, G de la segunda reducción y G de la primer reducción
Cuarta reducción, resolver lazo de G1, G de la tercer reducción y H3
Слайд 69MODELOS MATEMATICOS DE LOS SISTEMAS
Comandos de MATLAB
Simplificación de Diagramas de
Bloques
Aplicar las reglas de reducción
Primer reducción, mover H2 delante de
G4Segunda reducción, resolver lazo G3, G4 y H1
Tercera reducción, resolver lazo G2, G de la segunda reducción y G de la primer reducción
Cuarta reducción, resolver lazo de G1, G de la tercer reducción y H3
Слайд 70MODELOS MATEMATICOS DE LOS SISTEMAS
Comandos de MATLAB
Simplificación de Diagramas de
Bloques
Aplicar las reglas de reducción
Simplificación de la función de transferencia
al eliminar los polos y ceros de igual valor.Uso de la función “minreal”