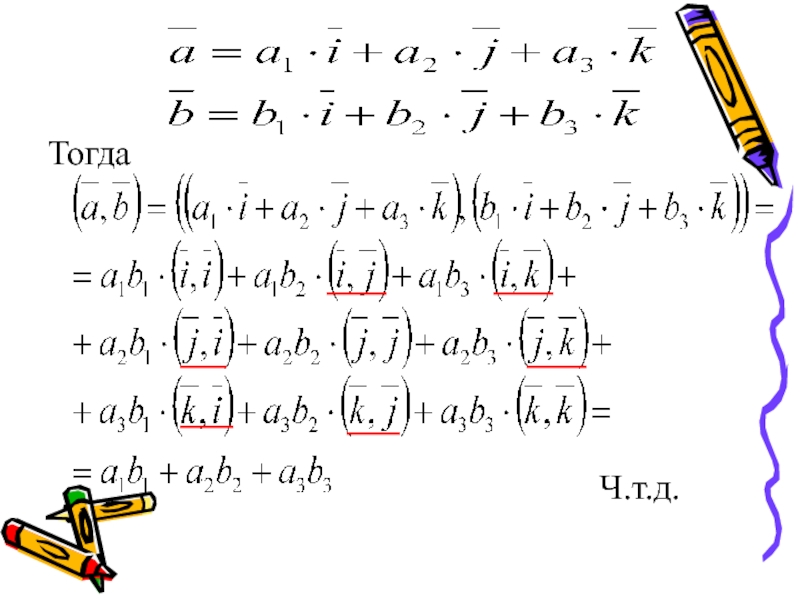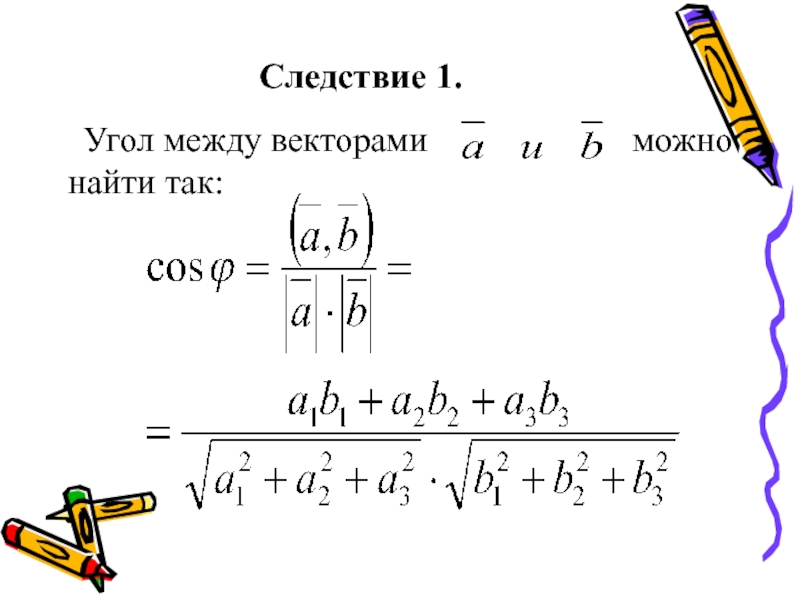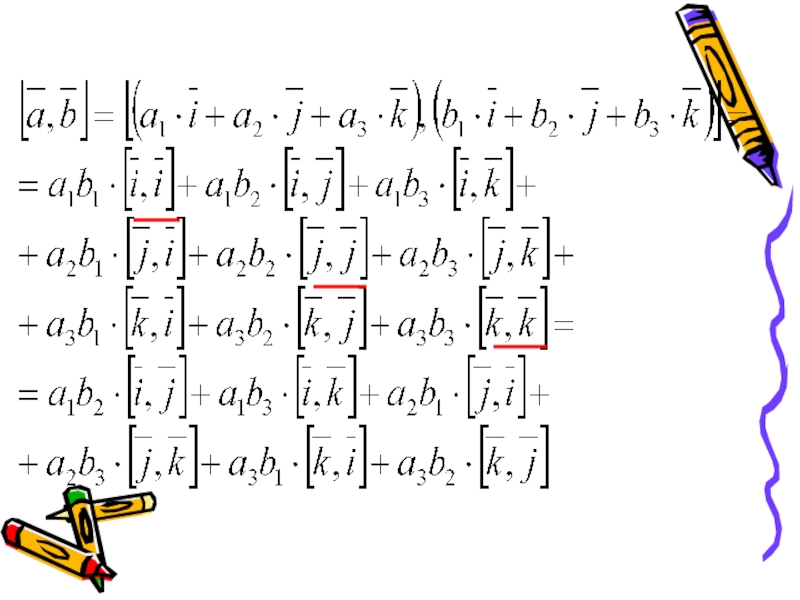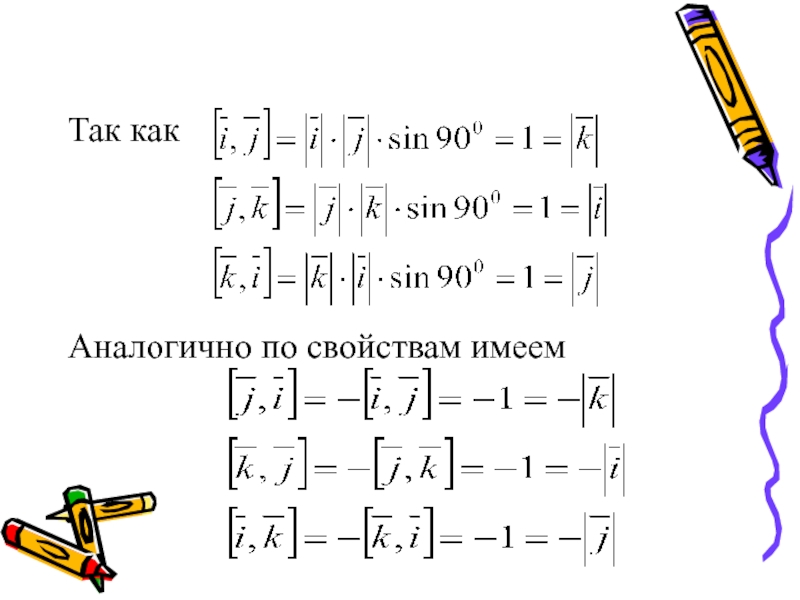Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Действия над векторами
Содержание
- 1. Действия над векторами
- 2. Векторы можно:Складывать;Вычитать;Умножать на ненулевое число;Умножать вектор на вектор (скалярно, векторно, смешанно)
- 3. П.1. Сложение векторовПусть даны векторы
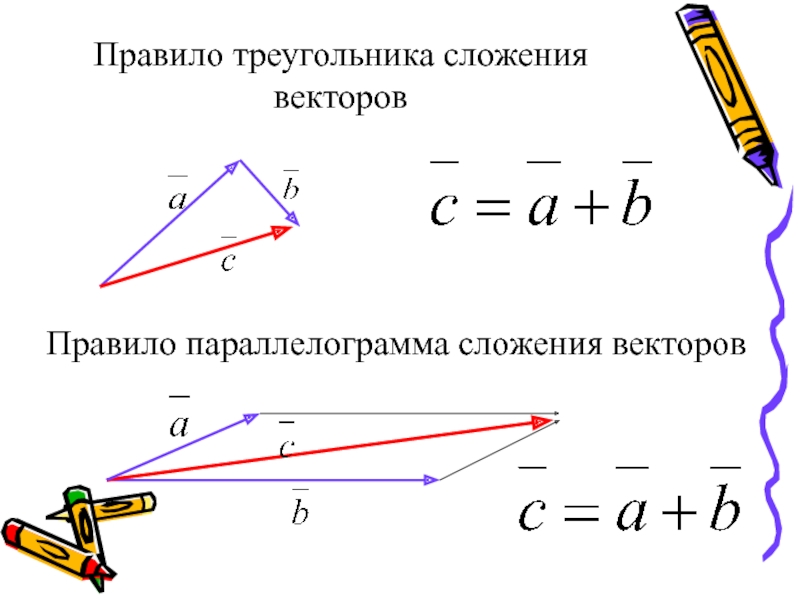
- 4. Правило треугольника сложения векторовПравило параллелограмма сложения векторов
- 5. Свойства сложения векторов
- 6. П.2. Вычитание векторовПусть даны векторы
- 7. П.3. Умножение вектора на ненулевое числоПусть дан
- 8. Свойства умножения вектора на число
- 9. П.4. Умножение векторовА) Скалярное произведение двух векторовСкалярным
- 10. Свойства скалярного произведения
- 11. Теорема Пусть в ортонормированном базисе
- 12. Тогда Ч.т.д.
- 13. Следствие 1.Угол между векторами
- 14. Следствие 2Векторы
- 15. В) Векторное произведение векторовТройка векторов
- 16. Векторным произведением векторов
- 17. Свойства векторного произведения5. Площадь параллелограмма, построенного на
- 18. ТеоремаПусть в ортонормированном базисе
- 19. Доказательство:Разложим данные векторы по базисным векторам, тогда получимНайдем векторное произведение данных векторов.
- 20. Слайд 20
- 21. Так как Аналогично по свойствам имеем
- 22. Тогда с учетом данных равенств имеем:Ч.т.д.
- 23. С) Смешанное произведение трех векторовСмешанным произведением векторов
- 24. Свойства смешанного произведенияВекторы
- 25. Теорема Пусть даны векторы
- 26. Доказательство:Так как по определению смешанное произведение есть
- 27. В результате вычисления данного определителя, находим координаты
- 28. Линейная комбинация векторов
- 29. Векторы
- 30. Замечание 1Если хотя бы один из векторов
- 31. Теорема 1Необходимым и достаточным условием линейной зависимости
- 32. Теорема 2Необходимым и достаточным условием линейной зависимости
- 33. Теорема 3Любые четыре вектора линейно зависимы.Утверждение 1Любая
- 34. Скачать презентанцию
Векторы можно:Складывать;Вычитать;Умножать на ненулевое число;Умножать вектор на вектор (скалярно, векторно, смешанно)
Слайды и текст этой презентации
Слайд 2Векторы можно:
Складывать;
Вычитать;
Умножать на ненулевое число;
Умножать вектор на вектор (скалярно, векторно,
смешанно)
Слайд 3П.1. Сложение векторов
Пусть даны векторы
и
Тогда суммой
данных векторов будет вектор , координаты которого найдем так:
Сложение векторов можно произвести по правилу треугольника или по правилу параллелограмма.
Слайд 6П.2. Вычитание векторов
Пусть даны векторы
и
Тогда разностью данных векторов будет
вектор координаты которого найдем так:
Слайд 7П.3. Умножение вектора на ненулевое число
Пусть дан вектор
. Тогда
произведением данного вектора на число называют вектор,для которого выполнено:
Векторы и коллинеарные;
;
Векторы , если k>0
векторы , если k<0
Слайд 9П.4. Умножение векторов
А) Скалярное произведение двух векторов
Скалярным произведением двух векторов
называют число равное произведению длин этих векторов на косинус угла
между ними.Пусть даны векторы и
Тогда их скалярное произведение равно:
Слайд 11Теорема
Пусть в ортонормированном базисе
даны векторы
и . Тогда их скалярное произведение найдем по формуле:Доказательство: разложим данные векторы по базису .Тогда получим:
Слайд 14Следствие 2
Векторы
и
перпендикулярны тогда и только тогда, когда .Следствие 3
Ненулевые векторы и параллельны тогда и только тогда, когда
Слайд 15В) Векторное произведение векторов
Тройка векторов
называется упорядоченной, если известно какой из них
является первым, вторым и третьим.Упорядоченная тройка векторов является правой, если после приведения их к общему началу кратчайший поворот от первого ко второму вектору из конца третьего вектора виден против часовой стрелки. Иначе, тройка векторов – левая.
1
2
3
Слайд 17Свойства векторного произведения
5. Площадь параллелограмма, построенного на векторах
и равна длине вектора
Слайд 18Теорема
Пусть в ортонормированном базисе даны векторы
и
. Тогда их векторное произведение найдем по формуле:
Слайд 19Доказательство:
Разложим данные векторы по базисным векторам, тогда получим
Найдем векторное произведение
данных векторов.
Слайд 23С) Смешанное произведение трех векторов
Смешанным произведением векторов
Слайд 24Свойства смешанного произведения
Векторы компланарны
тогда и только тогда, когда
.На некомпланарных векторах можно построить параллелепипед, объем которого равен .
.
Объем пирамиды равен
Слайд 26Доказательство:
Так как по определению смешанное произведение есть число равное
Слайд 27В результате вычисления данного определителя, находим координаты вектора
Найдем скалярное
произведение векторов и .
Ч.т.д.
Слайд 29
Векторы
называются линейно зависимыми, если найдутся такие действительные числа
, из которых хотя бы одно не равно нулю, а линейная комбинация данных векторов равна нулю.Векторы называются линейно независимыми, если равенство нулю их линейной комбинации возможно лишь в случае, когда все действительные числа равны нулю.
Слайд 30Замечание 1
Если хотя бы один из векторов является нулевым, то
эти векторы линейно зависимы.
Замечание 2
Если среди n векторов любые (n-1)
векторов линейно зависимы, то и все n векторов линейно зависимы.
Слайд 31Теорема 1
Необходимым и достаточным условием линейной зависимости двух векторов является
их коллинеарность.
Следствие 1.
Если два вектора неколлинеарны, то они линейно
независимы.Следствие 2.
Среди двух неколлинеарных векторов не может быть нулевого вектора.
Слайд 32Теорема 2
Необходимым и достаточным условием линейной зависимости трех векторов является
их компланарность.
Следствие 3
Каковы бы не были неколлинеарные векторы
и любой вектор , лежащий с ними в одной плоскости, найдутся такие действительные числа m и n, что 
Слайд 33Теорема 3
Любые четыре вектора линейно зависимы.
Утверждение 1
Любая пара неколлинеарных векторов
на плоскости образует на этой плоскости базис.
Утверждение 2
Любая тройка некомпланарных
векторов образует базис в пространстве. 
