Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциальное исчисление функций одной переменной
Содержание
- 1. Дифференциальное исчисление функций одной переменной
- 2. Основные вопросы:Понятие производной. Геометрический и физический смысл.Понятие сложной функции. Производная сложной функции.Производные высших порядков.
- 3. Предел отношения приращения функции
- 4. Операция вычисления производной называется дифференци-рованием.Функция называется дифференци-руемой
- 5. Касательная и секущая к графику функции. Геометрический и физический смысл производной.
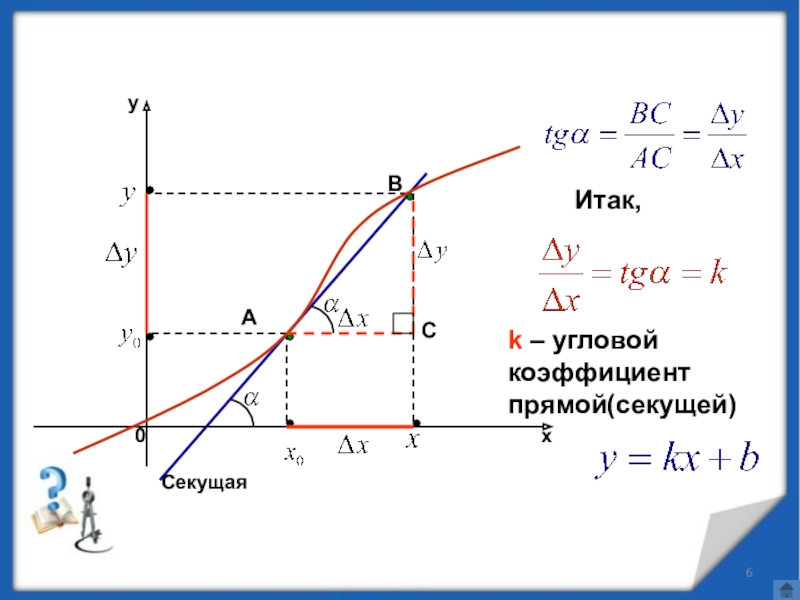
- 6. AB СекущаяСИтак,k – угловой коэффициент прямой(секущей)
- 7. Геометрический смысл отношения при
- 8. Слайд 8
- 9. Алгоритм составления уравнения касательной к графику функции
- 10. Ключевая задача 1. Составьте уравнение касательной
- 11. Задача 2 . Составьте уравнение касательной к
- 12. Если материальная точка движется прямолинейно и ее
- 13. Точка движется прямолинейно по закону
- 14. Найдите скорость и ускорение для точки, движущейся
- 15. 1. Производная от числа (константы) равна нулю.
- 16. 2. Производная переменной равна единице.
- 17. 3. Производная алгебраической суммы (разности) функций равна алгебраической сумме производных этих функций:
- 18. 4. Производная произведения 2-х функций равна сумме произведений каждой из этих функций на производную другой:
- 19. 5. Производная частного 2-х функций равна дроби,
- 20. 6. Постоянный множитель C можно выносить из-под знака производной:
- 21. Функция, заданная формулой
- 22. 7. Производная степенной функции равна произведению показателя степени на переменную в степени меньшей на единицу
- 23. Найдите производную функции:Правильный ответ:
- 24. Найдите производную функции:Правильный ответ:
- 25. Найдите производную функции:Правильный ответ:
- 26. Найдите производную функции:Правильный ответ:
- 27. Производная показательной функцииПоказательная функциядифференцируема в каждой точке
- 28. Производные некоторых элементарных функций.=
- 29. Задание 1.Задание 2.
- 30. Задание 3.Задание 4.
- 31. Задание 5Задание 6
- 32. Задание 7Задание 8
- 33. Таблица производных элементарных функций(С)´= 0, C =
- 34. Сложная функция: Примеры:Правило нахождения производной сложной функции(производная сложной функции равна производной основной функциина производную внутренней функции)
- 35. Сложная функция: Правило нахождения производной сложной функции(производная
- 36. Сложная функция: Правило нахождения производной сложной функции(производная
- 37. Сложная функция: Правило нахождения производной сложной функции(производная сложной функции равна производной основной функциина производную внутренней функции)Пример:
- 38. Сложная функция: Правило нахождения производной сложной функции(производная сложной функции равна производной основной функциина производную внутренней функции)Пример:
- 39. Слайд 39
- 40. Таблица производных для сложной функции
- 41. Производные высших порядков
- 42. Домашнее задание:Колесов В.В. Математика для медицинских колледжей:
- 43. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Дифференциальное исчисление функций одной переменной
РАЗДЕЛ 2. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Тема
2.1. Производная функции. Дифференциал и его приложение к приближенным вычислениям
Слайд 2Основные вопросы:
Понятие производной. Геометрический и физический смысл.
Понятие сложной функции. Производная
сложной функции.
Производные высших порядков.
Слайд 3Предел отношения приращения функции к приращению аргумента
при условии, что - называется производной
данной функции и имеет вид:Определение.
Слайд 4Операция вычисления производной называется дифференци-рованием.
Функция называется дифференци-руемой в данной точке,
если в этой точке существует её производная.
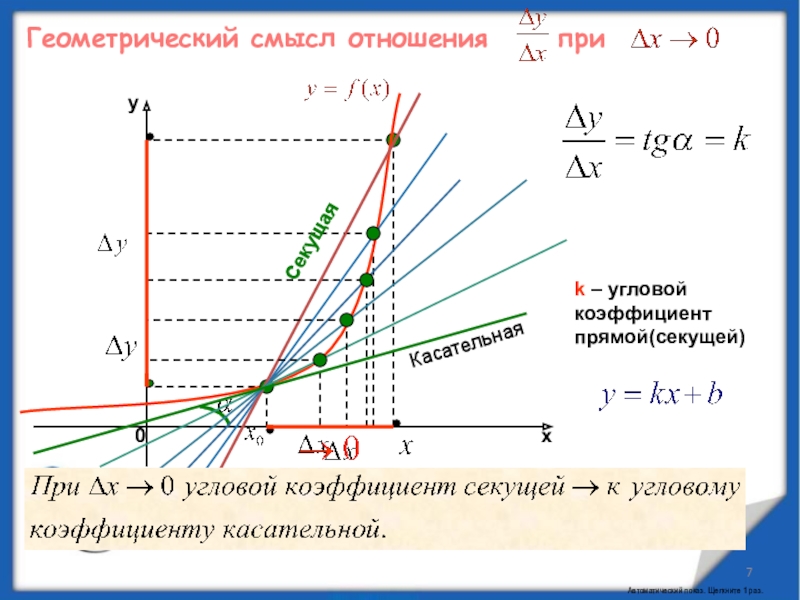
Слайд 7Геометрический смысл отношения при
k – угловой коэффициент прямой(секущей)
Секущая стремится занять
положение касательной. То есть, касательная есть предельное положение секущей.Секущая
Автоматический показ. Щелкните 1 раз.
Слайд 8
k –
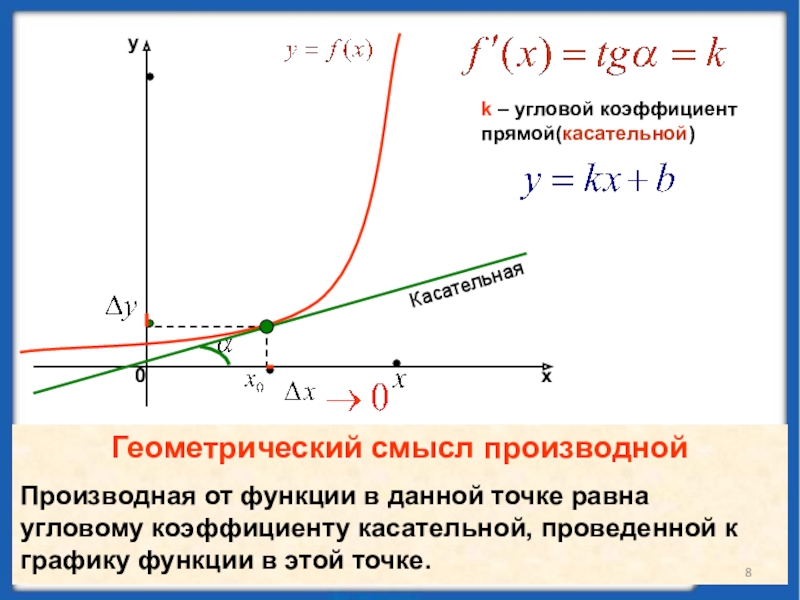
угловой коэффициент прямой(касательной)
Касательная
Геометрический смысл производной
Производная от функции в данной точке
равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.Слайд 9Алгоритм составления уравнения касательной к графику функции y = f(x)
1. Обозначить буквой a абсциссу точки касания.
2. Найти f(a).
3. Найти f '(x) и f '(a).
4. Подставить
найденные числа a, f(a), f '(a) в общее уравнение касательной y = f(a) + f '(a)(x – a).
Слайд 10 Ключевая задача 1. Составьте уравнение касательной к графику функции
у=х2–2х–3 в точке с абсциссой х0=2.
Решение. 1. Обозначим абсциссу точки
касания а, тогда а=2.2. Найдем f(a): f(a)=22–2·2–3, f(a)=-3.
3. Найдем f’ (x) и f’(a): f’(x)=2x–2, f’(a)=2.
4. Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x–a): у=-3+2(х–2),
у=-3+2х–4, у=2х–7 – уравнение касательной.
Ответ: у = 2х –7.
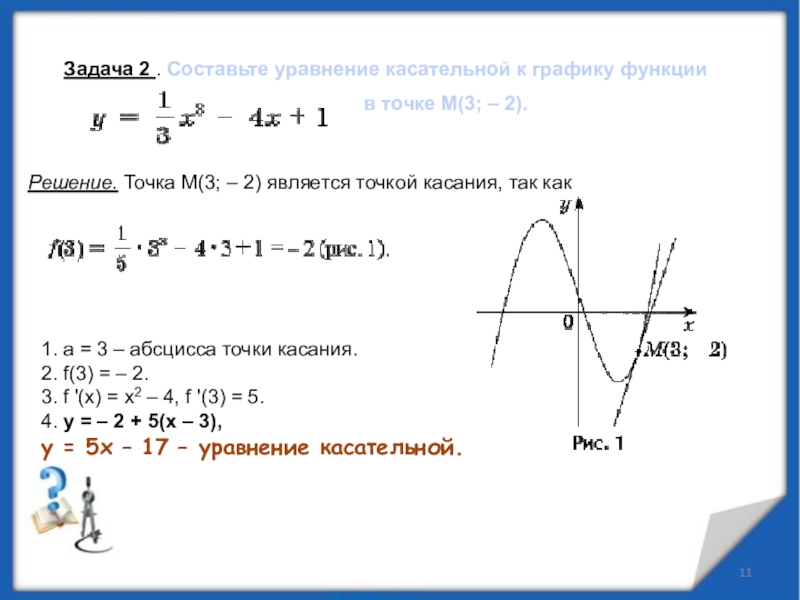
Слайд 11Задача 2 . Составьте уравнение касательной к графику функции
в точке M(3; – 2).
Решение. Точка M(3; – 2) является
точкой касания, так как1. a = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f '(x) = x2 – 4, f '(3) = 5.
4. y = – 2 + 5(x – 3),
y = 5x – 17 – уравнение касательной.
Слайд 12
Если материальная точка движется прямолинейно и ее координата изменяется по
закону x(t), то скорость ее движения v(t) в момент времени
t равна производной т.е. производная от координаты по времени есть скоростьПроизводная от скорости по времени есть ускорение:
Ускорение движения есть скорость изменения скорости, поэтому ускорение движения в момент времени t равно производной
Физический смысл производной функции в данной точке
Слайд 13
Точка движется прямолинейно по закону
Вычислите скорость
движения точки:
а) в момент времени t;
б) в момент времени t=2с.
Решение.
а)
б)
Задача 1
Слайд 14
Найдите скорость и ускорение для точки, движущейся по закону
а) в
момент времени t;
б) в момент времени t=3с.
Решение.
Задача 2
Слайд 173. Производная алгебраической суммы (разности) функций равна алгебраической сумме производных
этих функций:
Слайд 184. Производная произведения 2-х функций равна сумме произведений каждой из
этих функций на производную другой:
Слайд 195. Производная частного 2-х функций равна дроби, числитель которой есть
разность произведений знаменателя на производную числителя и числителя на производную
знаменателя, а знаменатель есть квадрат прежнего знаменателя:Слайд 227. Производная степенной функции равна произведению показателя степени на переменную
в степени меньшей на единицу
Слайд 27Производная показательной функции
Показательная функция
дифференцируема в каждой точке области определения, и
Функция
дифференцируема в каждой точке области определения, и Слайд 33Таблица производных элементарных функций
(С)´= 0, C = const;
(x)´ =
x-1, R, x > 0; (xn)´ = n xn-1, nN,
xR;(ax)´ = axlna, a > 0, a ≠ 1, xR; (ex)´ = ex, xR;
.
(sin x)= cos x, x R;
(cos x) = - sin x, x R;
(tg x) = 1/ cos2x, х ≠ π/2 + πn, n Z;
(ctg x) = - 1/ sin2x, х ≠ πn, n Z;
9)
10)
11)
12)
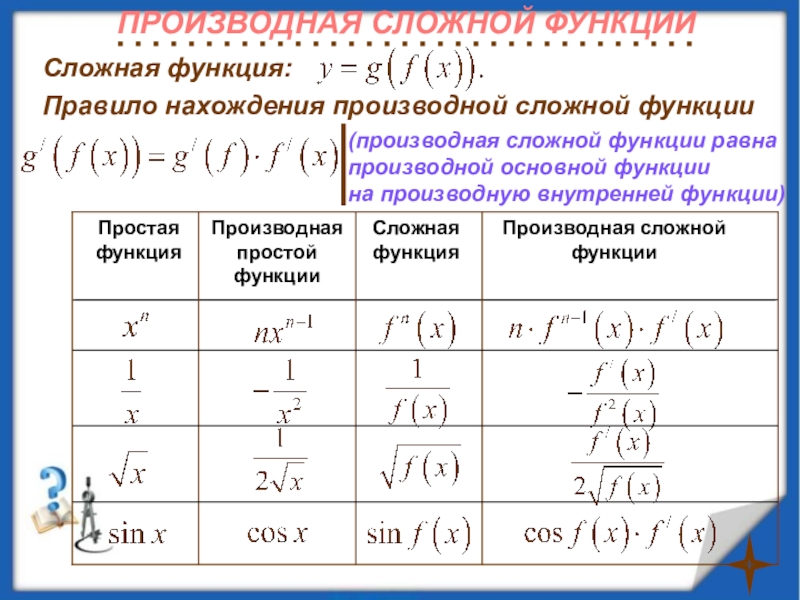
Слайд 34Сложная функция:
Примеры:
Правило нахождения производной сложной функции
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Слайд 35Сложная функция:
Правило нахождения производной сложной функции
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Производная сложной функции
Сложная функция
Производная простой
функцииПростая функция
Слайд 36Сложная функция:
Правило нахождения производной сложной функции
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Производная сложной функции
Сложная функция
Производная простой
функцииПростая функция
Пример:
Слайд 37Сложная функция:
Правило нахождения производной сложной функции
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Пример:
Слайд 38Сложная функция:
Правило нахождения производной сложной функции
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Пример:
Слайд 42Домашнее задание:
Колесов В.В. Математика для медицинских колледжей: учебное пособие/В.В.Колесов, М.Н.
Романов. – Ростов н/Д: Феникс, 2015 – 316 с.: ил.-
(среднее медицинское образование). Гл.7, §7.1 – 7.7Используя материал презентации Занятие 3_Дифференциальное исчисление, выполните из РАБОЧЕЙ ТЕТРАДИ, ТЕМА 2.1, Занятие 3. Дифференциальное исчисление функции одной переменной