Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамическое программирование
Содержание
- 1. Динамическое программирование
- 2. 24.02.2014Динамическое программированиеДинамическое программированиеПример 1: путь минимальной стоимости в слоистой сети (дорог)
- 3. 24.02.2014Динамическое программированиеПусть fn(s) – стоимость пути от
- 4. 24.02.2014Динамическое программирование2-й слойf2(5)= min { C5,8+f1(8) ,
- 5. 24.02.2014Динамическое программирование3-й слойf3(2)= min { C2,5+f2(5) ,
- 6. 24.02.2014Динамическое программирование4-й слой (последний)f4(1) = min {
- 7. 24.02.2014Динамическое программированиеВ общем случаеi – 1 i
- 8. 24.02.2014Динамическое программированиеОсновные особенности метода ДПРекуррентное соотношениеХранение таблицПринцип
- 9. 24.02.2014Динамическое программированиеРешение методом ветвей и границначало324567567576
- 10. 24.02.2014Динамическое программированиеРешение методом ветвей и границначало324567567576
- 11. 24.02.2014Динамическое программированиеДинамическое программирование. Пример 2: Задача о
- 12. 24.02.2014Динамическое программированиеЗадача о порядке перемножения матрицОбщее количество
- 13. 24.02.2014Динамическое программированиеПример: M1 × M2 × M3 × M4, где размер (M1) =
- 14. 24.02.2014Динамическое программированиеРекуррентное соотношениеПусть mij – оптимальное количество
- 15. 24.02.2014Динамическое программирование1) Заметим, что в правой части
- 16. 24.02.2014Динамическое программированиеВ ячейках таблицы T(i, j) хранятся вычисленные значения mij и те значениея qij = k в диапазоне i ≤ k
- 17. 24.02.2014Динамическое программированиеАлгоритм вычисляет оптимальное значение m1n и
- 18. for (i = 1; i < n; i++) m[i][i] = 0;
- 19. 24.02.2014Динамическое программированиеХарактеристики алгоритма Алгоритм требует: порядка n
- 20. 24.02.2014Динамическое программированиеПример вычисления M1 × M2 × M3 × M4 (см. слайд 13)Для
- 21. 24.02.2014Динамическое программированиеСтрока таблицы при L= 2m1,3 = Min {m1k + mk +1,3 + r0 × rk × r3 ⏐ k = 1, 2} = =
- 22. 24.02.2014Динамическое программированиеПоследняя строка таблицы (из одной ячейки)
- 23. 24.02.2014Динамическое программированиеВся таблица вычислена и имеет вид (M1 × (M2 × M3)) × M4
- 24. 24.02.2014Динамическое программированиеВ общем случае порядок перемножения матриц
- 25. «Набросок» функции перемножения цепочки матриц:// Псевдокод Matrix MatrixSeqMult ( int i, int j) // i
- 26. 24.02.2014Динамическое программированиеПолезно сравнить решение, полученное методом динамического
- 27. 24.02.2014Динамическое программированиеДерево перебора в методе ветвей и
- 28. 24.02.2014Динамическое программированиеОценка количества узлов дереваОценить количество узлов
- 29. 24.02.2014Динамическое программированиеНачальное условие p1 = 1. Далее p2 = p1 p1 = 1, p3 = p1 p2 + p2 p1 = 2,
- 30. 24.02.2014Динамическое программирование Тогда для чисел Каталана при больших
- 31. 24.02.2014Динамическое программированиеНесколько первых чисел КаталанаСр. Сn –1 и (n3 – n)/3 Например, при n = 10
- 32. Далее в следующую лекцию24.02.2014Динамическое программирование
- 33. Пример 3. Оптимальные деревья поискаРанее при рассмотрении
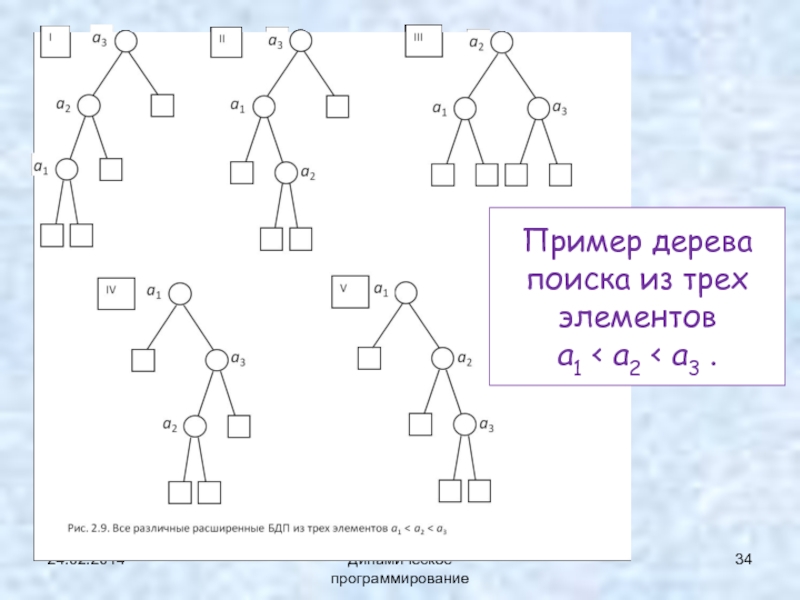
- 34. 24.02.2014Динамическое программированиеПример дерева поиска из трех элементов a1
- 35. Заданы вероятности предъявления элемента x для поиска:
- 36. Постановка задачиПоиск будет осуществляться среди набора данных a1, a2, …, an–1, an. Пусть последовательность упорядочена: a1
- 37. Все эти 2n + 1 событий (исходов поиска) могут быть упорядочены: B0
- 38. Тогда среднее число (математическое ожидание) сравнений при
- 39. Такое дерево называют оптимальным БДП. Есть ли
- 40. НапоминаниеЗадача построения оптимального префиксного кода есть задача
- 41. 24.02.2014Динамическое программированиеИтак, …Есть ли сходство этой задачи
- 42. Очевидное решение поставленной задачи состоит в переборе
- 43. Решение поставленной задачи методом динамического программированияна следующей лекции.24.02.2014Динамическое программирование
- 44. 24.02.2014Динамическое программированиеКОНЕЦ ЛЕКЦИИКОНЕЦ ЛЕКЦИИКОНЕЦ
- 45. Скачать презентанцию
Слайды и текст этой презентации
Слайд 124.02.2014
Динамическое программирование
Построение и анализ алгоритмов
Лекция 3
Динамическое программирование
Слайд 224.02.2014
Динамическое программирование
Динамическое программирование
Пример 1:
путь минимальной стоимости в слоистой сети
(дорог)
Слайд 324.02.2014
Динамическое программирование
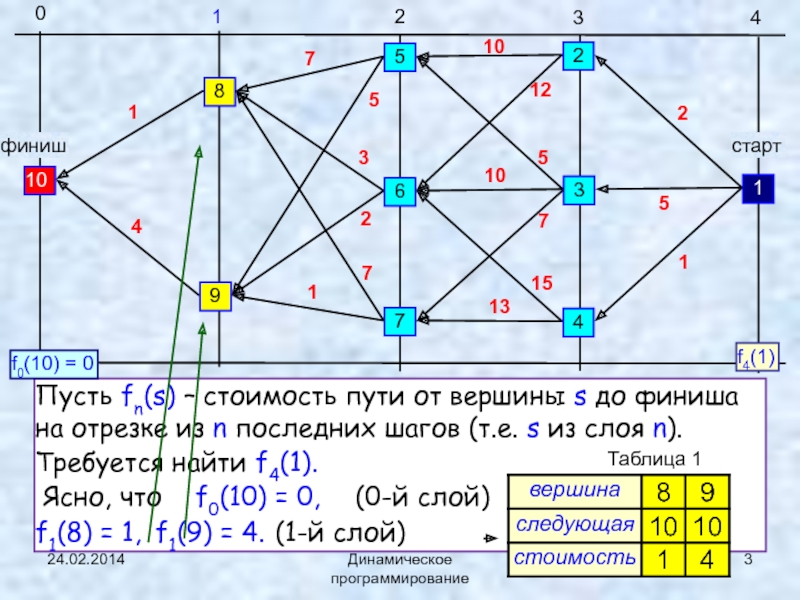
Пусть fn(s) – стоимость пути от вершины s до
финиша на отрезке из n последних шагов (т.е. s из
слоя n).Требуется найти f4(1).
Ясно, что f0(10) = 0, (0-й слой)
f1(8) = 1, f1(9) = 4. (1-й слой)
Таблица 1
f0(10) = 0
f4(1)
Слайд 424.02.2014
Динамическое программирование
2-й слой
f2(5)= min { C5,8+f1(8) , C5,9+f1(9) } =
min {7+1, 5+4} = 8.
f2(6)= min { C6,8+f1(8) , C6,9+f1(9)
} = min {3+1, 2+4} = 4.f2(7)= min { C7,8+f1(8) , C7,9+f1(9) } = min {7+1, 1+4} = 5.
Таблица 2
Слайд 524.02.2014
Динамическое программирование
3-й слой
f3(2)= min { C2,5+f2(5) , C2,6+f2(6) } =
min {10+8, 12+4} = 16.
f3(4)= min { C4,6+f2(6) , C4,7+f2(7)
} = min {15+8, 13+5} = 18.Таблица 3
f3(3)= min { C3,5+f2(5) , C3,6+f2(6), C3,7+f2(7) } =
= min { 5+8, 10+4, 7+5 } = 12.
Слайд 624.02.2014
Динамическое программирование
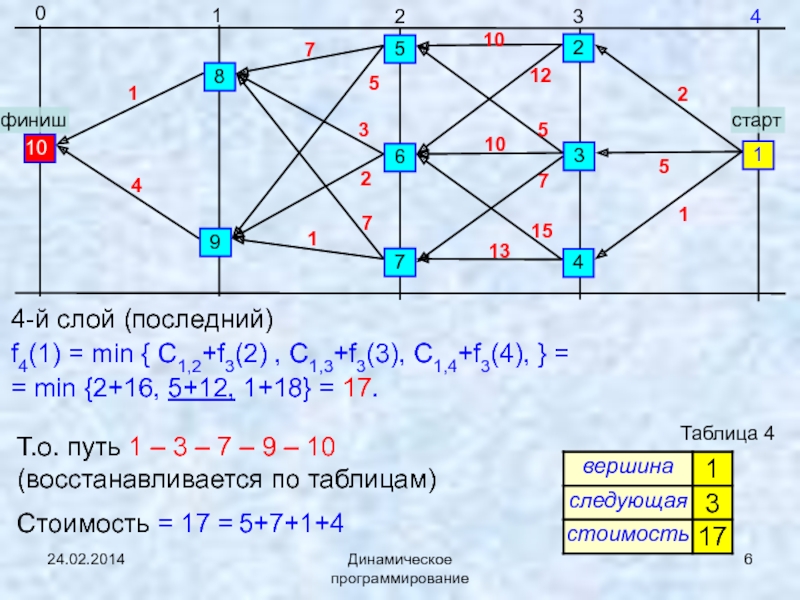
4-й слой (последний)
f4(1) = min { C1,2+f3(2) , C1,3+f3(3),
C1,4+f3(4), } =
= min {2+16, 5+12, 1+18} = 17.
Таблица
4Т.о. путь 1 – 3 – 7 – 9 – 10 (восстанавливается по таблицам)
Стоимость = 17 = 5+7+1+4
Слайд 724.02.2014
Динамическое программирование
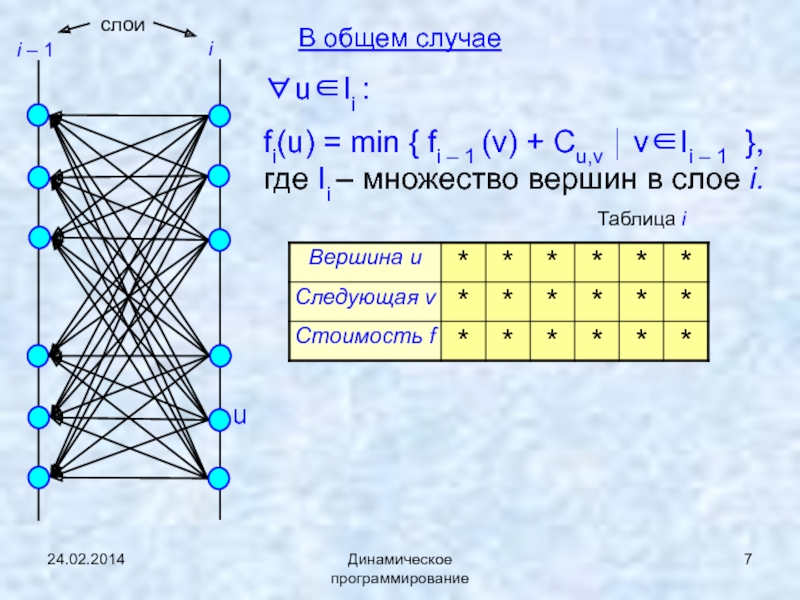
В общем случае
i – 1
i
слои
∀u∈Ii :
fi(u)
= min { fi – 1 (v) + Cu,v ⏐
v∈Ii – 1 }, где Ii – множество вершин в слое i.u
Таблица i
Слайд 824.02.2014
Динамическое программирование
Основные особенности метода ДП
Рекуррентное соотношение
Хранение таблиц
Принцип оптимальности:
Часть (например,
f i – 1 (v)) оптимального решения fi(u) должна быть
оптимальнаfi(u) = min { f i – 1 (v) + Cu,v⏐ v∈Ii – 1 }, i∈1..n, f0(u)=0
Слайд 1124.02.2014
Динамическое программирование
Динамическое программирование.
Пример 2: Задача о порядке перемножения матриц
Рассмотрим произведение
матриц M1 × M2 × M3 × ... × Mn −1 × Mn.
Каждая матрица Mi имеет размер ri −1 × ri.
M1 (r0;r1)×M2(r1;r2)×M3(r2;r3)×...×Mn −1(rn −
2;rn − 1)×Mn (rn − 1;rn). Вычисление произведения двух матриц –
размер первой n × p и размер второй p × m –
требует n p m умножений их элементов:
C (n;m) = A(n;p) × B(p;m)
cij = Σk=1..p (aik * bkj ) для i ∈1..n, j ∈1..m
Слайд 1224.02.2014
Динамическое программирование
Задача о порядке перемножения матриц
Общее количество элементарных операций умножения,
требуемое при вычислении произведения цепочки матриц, зависит от порядка, в
котором производятся попарные умножения матриц.Требуется найти такой порядок перемножения матриц, который минимизирует общее количество элементарных операций умножения.
Слайд 1324.02.2014
Динамическое программирование
Пример: M1 × M2 × M3 × M4,
где размер (M1) = 10 × 20,
размер (M2)
= 20 × 50,
размер (M3) = 50 × 1,
размер (M3) = 1 × 100.
M1 × M2 × M3 × M4,
M1
M2
M3
M4
1) M1 × (M2 × (M3 × M4)) ⇒ (10×20×100 (20×50×100 (50×1×100) ) ) ⇒ 125 000
20 000
100 000
5 000
2) (M1 × (M2 × M3)) × M4 ⇒ ( (10×20×1 (20×50×1) ) 10×1×100 ) ⇒ 2 200
1 000
200
1 000
Слайд 1424.02.2014
Динамическое программирование
Рекуррентное соотношение
Пусть mij – оптимальное количество умножений, требуемое для
вычисления произведения цепочки матриц M(i, j) = Mi × Mi +1 × ... × Mj −1 × Mj,
где 1≤ i ≤ j ≤ n.
Очевидно, что M(i, i) = Mi
и mii = 0, а m1n – соответствует решению задачи для исходной цепочки M(1, n).
При 1≤ i < j ≤ n справедливо :
mij = Min {mik + mk +1, j + ri − 1 × rk × rj ⏐ i ≤ k < j}.
M(i, j) = M(i, k) × M(k+1, j), i ≤ k < j
ri − 1 × rj ri − 1 × rk rk × rj
Слайд 1524.02.2014
Динамическое программирование
1) Заметим, что в правой части равенства разности индексов
k – i и j – k –1 у слагаемых mik и mk +1, j меньше, чем разность индексов j – i в
mij.Таким образом, рекуррентное соотношение следует решать, начиная с mii = 0 и последовательно увеличивая разность индексов j – i до тех пор, пока не получим m1n.
2) Удобно представлять результаты вычислений в виде таблицы.
В этой таблице строка с номером l состоит из ячеек T(i, j), индексы которых связаны соотношением j – i = l.
Т.е. j = i + l и T(i, j) = T(i, i + l).
Слайд 1624.02.2014
Динамическое программирование
В ячейках таблицы T(i, j) хранятся вычисленные значения mij и
те значениея qij = k в диапазоне i ≤ k
Min { mik + mk +1, j + ri −1 × rk × rj }.Слайд 1724.02.2014
Динамическое программирование
Алгоритм вычисляет оптимальное значение m1n и заполняет
таблицу T
по строкам сверху вниз:
for (i = 1; i < n; i++)
m[i, i] = 0; //заполнение первой строкиfor l := 1 to n –1 do
for i := 1 to n – l do
begin
j := i + l;
{заполнение T(i, j):}
m[i, j] := +∞;
for k := i to j – 1 do
begin
s := m[i, k] + m [k +1,j] + ri −1 * rk * rj;
if s < m[i, j] then
begin m[i, j] := s;
q[i, j] := k
end { if }
end { for k }
end { for i }
Слайд 18 for (i = 1; i < n; i++) m[i][i] = 0; //заполнение первой строки
табл.
for (L = 1; L < n; L++)
for (i = 1; i
n-L+1; i++) {j = i + L;
// заполнение T(i, j):
m[i][j] = +∞;
for (k = i; k < j; k++) {
s = m[i][k] + m[k+1][j] + r(i-1) * r(k) * r(j);
if (s < m[i][j]){
m[i][j] = s;
q[i][j] = k;
}
}
}
24.02.2014
Динамическое программирование
Алгоритм вычисляет оптимальное значение m1n и заполняет
таблицу T по строкам сверху вниз:
Слайд 1924.02.2014
Динамическое программирование
Характеристики алгоритма
Алгоритм требует:
порядка n 2/2 элементов памяти
для хранения таблицы
около n 3/3 выполнений тела внутреннего цикла.
Пример см. далее
Слайд 2024.02.2014
Динамическое программирование
Пример вычисления M1 × M2 × M3 × M4 (см. слайд 13)
Для заполнения строки таблицы
при l = 1 вычислим последовательно
m1,2 = m1,1 + m2,2 + r0 × r1 × r2 = 10 × 20 × 50 = 10 000,
m2,3 = m2,2 + m3,3 + r1 × r2 × r3 = 20 × 50 × 1 = 1000,
m3,4 = m3,3 + m4,4 + r2 × r3 × r4 = 50 × 1 × 100 = 5000.
Здесь фактически минимум находить не требуется, так как тело цикла по k выполняется лишь один раз (при k = i ). Заполненная строка таблицы есть
mij = Min {mik + mk +1, j + ri − 1 × rk × rj ⏐ i ≤ k < j}.
Слайд 2124.02.2014
Динамическое программирование
Строка таблицы при L= 2
m1,3 = Min {m1k + mk +1,3 + r0 × rk × r3 ⏐ k = 1, 2} =
= Min {m1,1 + m2,3 + r0 × r1 × r3 , m1,2 + m3,3 + r0 × r2 × r3} =
=
Min {0 + 1000 + 200, 10 000 + 0 + 500} =
= Min{1200, 10 500} = 1200 (при k = 1),
m2,4 = Min {m2k + mk +1,4 + r1× rk × r4⏐ k = 2, 3} =
= Min {m2,2 + m3,4 + r1 × r2 × r4 , m2,3 + m4,4 + r0 × r2 × r3} =
= Min
{0 + 5000 + 100 000, 1000 + 0 + 2000} == Min{105 000, 3000} = 3000 (при k = 3)
mij = Min {mik + mk +1, j + ri − 1 × rk × rj ⏐ i ≤ k < j}.
Слайд 2224.02.2014
Динамическое программирование
Последняя строка таблицы
(из одной ячейки) Т (1, 4):
m1,4 = Min {
m1k + mk +1,4 + r0 × rk × r4 ⏐ k = 1, 2, 3} =
= Min { m1,1 + m2,4 + r0 × r1 × r4,
m1,2 + m3,4 + r0 × r2 × r4, m1,3 + m4,4 + r0 × r3 × r4 } =
= Min {0 + 3000 + 20 000,
10 000 + 5000 + 50 000,
1200 + 0 + 1000} =
= Min {23 000, 65 000, 2200} = 2200 (при k = 3).
mij = Min {mik + mk +1, j + ri − 1 × rk × rj ⏐ i ≤ k < j}.
Слайд 2324.02.2014
Динамическое программирование
Вся таблица вычислена и имеет вид
(M1 × (M2 × M3)) × M4
Слайд 2424.02.2014
Динамическое программирование
В общем случае порядок перемножения матриц легко определить рекурсивно.
Пусть имеется функция перемножения двух матриц func Mult ( A, B: Matrix): Matrix. «Набросок» функции перемножения
цепочки матриц:func MatrixSeqMult ( i, j: Index): Matrix; {i ≤ j}
global q: Tab_q;
var k: Index; var A, B: Matrix;
begin
if i < j then
begin
k := q[i, j];
A := MatrixSeqMult ( i, k);
B := MatrixSeqMult ( k +1, j);
Return Mult(A, B)
end
else {i = j} Return Mi
end {MatrixSeqMult}
Слайд 25«Набросок» функции перемножения цепочки матриц:
// Псевдокод
Matrix MatrixSeqMult ( int i, int j) //
i
{k = q[i][j];
A = MatrixSeqMult ( i, k);
B = MatrixSeqMult ( k +1, j);
return Mult(A, B);
}
else // i = j
return M[i]
}
24.02.2014
Динамическое программирование
Слайд 2624.02.2014
Динамическое программирование
Полезно сравнить решение, полученное методом динамического программирования, с решением
методом ветвей и границ.
В рассмотренном примере возможны следующие 5
вариантов перемножения матриц M1 × M2 × M3 × M4, а именно:M1 × (M2 × (M3 × M4)),
M1 × ((M2 × M3) × M4),
(M1 × M2) × (M3 × M4),
(M1 × (M2 × M3)) × M4,
((M1 × M2) × M3) × M4.
Слайд 2724.02.2014
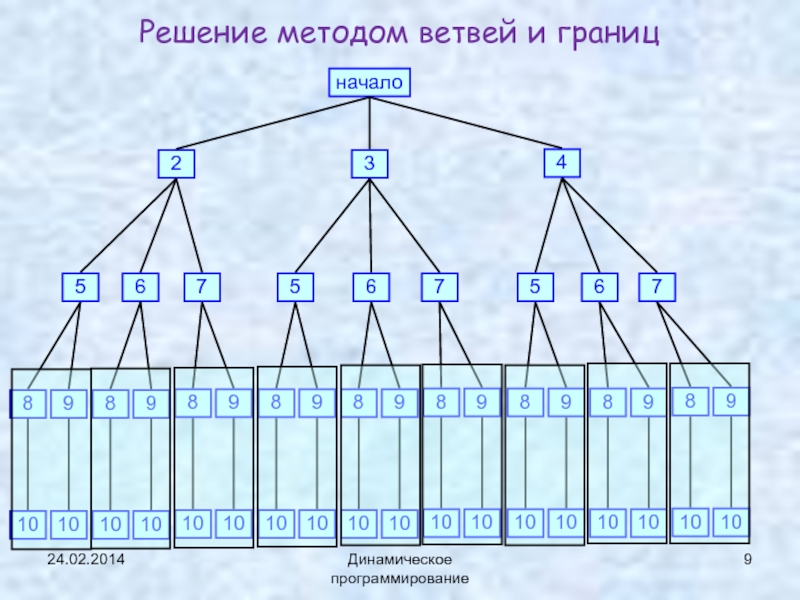
Динамическое программирование
Дерево перебора в методе ветвей и границ
M(1,4)
M1 × M(2,4)
M(1,2) × M(3,4)
M(1,3) × M4M2 × M(3,4) M(2,3) × M4 M1 × M2 M3 × M4 M1 × M(2,3) M(1,2) × M3
M3 × M4 M2 × M3 M2 × M3 M1 × M2
В методе динамического программирования повторных вычислений
не делается.
Вычисления проводятся так, как будто дерево сканируется снизу вверх,
а результаты вычислений сохраняются в таблице и далее используются.
Слайд 2824.02.2014
Динамическое программирование
Оценка количества узлов дерева
Оценить количество узлов дерева в общем
случае можно подсчетом всех возможных вариантов расстановок скобок в произведении
матриц.Пусть pn – число вариантов расстановок скобок в произведении n сомножителей (включая самые внешние скобки).
Например, для трех сомножителей abc имеем два варианта (a(bc)) и ((ab)c), а следовательно, p3 = 2.
В общем случае, считая, что «последнее» по порядку умножение может оказаться на любом из n –1 мест, запишем следующее рекуррентное соотношение:
pn = p1 pn –1 + p2 pn –2 + … + pn –2 p2 + p n –1 p1.
Слайд 2924.02.2014
Динамическое программирование
Начальное условие p1 = 1. Далее
p2 = p1 p1 = 1,
p3 = p1 p2 + p2 p1 = 2,
p4 = p1 p3 + p2 p2 + p3 p1 = 5.
Оказывается [7,
с. 393], что решением этого рекуррентного уравнения являются так называемые
числа
Каталана pn = Сn –1, где Сk =(2 k | k) / (k +1),
а запись (n | m) обозначает биномиальный коэффициент (n | m) = n !/(m ! (n – m)!).
См. также 1.6.10 и 1.7.4 в книге
Слайд 3024.02.2014
Динамическое программирование
Тогда для чисел Каталана при больших значениях n справедливо
т. е. число узлов в дереве перебора есть
экспоненциальная функция от
n. При больших значениях k удобно использовать
формулу Стирлинга
Слайд 3124.02.2014
Динамическое программирование
Несколько первых чисел Каталана
Ср. Сn –1 и (n3 – n)/3
Например, при n = 10
Слайд 33Пример 3.
Оптимальные деревья поиска
Ранее при рассмотрении БДП, как правило, предполагалось,
что для поиска различные ключи предъявляются с равной вероятностью.
Пусть теперь
заранее известно, что некоторые ключи предъявляются чаще других. Тогда расположение «частых» ключей ближе к корню дерева сократит время их поиска и, возможно, среднее время поиска (по разным предъявлениям ключей).
24.02.2014
Динамическое программирование
Слайд 35Заданы вероятности предъявления элемента x для поиска: P (x = a1) = α; P
(x = a2) = β; P (x = a3) = γ.
24.02.2014
Динамическое программирование
Среднее (по всем предъявлениям x) число
сравнений (стоимость) в случаях успешного поиска как функция переменных α, β и γ, Слайд 36Постановка задачи
Поиск будет осуществляться среди набора данных a1, a2, …, an–1, an.
Пусть последовательность
упорядочена:
a1
Ai : (x = ai) для i ∈ 1..n, B0, …, Bn - события, соответствующие вариантам неудачных исходов поиска,
т. е. Bi : (ai < x < ai+1) для i ∈ 0..n.
Здесь для упрощения записи событий B0 и Bn добавлены фиктивные элементы a0 = −∞ и an+1 = +∞, которые не должны использоваться в алгоритме.
24.02.2014
Динамическое программирование
Слайд 37Все эти 2n + 1 событий (исходов поиска)
могут быть
упорядочены:
B0
i ∈ 1..n, и qi = P (Bi) для i ∈ 0..n. При этом Σi∈1..n pi + Σi∈0..n qi = 1.
События Ai соответствуют внутренним узлам расширенного дерева поиска, а события Bi – внешним узлам (листьям) расширенного дерева поиска.
24.02.2014
Динамическое программирование
Постановка задачи (продолжение)
Слайд 38Тогда среднее число (математическое ожидание) сравнений при поиске можно записать
в виде
где l (x) – уровень узла x (или длина
пути от корня до узла x) в БДП. Здесь уровень узла определен так, что l (корень) = 0.
24.02.2014
Динамическое программирование
Постановка задачи (продолжение)
Итак, задача состоит в том, чтобы по заданным весам
построить БДП, минимизирующее значение C0,n .
Слайд 39Такое дерево называют оптимальным БДП.
Есть ли сходство этой задачи
с задачей построения оптимального префиксного кода ?
24.02.2014
Динамическое программирование
Постановка задачи (продолжение)
Слайд 40Напоминание
Задача
построения оптимального префиксного кода есть задача минимизации функции
L = Σi
=1..n wi li
целочисленных положительных переменных (li)1n при заданном наборе (wi)1n
и
при условии (здесь не формализованном) выполнения свойства префиксности кода. Набор переменных (li)1n, минимизирующий L, определяет структуру дерева (кода).
24.02.2014
Динамическое программирование
Слайд 41
24.02.2014
Динамическое программирование
Итак, …
Есть ли сходство этой задачи с задачей построения
оптимального префиксного кода ?
В чём сходство, в чём различие?
Ответ.
Слайд 42Очевидное решение поставленной задачи состоит в переборе всех структурно различных
бинарных деревьев с n узлами и выборе дерева с наименьшей
стоимостью C0,n .Однако поскольку (см. лекции про БДП) число bn структурно различных бинарных деревьев с n узлами есть
, то этот способ вряд ли будет иметь практическую ценность.
Оказывается, приемлемое по количеству вычислений решение данной задачи может быть получено методом динамического программирования.
24.02.2014
Динамическое программирование













![Динамическое программирование for (i = 1; i < n; i++) m[i][i] = 0; //заполнение первой строки табл. for for (i = 1; i < n; i++) m[i][i] = 0; //заполнение первой строки табл. for (L = 1; L < n; L++) for](/img/thumbs/35a6a3918b993fbc8eb09534ce1b2ead-800x.jpg)










![Динамическое программирование 24.02.2014Динамическое программированиеНачальное условие p1 = 1. Далее p2 = p1 p1 = 1, p3 = p1 p2 + p2 p1 = 2, p4 = p1 p3 + p2 p2 + p3 p1 = 5. Оказывается [7, с. 393], 24.02.2014Динамическое программированиеНачальное условие p1 = 1. Далее p2 = p1 p1 = 1, p3 = p1 p2 + p2 p1 = 2, p4 = p1 p3 + p2 p2 + p3 p1 = 5. Оказывается [7, с. 393], что решением этого рекуррентного уравнения являются](/img/tmb/2/153225/7390f70dd622c7c565f3dcd451ea3083-800x.jpg)