Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
14.10.2019 Материалы к ШМО МБОУ СОШ №11 пгт.Шерегеш Подготовка к
Содержание
- 1. 14.10.2019 Материалы к ШМО МБОУ СОШ №11 пгт.Шерегеш Подготовка к
- 2. Математика является одним из наиболее важных предметов школьного курса.Статус математики
- 3. Каждый школьник в процессе обучения должен иметь
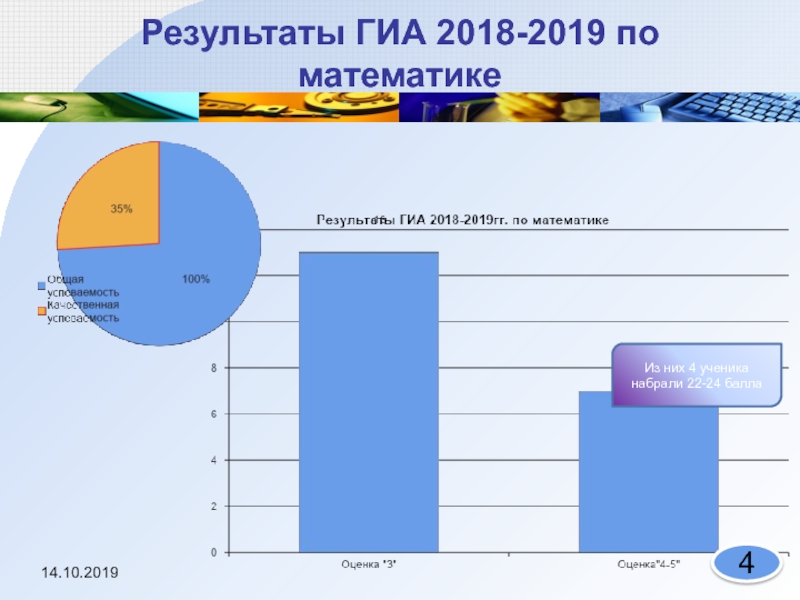
- 4. Результаты ГИА 2018-2019 по математикеИз них 4 ученика набрали 22-24 балла 14.10.2019 4
- 5. «Западающие темы»14.10.2019 Геометрические задачиГрафики функцийТекстовые задачиНеравенстваФормулы сокращенного умножения5
- 6. Цели и задачиЦели:Подготовка учащихся к успешной сдачи
- 7. Краткое описание работы Презентация содержит алгоритмы построения
- 8. Построение графиков функций с выражениями под знаком
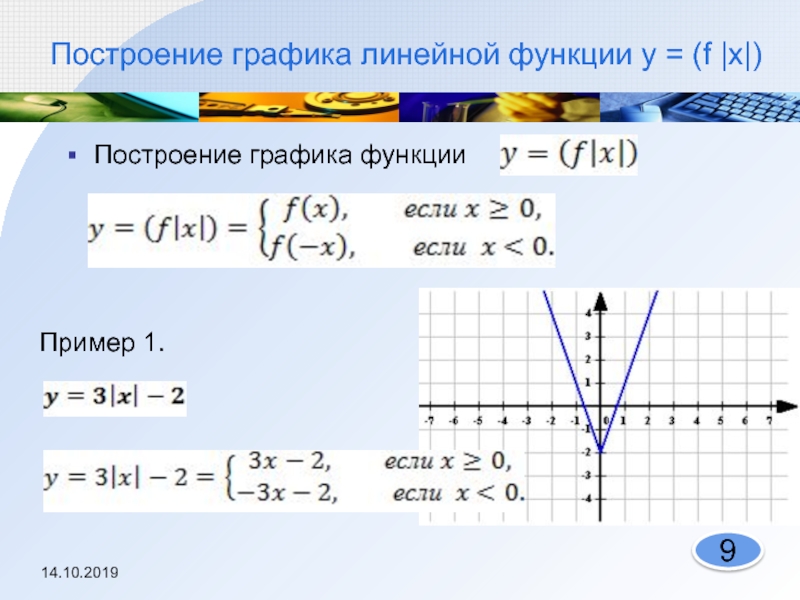
- 9. Построение графика линейной функции y = (f |x|)Построение графика функции 14.10.2019 9Пример 1.
- 10. Построение графика линейной функции y =
- 11. Построение графика линейной функции y = |f
- 12. Пример 3. Построение графика линейной функции y
- 13. Построение графиков функций у = |ах2+bх+с|
- 14. Построение графиков функций у = |ах2+bх+с|
- 15. Пример 4. Построение графика функции у
- 16. Пример 4. Построение графика функции у
- 17. Пример 4. Построение графика функции 4)
- 18. Пример 5. Построение графика функции у
- 19. Алгоритм. Построение графика функции у =
- 20. Построение графика функции у = |ах2+b|х|+с |
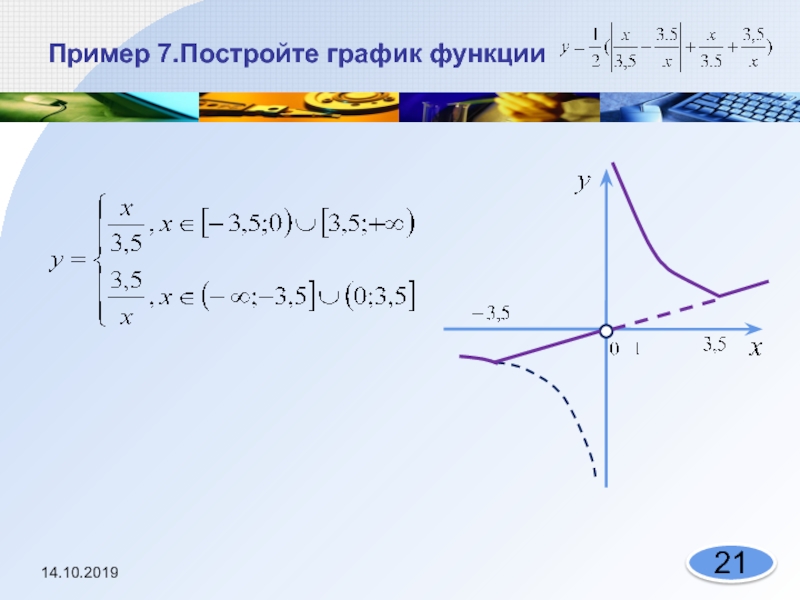
- 21. Пример 7.Постройте график функции-3,5 3,50+--+14.10.2019 20
- 22. Пример 7.Постройте график функции14.10.2019 21
- 23. Использованные материалы и литература:Алгебра.7-9 класс: учеб.для общеобразоват.
- 24. Спасибо за внимание.Всем творческих успехов!!!14.10.2019
- 25. Скачать презентанцию
Математика является одним из наиболее важных предметов школьного курса.Статус математики как обязательного государственного экзамена подтверждает необходимость изучения математики каждым учащимся14.10.20192
Слайды и текст этой презентации
Слайд 114.10.2019
Материалы к ШМО
МБОУ СОШ №11
пгт.Шерегеш
Подготовка к ОГЭ.
Построение
графика функции, содержащей модуль
Слайд 2Математика является одним из наиболее важных предметов школьного курса.
Статус математики как обязательного государственного
экзамена подтверждает
необходимость изучения
математики
каждым учащимся
14.10.2019
2
Слайд 3Каждый школьник в процессе обучения должен иметь возможность получить качественную
подготовку к выпускным экзаменам, освоить тот объём знаний, умений и
навыков, который необходим для успешной сдачи ОГЭ в 9 классе, дальнейшего обучения в 10-11 классах, сдачи ЕГЭ и последующего обучения в вузе.14.10.2019
3
Слайд 5«Западающие темы»
14.10.2019
Геометрические задачи
Графики функций
Текстовые задачи
Неравенства
Формулы сокращенного умножения
5
Слайд 6Цели и задачи
Цели:
Подготовка учащихся к успешной сдачи ОГЭ по математике
Задачи:
Обучить
строить графики функции, содержащей модуль, посредством алгоритмизации шагов;
Углубить знания по
математике, предусматривающие формирование у учащихся устойчивого интереса к предмету;Расширить математические представления учащихся о приёмах и методах решения задач с модулями;
14.10.2019
6
Слайд 7Краткое описание работы
Презентация содержит алгоритмы построения графиков функций, содержащих
модуль, семь примеров построения графиков функции.
14.11.2017
Формат презентации дает
возможность учителю обсудить шаги выполнения задания с обучающимися, дать возможность самим обучающимся выполнить действие, а потом уже проконтролировать, используя анимацию. 7
Слайд 8Построение графиков функций с выражениями под знаком модуля
Построение графиков, содержащих модуль, осуществляется двумя способами:
На основании определения
модуля; На основании правил геометрического преобразования графиков функций.
По определению модуля числа:
14.11.2017
8
Слайд 9Построение графика линейной функции y = (f |x|)
Построение графика функции
14.10.2019
9
Пример 1.
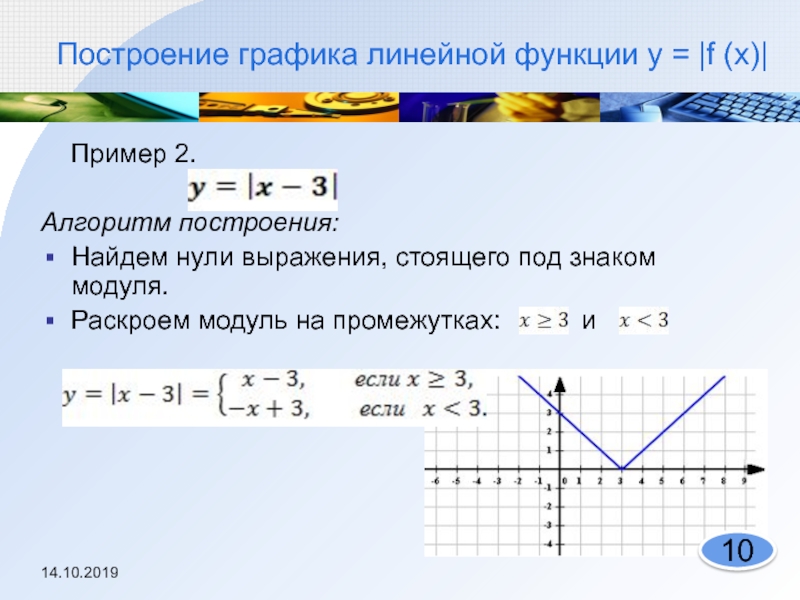
Слайд 10 Построение графика линейной функции y = |f (x)|
Пример 2.
Алгоритм построения:
Найдем нули выражения, стоящего под знаком модуля.
Раскроем модуль
на промежутках: и 14.10.2019
10
Слайд 11Построение графика линейной функции y = |f (x)|
Пример 3.
Построить график
функции
Найдем нули выражений, стоящих под знаком модуля.
Получим три промежутка:
Расставим знаки для подмодульных выражений на координатной прямой:
14.10.2019
11
Слайд 12Пример 3. Построение графика линейной функции y = |f (x)|
Раскроем
знаки модуля на промежутках:
Раскрыв скобки и выполнив тождественные преобразования, получим:
Строим
график:
0 х
-7
14.10.2019
12
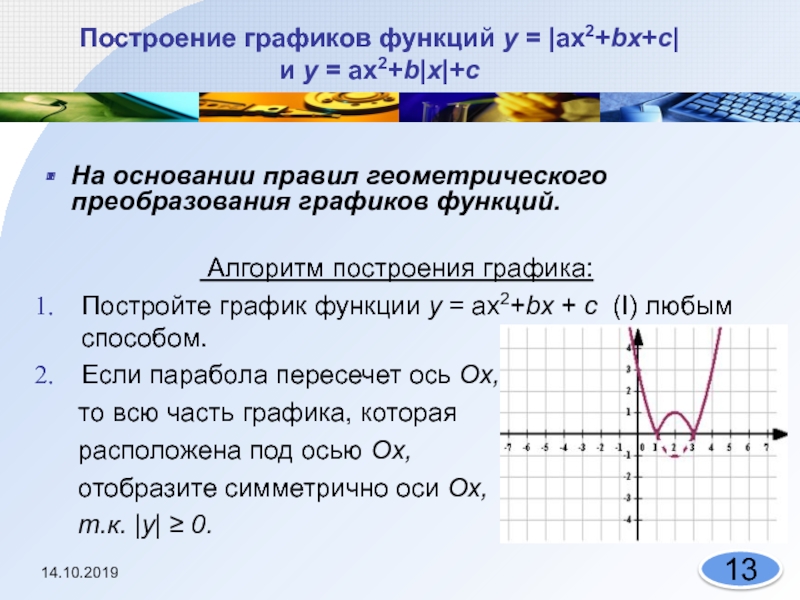
Слайд 13Построение графиков функций у = |ах2+bх+с|
и у = ах2+b|х|+с
На
основании правил геометрического преобразования графиков функций.
Алгоритм построения графика:
Постройте график
функции у = ах2+bх + с (I) любым способом.Если парабола пересечет ось Ох,
то всю часть графика, которая
расположена под осью Ox,
отобразите симметрично оси Ox,
т.к. |y| ≥ 0.
14.10.2019
13
Слайд 14Построение графиков функций у = |ах2+bх+с|
и у = ах2+b|х|+с
3.
Если парабола расположена над осью Ох,
то |ах2+bх+с| = ах2+bх+с
при всех значениях х,а значит, весь график сохранит свое положение.
4. Если вся парабола (I) расположена под осью Ох,
( а < 0; D < 0), то графиком функции у = |ах2+bх+с| будет парабола, расположенная над осью Ох симметрично параболе (I) относительно оси Ох.
5. Если надо построить график функции у = ах2+b|х| + с , то всю часть графика (I), которая справа от оси Оу, отобразите симметрично оси ОУ, а левую часть графика (I) относительно оси ОУ стройте пунктиром.
14.10.2019
14
Слайд 15Пример 4. Построение графика функции
у = |ах2+bх+с|
1)
Постройте график функции
у =ах2+bх+с (I) любым способом.
Построение
1) Найдем координаты вершины параболы:
Подставим в трехчлен и найдем
- вершина параболы
.
-
14.11.2017
15
Слайд 16Пример 4. Построение графика функции
у = |ах2+bх+с|
- ось симметрии;
Точки пересечения с осью
Ох:- точки пересечения с осью Ох.
14.11.2017
16
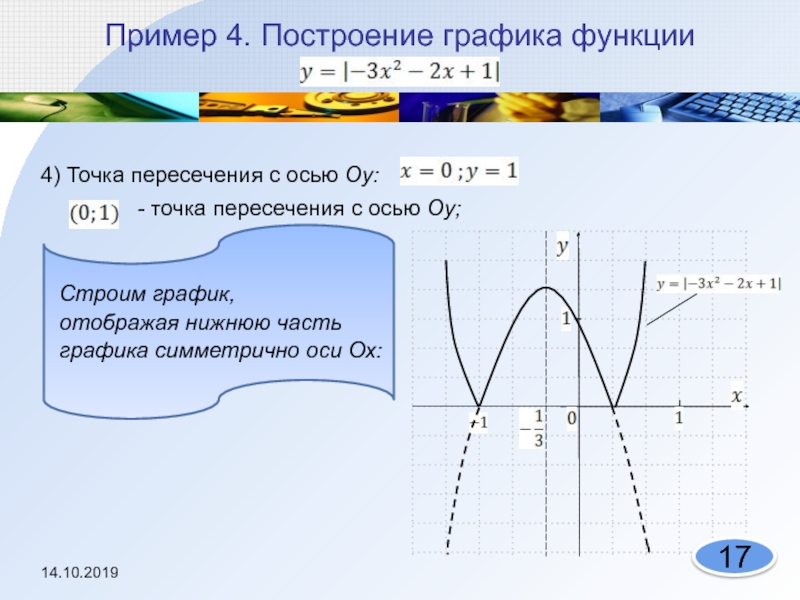
Слайд 17Пример 4. Построение графика функции
4) Точка пересечения с осью
Оу:
- точка пересечения
с осью Оу;Строим график,
отображая нижнюю часть
графика симметрично оси Ох:
14.10.2019
17
Слайд 18Пример 5. Построение графика функции
у = ах2+b|х|+с
Построим график
функции
:Найдем координаты вершины параболы:
- вершина параболы
2. - ось симметрии
3. Точки пересечения с осью Ох:
- нет корней, точек пересечения с осью Ох нет
4. Точка пересечения с осью Оу:
- точка пересечения с осью Оу
14.10.2019
18
Слайд 19Алгоритм. Построение графика функции
у = |ах2+b|х|+с|
Постройте график функции у
= ах2+bх+с .
Постройте график функции у = ах2+b|х|+с. Для этого
постройте симметрично оси Оу ту часть графика, которая справа от оси Оу.Постройте симметрично оси Ох ту часть графика, которая находится под осью Ох. Построенный график является графиком функции у = |ах2+b|х|+с|
14.10.2019
18
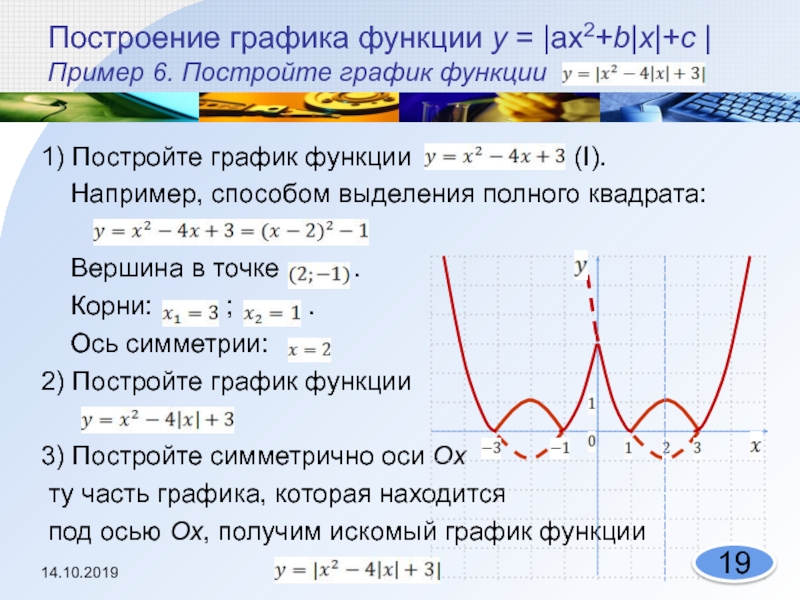
Слайд 20Построение графика функции у = |ах2+b|х|+с | Пример 6. Постройте график
функции
1) Постройте график функции
(I).Например, способом выделения полного квадрата:
Вершина в точке .
Корни: ; .
Ось симметрии:
2) Постройте график функции
3) Постройте симметрично оси Оx
ту часть графика, которая находится
под осью Ох, получим искомый график функции
14.10.2019
19
Слайд 23Использованные материалы и литература:
Алгебра.7-9 класс: учеб.для общеобразоват. организаций/Ю.Н.Макарычев, Н.Г.Миндюк, К.Нешков,С.Б.Суворова;
под ред.С.А.Теляковского.-4-е изд.-М.:Просвещение, 2015
Башмаков М.И. Уравнения и неравенства.
Михайлова Ж.Н.
Алгоритмы - ключ к решению задач: Алгебра. 7-9 классы.-СПб.:Издательский дом «Литера»,2014. ‑ 448 с.: ил..-(Серия «Средняя школа»)http://www.fipi.ru/ http://reshuege.ru/ Сайт Федерального института педагогических измерений (ФИПИ)
14.10.2019
23
