е в о п р о с ы
( в
скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 32» )
1. Каковы основные предпосылки и гипотезы теории динамических расчётов
линейно деформируемых систем с распределёнными массами? ( 2 )
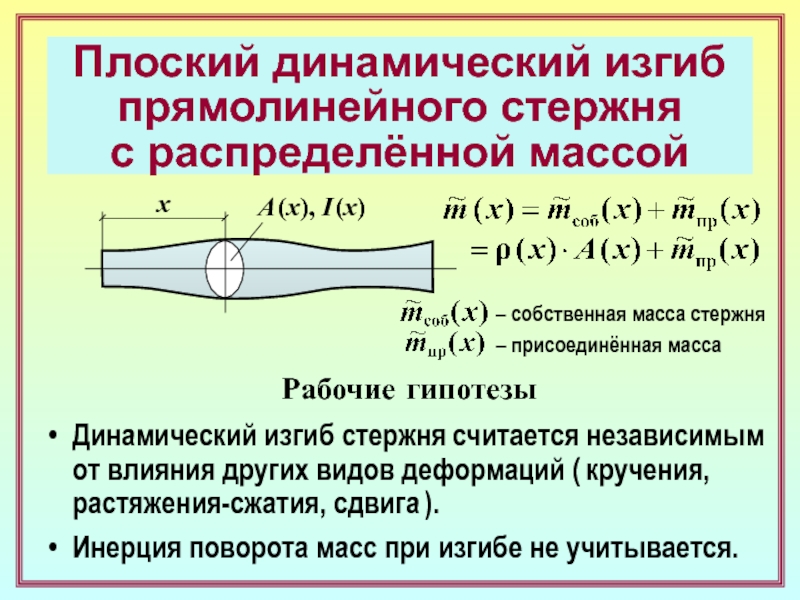
2. Какие рабочие гипотезы дополнительно вводятся в теории динамического изгиба
прямолинейных стержней с распределённой массой ( РМ )? ( 3 )
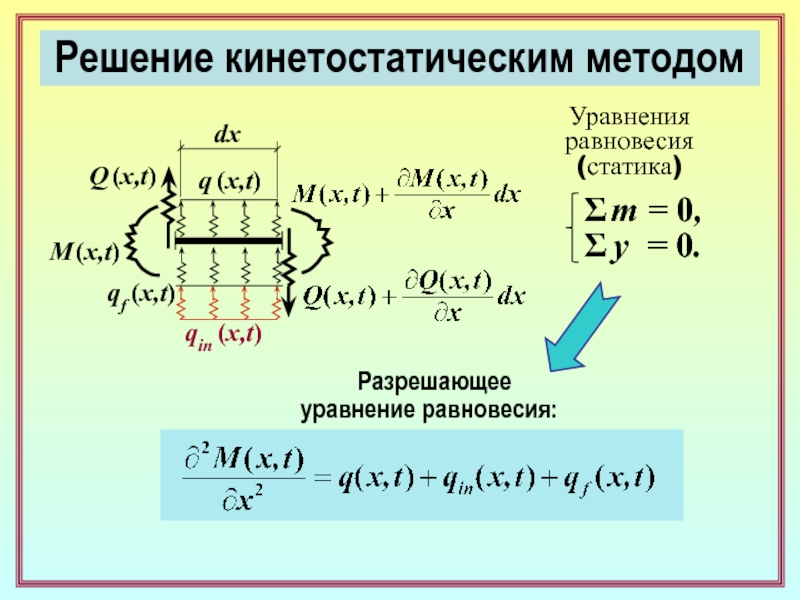
3. Расчётная схема в случае решения кинетостатическим методом задачи о свободных
изгибных колебаниях прямолинейного стержня с РМ. ( 5 )
4. Какие силовые факторы учитываются в статических уравнениях? ( 6 )
5. Как записываются геометрические соотношения? ( 7 )
6. Какие физические зависимости используются в решении задачи? ( 7 )
7. Вывод разрешающего дифференциального уравнения прогибов прямолинейного
стержня с РМ в общем случае свободного изгибного движения. ( 6 – 8 )
Частные случаи. ( 9 )
8. Как получается дифференциальное уравнение амплитуд прогибов стержня
постоянного сечения с равномерно распределённой массой в случае собственных
изгибных колебаний? ( 10 ) Какой вид имеет его решение? ( 11 )
9. Представление решения в балочных функциях Крылова. ( 11 )
Каковы свойства функций Крылова? ( 12 )
10. Выражения амплитуд динамических прогибов, углов поворота сечений, изгибающих
моментов и поперечных сил при собственных колебаниях в форме метода начальных
параметров ( МНП ). ( 15 ) , ( 19 )
11. Как учитывается в выражениях амплитуд характеристик напряжённо-деформирован-
ного состояния ( НДС ) стержня влияние сосредоточенных сил и моментов в произволь-
ных точках стержня? ( 19 ) Какими могут быть по физическому смыслу эти сосредото-
ченные воздействия при собственных колебаниях? ( 17 )
*) Только в режиме «Показ слайдов»



















![Динамика стержневых систем с распределенными массами Основные уравнения и уравнение частот собственных колебаний по МНП f * Основные уравнения и уравнение частот собственных колебаний по МНП f * W = 0v0θ0M0Q0[ R ]W =](/img/thumbs/9206a2268cc9537f2c08a19eee75a381-800x.jpg)