Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная алгебра и аналитическая геометрия
Содержание
- 1. Линейная алгебра и аналитическая геометрия
- 2. § 13. Прямая в пространстве1. Уравнения прямой
- 3. Другие формы записи уравнений прямой в пространстве
- 4. Уравнение (2*) и систему уравнений (2) называют параметрическими уравнениями
- 5. Частным случаем канонических уравнений являются УРАВНЕНИЯ ПРЯМОЙ,
- 6. 2. Переход от общих уравнений прямой к
- 7. 3. Взаимное расположение прямых в пространстве В
- 8. 2) Пусть прямые ℓ1 и ℓ2 пересекаются:Получили:
- 9. 4. Задачи, связанные с возможным взаимным расположением
- 10. ЗАДАЧА 2. Найти угол между пересекающимися (скрещива-
- 11. Пусть дана прямая
- 12. Пусть даны две скрещивающиеся прямые:
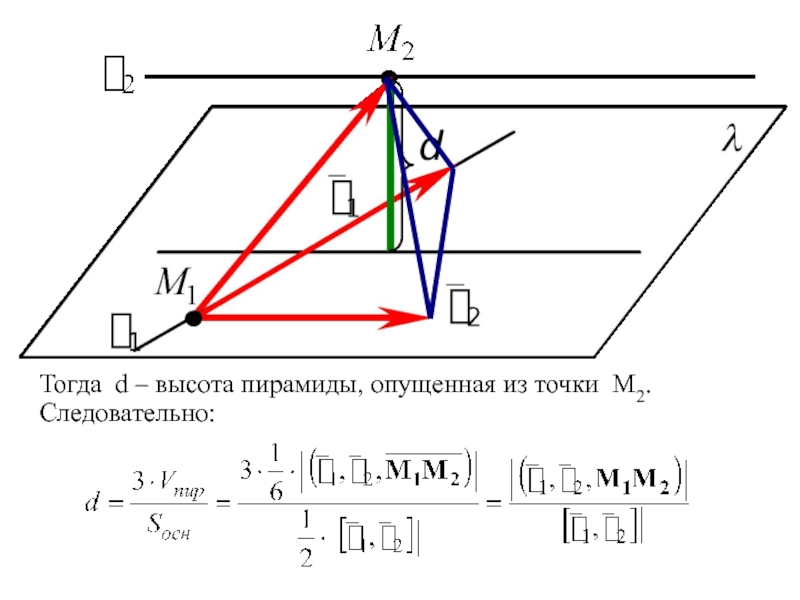
- 13. Тогда d – высота пирамиды, опущенная из точки M2. Следовательно:
- 14. ЗАДАЧА 5. Найти точку пересечения прямых. Пусть
- 15. 5. Взаимное расположение прямой и плоскости в
- 16. а) Если прямая параллельна плоскости или прямая принадлежит
- 17. Частным случаем пересечения прямой и плоскости в одной точке является перпендикулярность прямой и плоскости
- 18. ОПРЕДЕЛЕНИЕ. Углом между прямой ℓ и плоскостью
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Линейная алгебра и аналитическая геометрия
Лектор Белов В.М.
2010 г.
Тема:
Прямая в пространстве
Слайд 2§ 13. Прямая в пространстве
1. Уравнения прямой в пространстве
Пусть
A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 – уравнения любых двух
различных плоскостей, содержащих прямую ℓ .Тогда координаты любой точки прямой ℓ удовлетворяют одновременно обоим уравнениям, т.е. являются решениями системы
Систему (1) называют общими уравнениями прямой в пространстве.
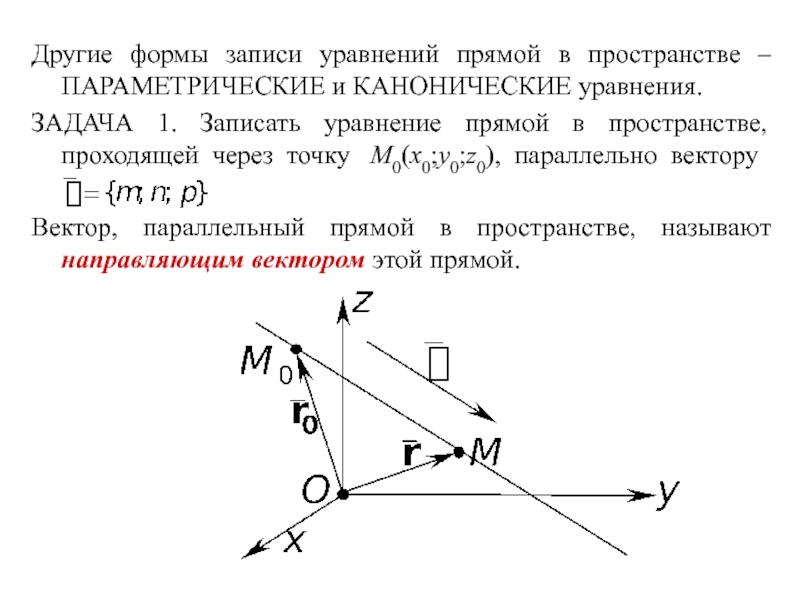
Слайд 3Другие формы записи уравнений прямой в пространстве – ПАРАМЕТРИЧЕСКИЕ и
КАНОНИЧЕСКИЕ уравнения.
ЗАДАЧА 1. Записать уравнение прямой в пространстве, проходящей через
точку M0(x0;y0;z0), параллельно вектору Вектор, параллельный прямой в пространстве, называют направляющим вектором этой прямой.
Слайд 4Уравнение (2*)
и систему уравнений (2)
называют параметрическими уравнениями прямой в про-
странстве
(в векторной и координатной форме соответ-
ственно).
Пусть в задаче 1 вектор
не параллелен ни одной из координатных осей (т.е. m 0, n 0 и p 0). Уравнения (3)
называют каноническими уравнениями прямой в пространстве.
Слайд 5Частным случаем канонических уравнений являются УРАВНЕНИЯ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ
ЗАДАННЫЕ ТОЧКИ.
Пусть прямая проходит через точки M1(x1,y1,z1) и M2(x2,y2
,z2) .Уравнения (4)
называют уравнениями прямой, проходящей через две точки M1(x1,y1,z1) и M2(x2,y2 ,z2) .
Слайд 62. Переход от общих уравнений прямой к каноническим
Пусть прямая
ℓ задана общими уравнениями:
Чтобы записать канонические (параметрические) уравнения этой
прямой, необходимо найти ее направляющий вектор и координаты какой-нибудь точки M0(x0;y0;z0) на прямой. а) Координаты точки M0 – это одно из решений системы (1).
б) Направляющий вектор
где N̄1 = {A1; B1; C1} и N̄2 = {A2; B2; C2} – нормальные векторы к плоскостям 1 и 2 , уравнения которых входят в общие уравнения прямой.
Слайд 73. Взаимное расположение прямых в пространстве
В пространстве две прямые
могут:
а) быть параллельны, б) пересекаться,
в) скрещиваться.Пусть прямые ℓ1 и ℓ2 заданы каноническими уравнениями:
1) Пусть прямые ℓ1 и ℓ2 параллельны:
Получаем: прямые параллельны их направляющие векто-
ры и коллинеарные, т.е. выполняется условие:
Слайд 82) Пусть прямые ℓ1 и ℓ2 пересекаются:
Получили: прямые ℓ1 и
ℓ2 пересекаются они не параллельны и для них выполняется
условиеили, в координатной форме,
3) Если для прямых ℓ1 и ℓ2 не выполняется условие (6) и (7) ((7*)), то прямые скрещиваются.
Слайд 94. Задачи, связанные с возможным взаимным расположением прямых
Возможное расположение прямых
в пространстве приводит к следующим задачам:
1) параллельные прямые расстояние между
прямыми(т.е. расстояние от точки до прямой)?
2) пересекающиеся прямые а) угол между прямыми?
б) точка пересечения прямых?
3) скрещивающиеся прямые а) угол между прямыми?
б) расстояние между прямыми?
Пусть даны 2 прямые:
и
– направляющий вектор прямой ℓi ,
Mi(xi;yi;zi) ℓi (i = 1,2)
Слайд 10ЗАДАЧА 2. Найти угол между пересекающимися (скрещива-
ющимися) прямыми в пространстве.
ОПРЕДЕЛЕНИЕ.
Углом между двумя скрещивающимися прямыми ℓ1 и ℓ2 называется угол
между прямой ℓ1 и проекцией прямой ℓ2 на любую плоскость, проходящую через прямую ℓ1 .Т.е., угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, параллельными данным.
Получаем:
где знак плюс берется для острого угла, а знак минус – для тупого.
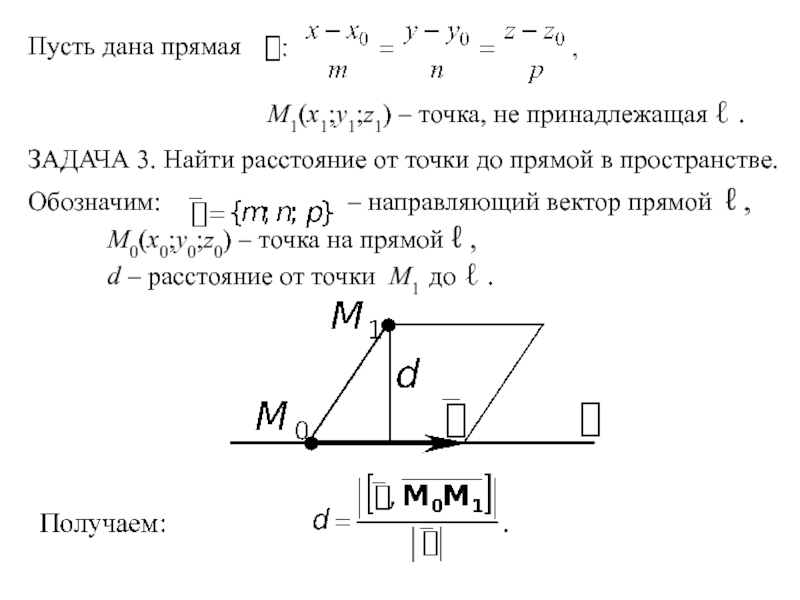
Слайд 11Пусть дана прямая
M1(x1;y1;z1) – точка, не принадлежащая ℓ .
ЗАДАЧА 3. Найти расстояние от точки до прямой в пространстве.
Обозначим: – направляющий вектор прямой ℓ ,
M0(x0;y0;z0) – точка на прямой ℓ ,
d – расстояние от точки M1 до ℓ .
Слайд 12Пусть даны две скрещивающиеся прямые:
и
– направляющий вектор прямой ℓi ,
Mi(xi;yi;zi) ℓi (i = 1,2) .
ЗАДАЧА 4. Найти расстояние между ℓ1 и ℓ2 .
ОПРЕДЕЛЕНИЕ. Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра.
где Ax + By + Cz + D = 0 – общее уравнение плоскости λ ,
M2(x2; y2; z2) – любая точка на прямой ℓ2 .
Слайд 14ЗАДАЧА 5. Найти точку пересечения прямых.
Пусть M0(x0;y0;z0) –
точка пересечения прямых.
Тогда (x0;y0;z0) – решение системы уравнений
Слайд 155. Взаимное расположение прямой и плоскости в пространстве
Пусть в
пространстве заданы плоскость λ и прямая ℓ . Они могут
1) быть параллельны;2) прямая может лежать в плоскости;
3) прямая и плоскость могут пересекаться в одной точке.
Пусть λ: Ax + By + Cz + D = 0 и
Тогда N̄ = {A; B; C} – нормальный вектор плоскости λ,
– направляющий вектор прямой ℓ .
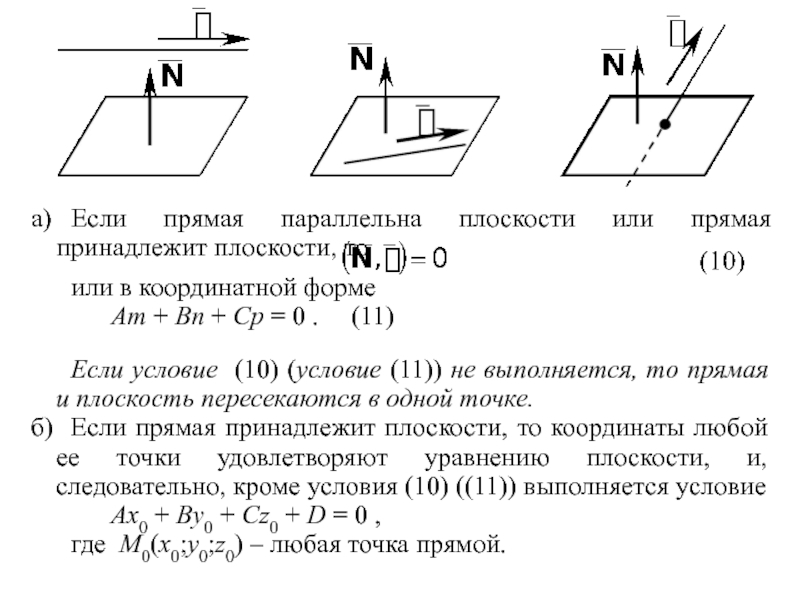
Слайд 16а) Если прямая параллельна плоскости или прямая принадлежит плоскости, то
или в
координатной форме
Am + Bn + Cp = 0
. (11) Если условие (10) (условие (11)) не выполняется, то прямая и плоскость пересекаются в одной точке.
б) Если прямая принадлежит плоскости, то координаты любой ее точки удовлетворяют уравнению плоскости, и, следовательно, кроме условия (10) ((11)) выполняется условие
Ax0 + By0 + Cz0 + D = 0 ,
где M0(x0;y0;z0) – любая точка прямой.
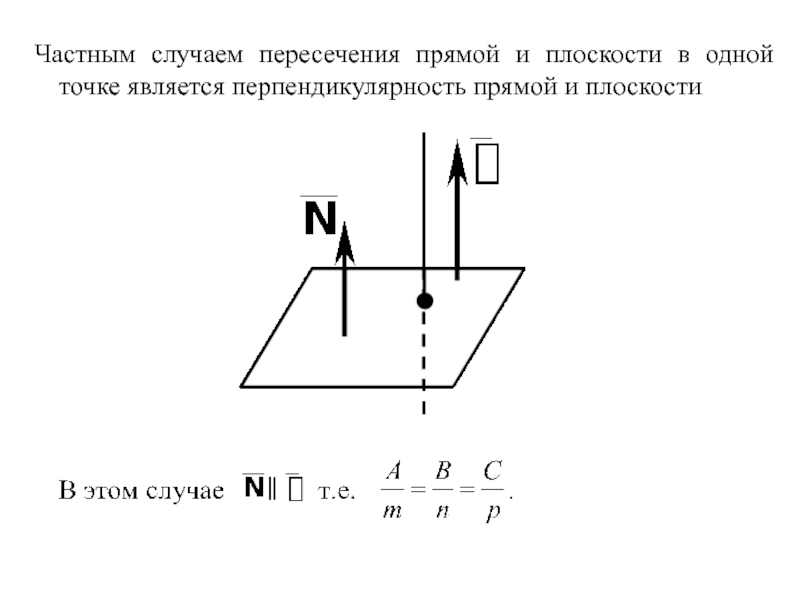
Слайд 17Частным случаем пересечения прямой и плоскости в одной точке является
перпендикулярность прямой и плоскости
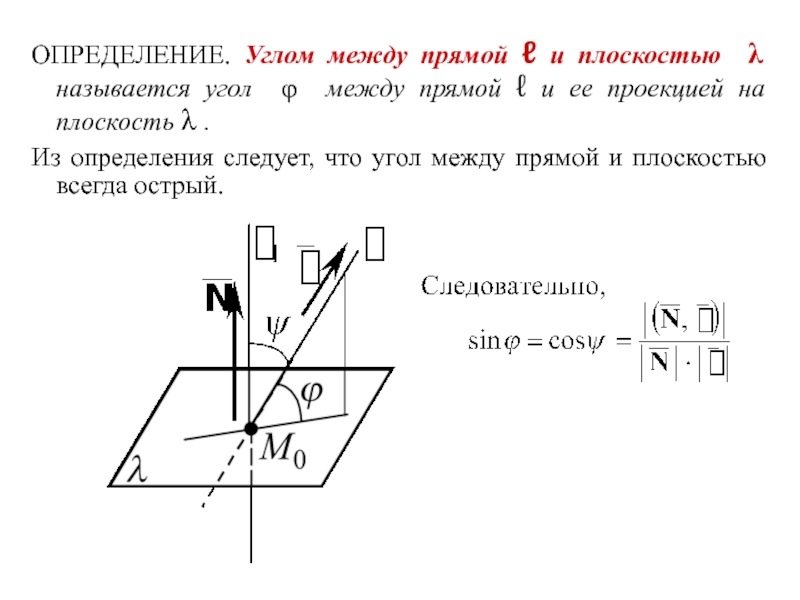
Слайд 18ОПРЕДЕЛЕНИЕ. Углом между прямой ℓ и плоскостью λ называется угол
φ между прямой ℓ и ее проекцией на плоскость λ
.Из определения следует, что угол между прямой и плоскостью всегда острый.