Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 2
Содержание
- 1. Лекция 2
- 2. Ортогональная проекция плоскостиПлоскость является простейшей поверхностью. Положение
- 3. Задание плоскости на комплексном чертеже Для
- 4. Задание плоскости на комплексном чертеже Для
- 5. Задание плоскостив) с помощью задания проекций двух прямых, пересекающихся в собственной или несобственной точке
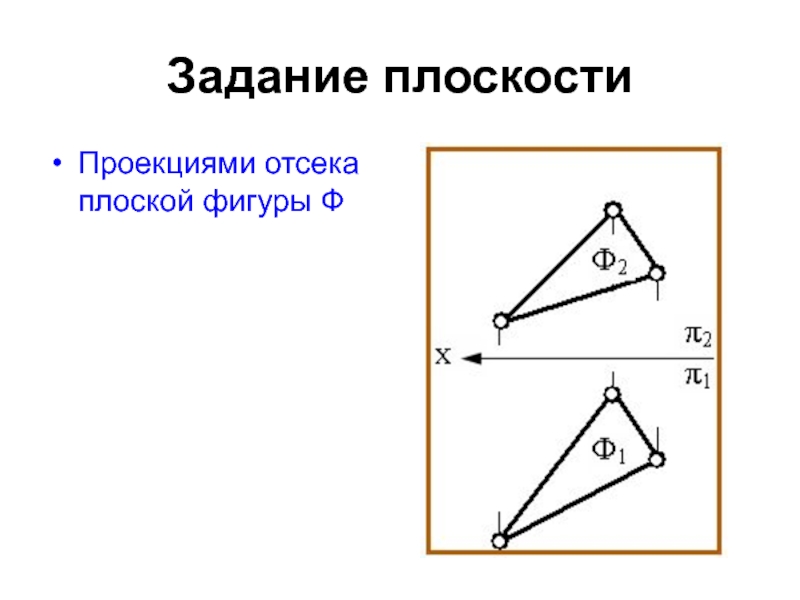
- 6. Задание плоскостиПроекциями отсека плоской фигуры Ф
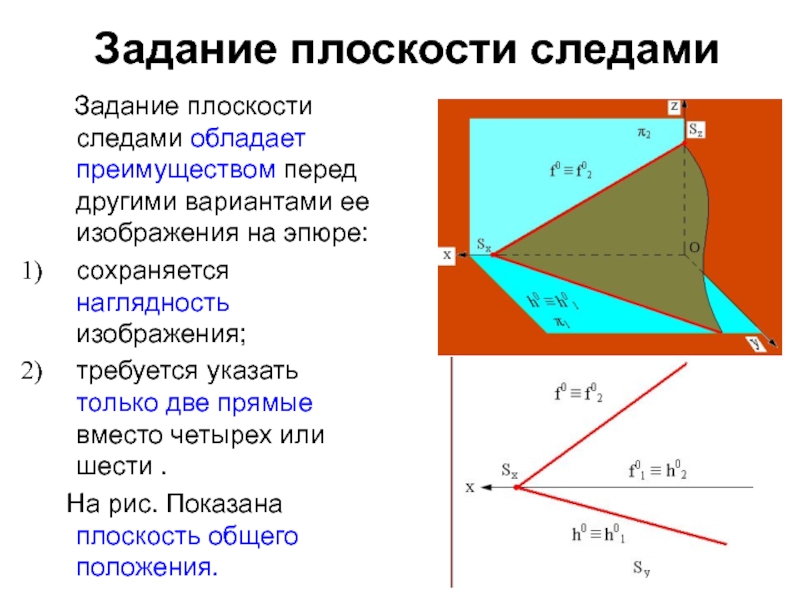
- 7. Задание плоскости следами Задание плоскости
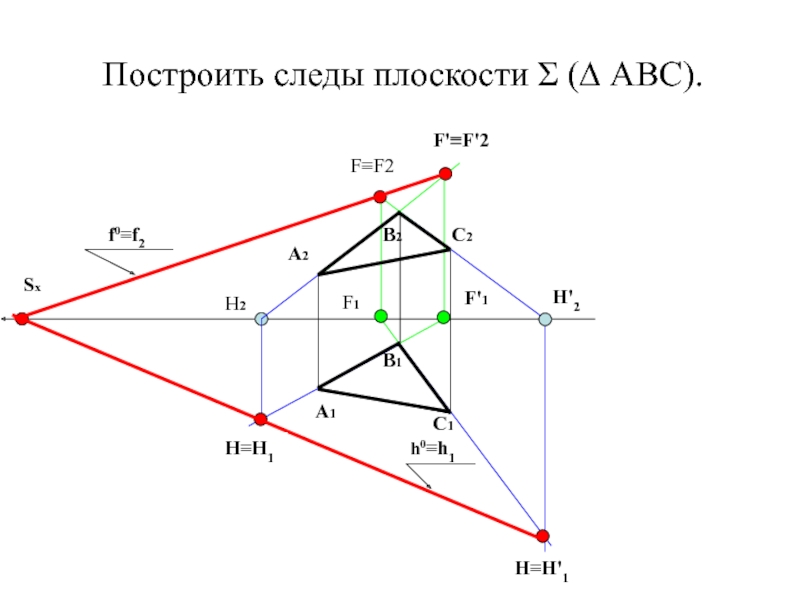
- 8. Построить следы плоскости Σ (∆ АВС).А1А2В2В1С2С1SxF1H2F≡F2F'≡F'2F'1 Н≡Н1Н≡Н'1Н'2 h0≡h1 f0≡f2
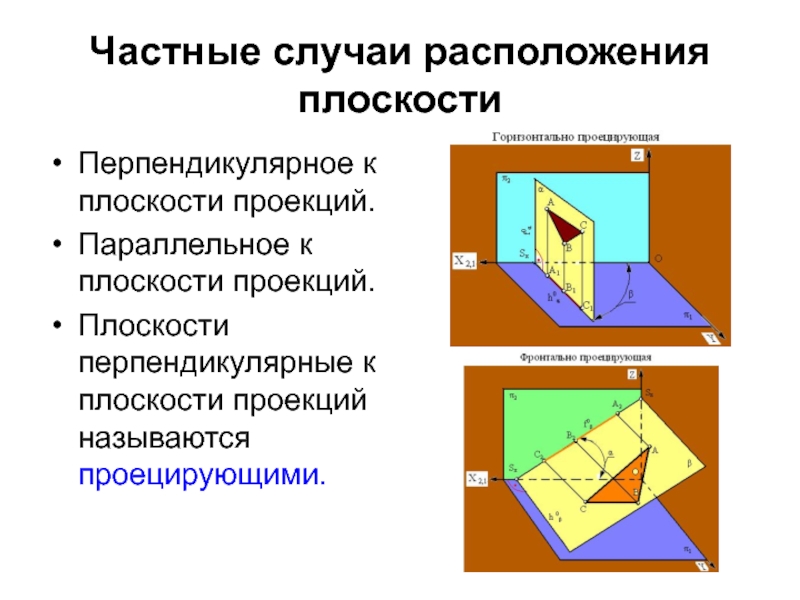
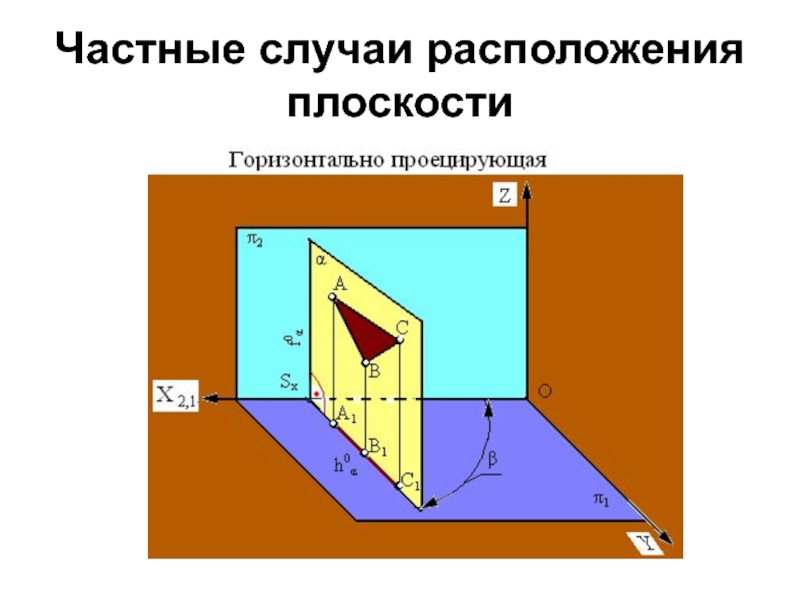
- 9. Частные случаи расположения плоскостиПерпендикулярное к плоскости проекций.Параллельное к плоскости проекций.Плоскости перпендикулярные к плоскости проекций называются проецирующими.
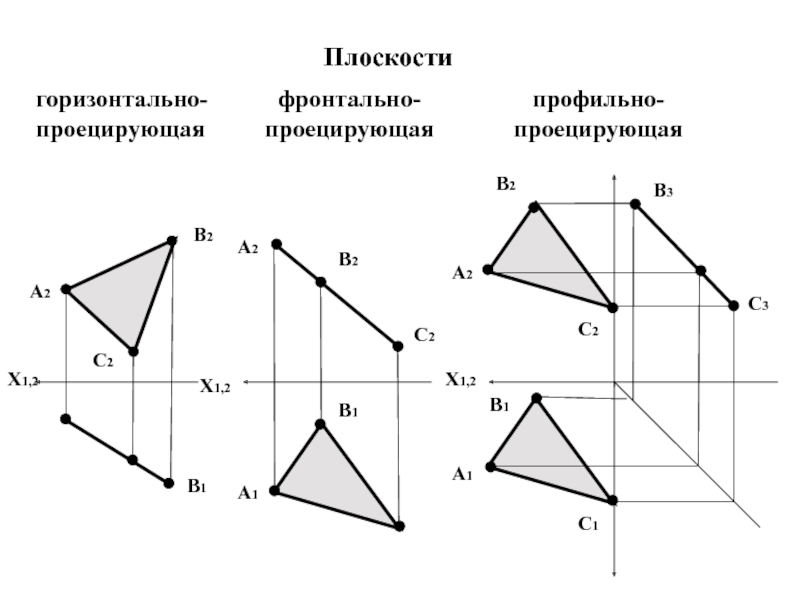
- 10. горизонтально-проецирующая фронтально-проецирующая профильно-проецирующая Плоскости Х1,2А1А2А1А2А2В3В2В2В2С2С3С2С2В1В1В1С1Х1,2Х1,2
- 11. Частные случаи расположения плоскости
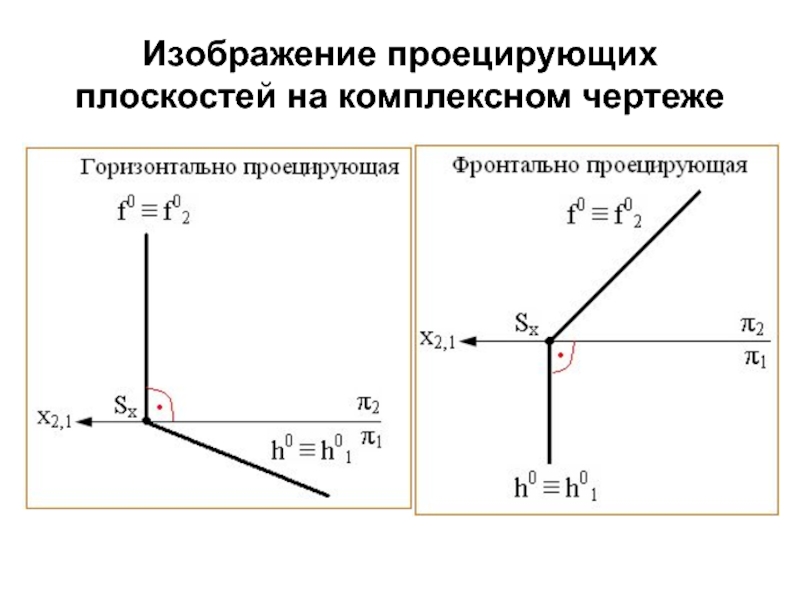
- 12. Изображение проецирующих плоскостей на комплексном чертеже
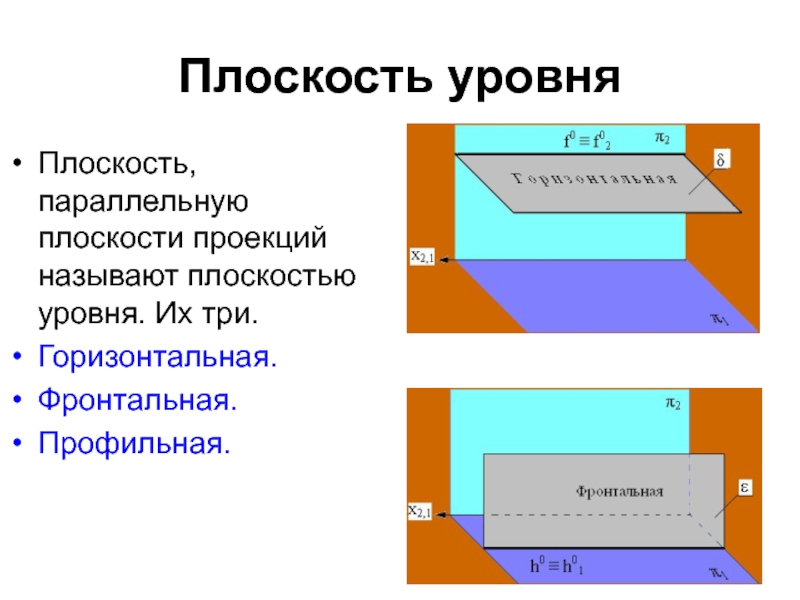
- 13. Плоскость уровня Плоскость, параллельную плоскости проекций называют плоскостью уровня. Их три.Горизонтальная.Фронтальная.Профильная.
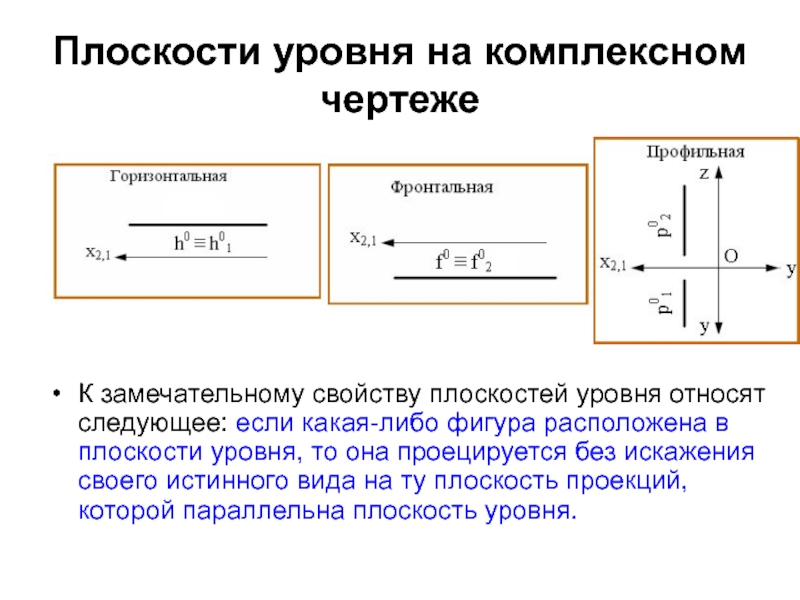
- 14. Плоскости уровня на комплексном чертежеК замечательному свойству
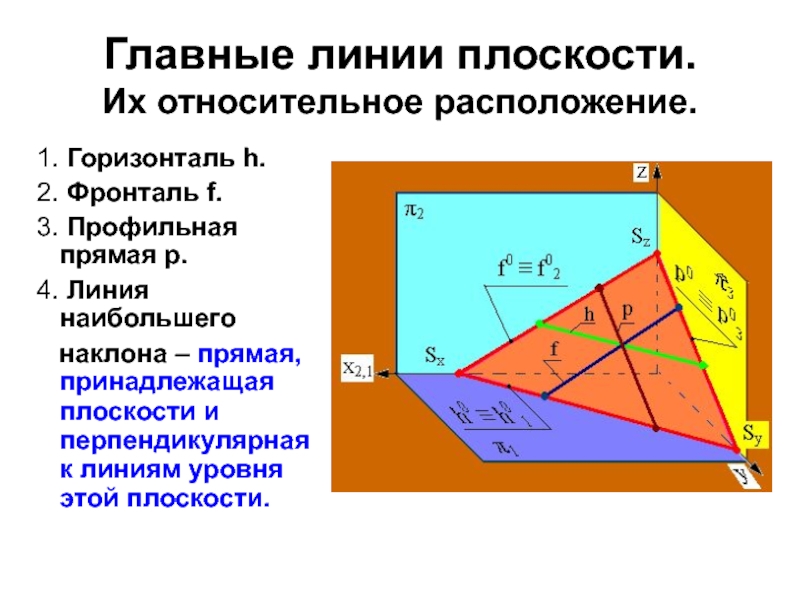
- 15. Главные линии плоскости. Их относительное расположение.
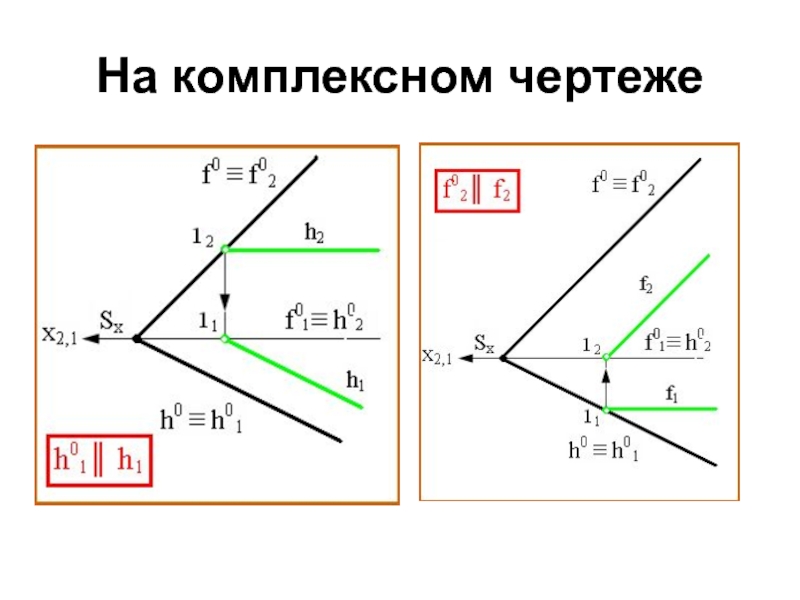
- 16. На комплексном чертеже
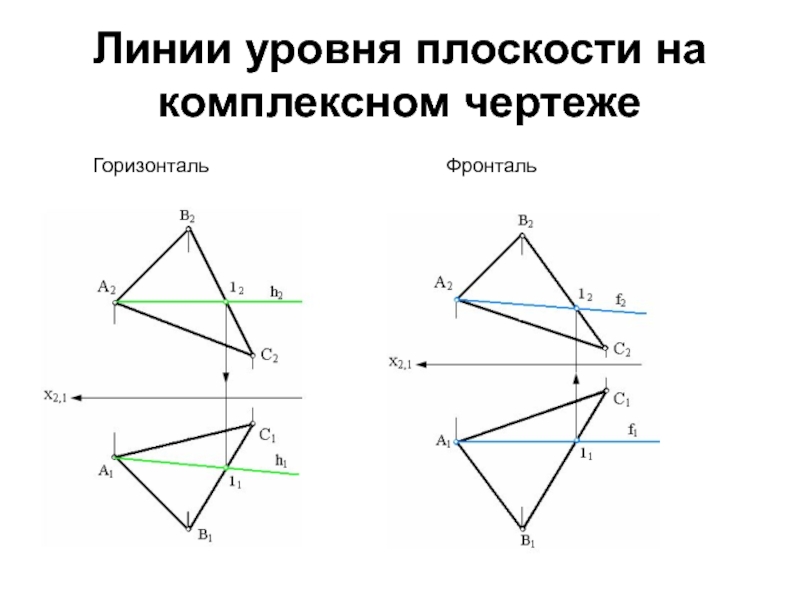
- 17. Линии уровня плоскости на комплексном чертежеГоризонтальФронталь
- 18. Линия наибольшего наклона плоскостис – линия наибольшего наклона плоскости к горизонтальной плоскости проекций (линия ската).С
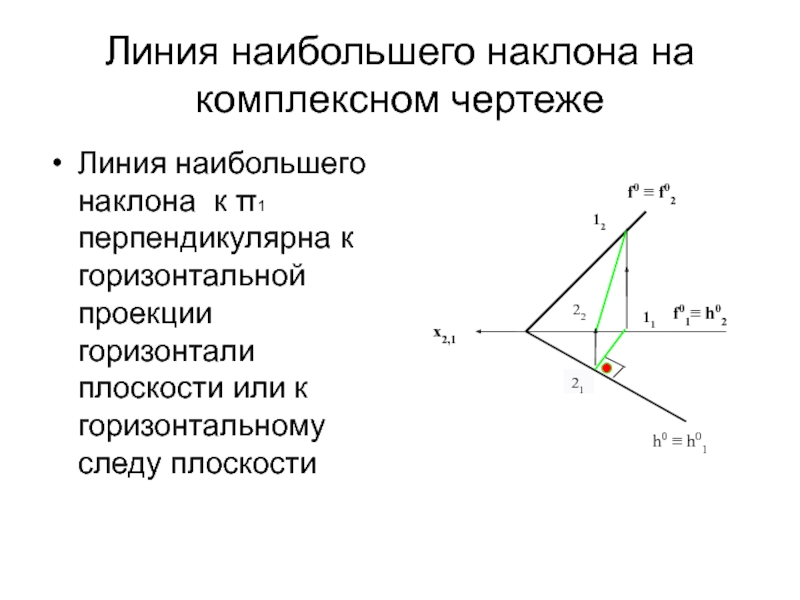
- 19. Линия наибольшего наклона на комплексном чертежеЛиния наибольшего
- 20. Определение расстояния между двумя точками способом прямоугольного
- 21. Пример определения расстояния способом прямоугольного треугольникаX2,1A2B2B1A1A0A0αºβºНатуральная величинаyAyB∆y
- 22. Параллельность плоскостей. Из элементарной геометрии известна
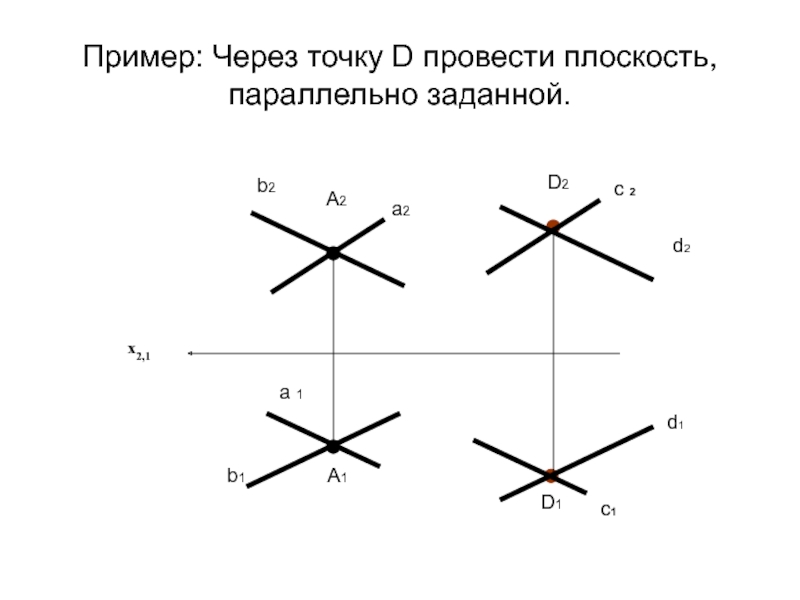
- 23. Пример: Через точку D провести плоскость, параллельно заданной.x2,1b2b1a 1a2A2A1D2D1c 2c1d2d1
- 24. Скачать презентанцию
Ортогональная проекция плоскостиПлоскость является простейшей поверхностью. Положение плоскости в пространстве однозначно определяется тремя различными точками, не принадлежащими одной прямой.
Слайды и текст этой презентации
Слайд 2Ортогональная проекция плоскости
Плоскость является простейшей поверхностью.
Положение плоскости в пространстве
однозначно определяется тремя различными точками, не принадлежащими одной прямой.
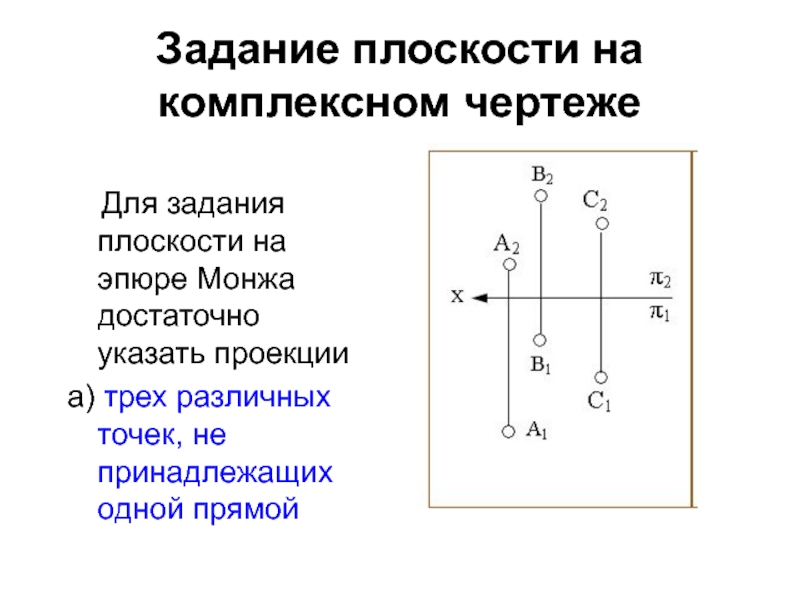
Слайд 3Задание плоскости на комплексном чертеже
Для задания плоскости на
эпюре Монжа достаточно указать проекции
а) трех различных точек, не принадлежащих
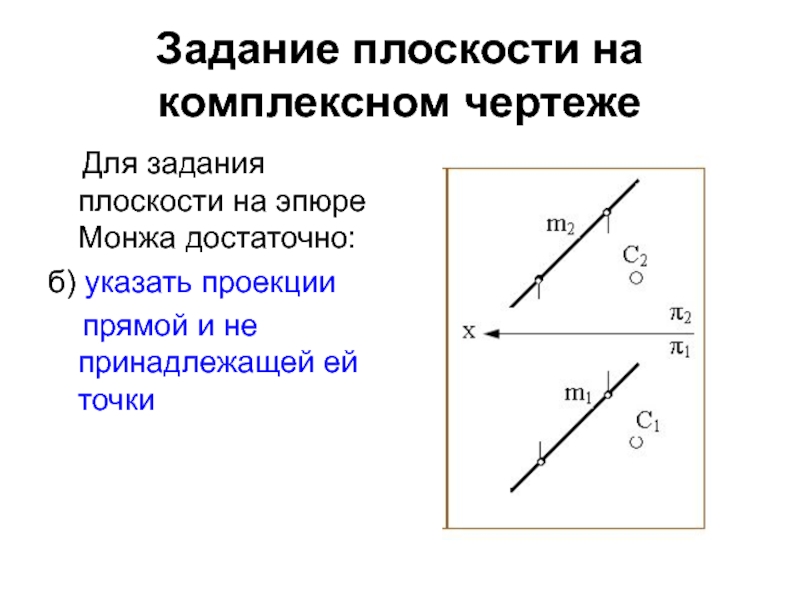
одной прямойСлайд 4Задание плоскости на комплексном чертеже
Для задания плоскости на
эпюре Монжа достаточно:
б) указать проекции
прямой и
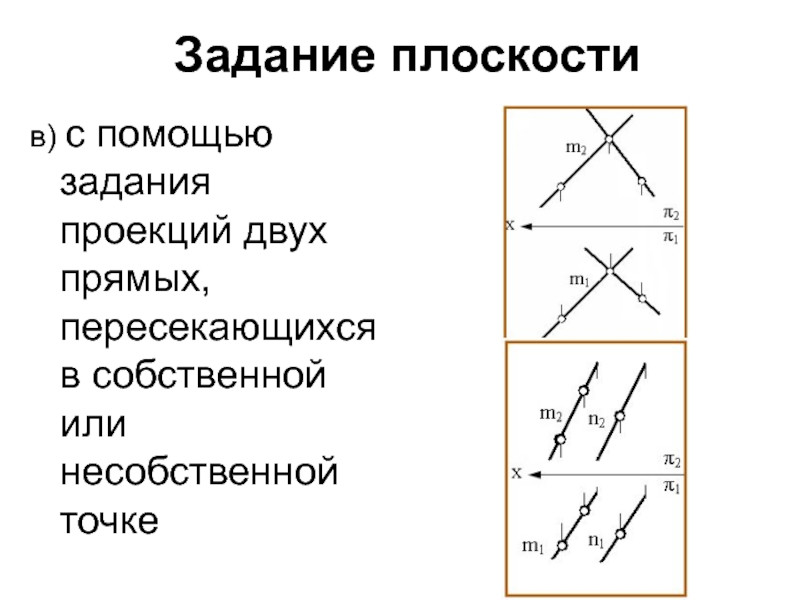
не принадлежащей ей точкиСлайд 5Задание плоскости
в) с помощью задания проекций двух прямых, пересекающихся в
собственной или несобственной точке
Слайд 7Задание плоскости следами
Задание плоскости следами обладает преимуществом
перед другими вариантами ее изображения на эпюре:
сохраняется наглядность изображения;
требуется
указать только две прямые вместо четырех или шести . На рис. Показана плоскость общего положения.
Слайд 9Частные случаи расположения плоскости
Перпендикулярное к плоскости проекций.
Параллельное к плоскости проекций.
Плоскости
перпендикулярные к плоскости проекций называются проецирующими.
Слайд 10горизонтально-проецирующая
фронтально-проецирующая
профильно-проецирующая
Плоскости
Х1,2
А1
А2
А1
А2
А2
В3
В2
В2
В2
С2
С3
С2
С2
В1
В1
В1
С1
Х1,2
Х1,2
Слайд 13Плоскость уровня
Плоскость, параллельную плоскости проекций называют плоскостью уровня. Их
три.
Горизонтальная.
Фронтальная.
Профильная.
Слайд 14Плоскости уровня на комплексном чертеже
К замечательному свойству плоскостей уровня относят
следующее: если какая-либо фигура расположена в плоскости уровня, то она
проецируется без искажения своего истинного вида на ту плоскость проекций, которой параллельна плоскость уровня.Слайд 15Главные линии плоскости.
Их относительное расположение.
1. Горизонталь h.
2.
Фронталь f.
3. Профильная прямая p.
4. Линия наибольшего
наклона – прямая, принадлежащая плоскости и перпендикулярная к линиям уровня этой плоскости.Слайд 18Линия наибольшего наклона плоскости
с – линия наибольшего наклона плоскости к
горизонтальной плоскости проекций (линия ската).
С
Слайд 19Линия наибольшего наклона на комплексном чертеже
Линия наибольшего наклона к π1
перпендикулярна
к горизонтальной проекции горизонтали плоскости или к горизонтальному следу плоскости11
12
21
22
x2,1
f0 ≡ f02
h0 ≡ h01
f01≡ h02
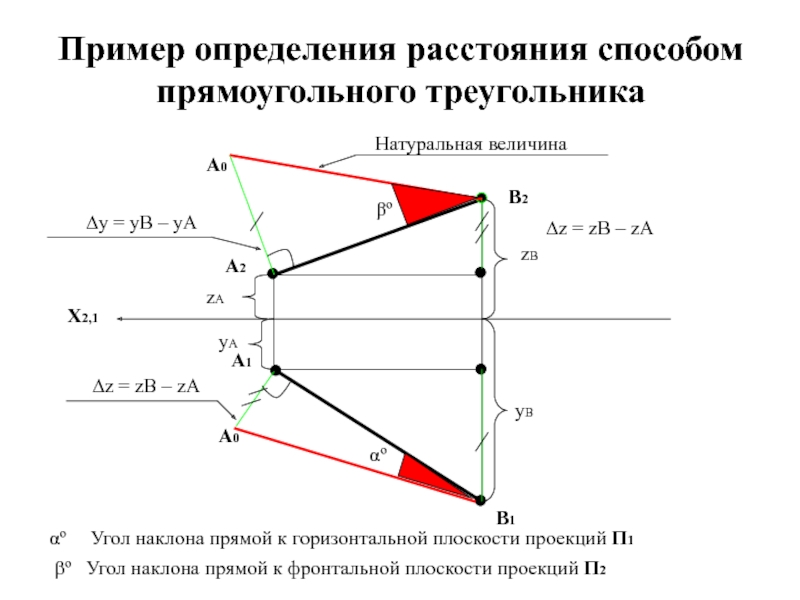
Слайд 20Определение расстояния между двумя точками способом прямоугольного треугольника
Натуральная величина отрезка
равна гипотенузе прямоугольного треугольника, построенного на двух катетах один из
которых проекция отрезка, а второй – разница координат начала и конца отрезка в другой плоскости проекций.Слайд 21Пример определения расстояния способом прямоугольного треугольника
X2,1
A2
B2
B1
A1
A0
A0
αº
βº
Натуральная величина
yA
yB
∆y = yB –
yA
zB
zA
∆z = zB – zA
αº
Угол наклона прямой к
горизонтальной плоскости проекций П1βº Угол наклона прямой к фронтальной плоскости проекций П2
∆z = zB – zA
Слайд 22
Параллельность плоскостей.
Из элементарной геометрии известна теорема (признак параллельности плоскостей):
Если две
пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны.Следствие: если плоскости заданы следами и одноименные следы плоскостей параллельны, то и плоскости параллельны.
Из этого соотношения следует, что если хотя бы одна пара одноименных следов пересекается, то и плоскости пересекаются.
Из этих определений легко вывести способ построения параллельных плоскостей на чертеже