Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика твердого тела. Момент инерции
Содержание
- 1. Динамика твердого тела. Момент инерции
- 2. Момент инерции твердого телаМоментом инерции твердого тела
- 3. Физический смысл и свойства момента инерцииМомент инерции
- 4. Моменты инерции некоторых симметричных твердых тел
- 5. Момент импульса частицы относительно неподвижной точкиПусть частица
- 6. Момент импульса частицы относительно неподвижной осиМоментом импульса
- 7. Связь между угловой скоростью вращения твердого тела
- 8. Момент силыПусть к частице A приложена сила
- 9. Момент силы относительно неподвижной осиМоментом силы Mz
- 10. Уравнение моментовНайдем производную по времени момента импульса L:Производная:Тогда
- 11. Уравнение вращения твердого тела вокруг неподвижной осиПусть
- 12. Уравнение вращения твердого тела вокруг неподвижной осиПоскольку,
- 13. Пример использования уравнения вращения твердого тела вокруг
- 14. Пример использования уравнения вращения твердого тела вокруг
- 15. ГЛАВА 5 ДИНАМИКА ТВЕРДОГО ТЕЛА5.2 Теорема Гюйгенса – Штейнера
- 16. Связь между моментами инерции твердого тела относительно
- 17. Связь между моментами инерции твердого тела относительно
- 18. Связь между моментами инерции твердого тела относительно
- 19. Примеры использования теоремы Гюйгенса - ШтейнераПример 1.
- 20. Примеры использования теоремы Гюйгенса - ШтейнераПример 2.
- 21. ГЛАВА 5 ДИНАМИКА ТВЕРДОГО ТЕЛА5.3
- 22. Кинетическая энергия твердого телаПусть твердое тело вращается
- 23. Кинетическая энергия твердого телаТаким образом, кинетическая энергия
- 24. Работа внешней силы при вращении твердого тела
- 25. Работа внешней силы при вращении твердого тела
- 26. Работа внешней силы при вращении твердого тела
- 27. ГЛАВА 5 ДИНАМИКА ТВЕРДОГО ТЕЛА5.4 Закон сохранения момента импульса системы частиц
- 28. Закон сохранения момента импульса системы частицИз уравнения
- 29. Частные случаи закона сохранения момента импульса незамкнутой
- 30. Частные случаи закона сохранения момента импульса незамкнутой
- 31. Частные случаи закона сохранения момента импульса незамкнутой
- 32. Частные случаи закона сохранения момента импульса незамкнутой
- 33. Частные случаи закона сохранения момента импульса незамкнутой
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ГЛАВА 5
ДИНАМИКА
ТВЕРДОГО ТЕЛА
5.1 Момент инерции. Момент импульса частицы.
Момент силы. Уравнение моментов.
Слайд 2Момент инерции твердого тела
Моментом инерции твердого тела относительно оси Z
называется величина:
Здесь mi – масса i-й частицы тела; Ri –
расстояние от этой частицы до оси Z.Поскольку любое реальное твердое тело плотности ρ и объемом V есть совокупность бесконечно большого числа частиц, то
Слайд 3Физический смысл и свойства момента инерции
Момент инерции I характеризует распределение
массы тела по его объему.
Эта величина представляет собой количественную
меру инертности твердого тела по отношению к любым попыткам изменить угловую скорость твердого тела.Момент инерции – величина аддитивная: момент инерции тела относительно некоторой оси равен сумме моментов инерции его частей, рассчитанных относительно той же оси.
Слайд 5Момент импульса частицы относительно неподвижной точки
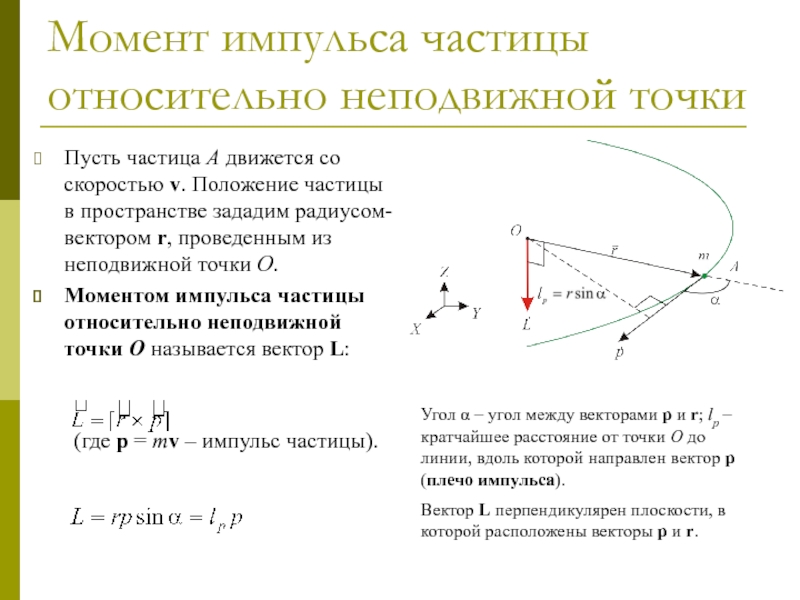
Пусть частица A движется со
скоростью v. Положение частицы в пространстве зададим радиусом-вектором r, проведенным
из неподвижной точки O.Моментом импульса частицы относительно неподвижной точки O называется вектор L:
(где p = mv – импульс частицы).
Угол α – угол между векторами p и r; lp – кратчайшее расстояние от точки O до линии, вдоль которой направлен вектор p (плечо импульса).
Вектор L перпендикулярен плоскости, в которой расположены векторы p и r.
Слайд 6Момент импульса частицы относительно неподвижной оси
Моментом импульса Lz частицы относительно
неподвижной оси Z называется проекция на эту ось момента импульса
L частицы, вычисленная относительно неподвижной точки оси Z.Момент импульса Lz относительно неподвижной оси является скалярной величиной
Значение Lz не зависит от выбора точки O на оси Z.
Слайд 7Связь между угловой скоростью вращения твердого тела и моментом импульса
Таким
образом, с учетом определения момента инерции, проекция на ось Z
момента импульса тела равна:Проекция момента импульса тела Lz на ось Z не зависит от положения точки O на этой оси (поскольку I и ωz также не зависят от положения точки O).
Слайд 8Момент силы
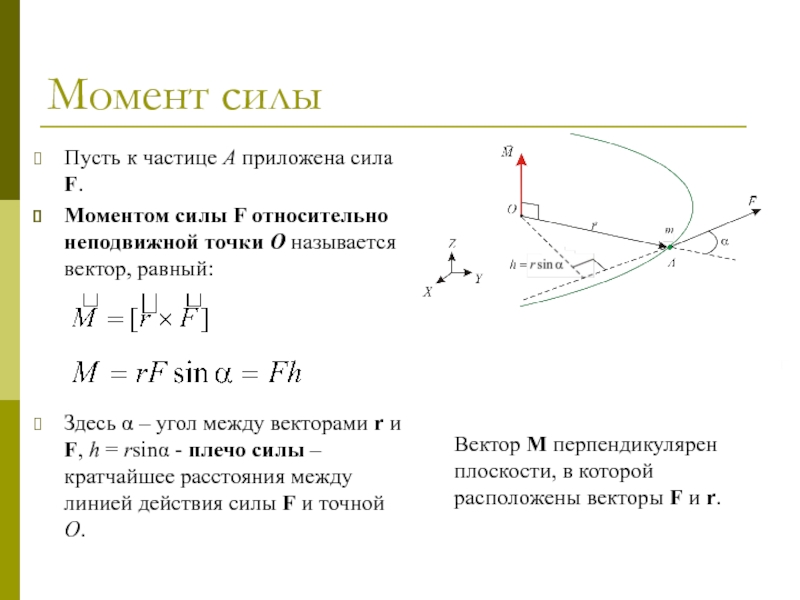
Пусть к частице A приложена сила F.
Моментом силы F
относительно неподвижной точки O называется вектор, равный:
Здесь α – угол
между векторами r и F, h = rsinα - плечо силы – кратчайшее расстояния между линией действия силы F и точной O.Вектор M перпендикулярен плоскости, в которой расположены векторы F и r.
Слайд 9Момент силы относительно неподвижной оси
Моментом силы Mz относительно неподвижной оси
Z называется проекция на эту ось вектора момента силы относительно
произвольной точки O на оси Z.Величина Mz является скалярной и не зависит от выбора точки O на оси Z.
Слайд 11Уравнение вращения твердого тела вокруг неподвижной оси
Пусть твердое тело вращается
с угловой скоростью ω вокруг неподвижной оси Z. Обозначим через
L момент импульса тела относительно произвольной точки O оси Z, а через M – сумму моментов всех приложенных к нему внешних сил.Для твердого тела как системы материальных точек справедливо уравнение моментов:
Перепишем его в проекции на ось Z:
Слайд 12Уравнение вращения твердого тела вокруг неподвижной оси
Поскольку, как было показано
выше, проекция на ось Z момента импульса тела равна Lz
= Iωz, то подставляя это выражение в уравнение моментов, получим уравнение вращения твердого тела вокруг неподвижной оси:Здесь I – момент инерции твердого тела относительно оси Z, εz = dωz/dt – проекция на ось Z вектора углового ускорения тела, Mz – проекция на ось Z момента всех внешних сил.
Слайд 13Пример использования уравнения вращения твердого тела вокруг неподвижной оси
Пример. Однородный
цилиндр массы m и радиуса R может вращаться с трением
вокруг неподвижной оси Z, совпадающей с его осью симметрии. На цилиндр намотана тонкая нерастяжимая невесомая нить, за которую начинают тянуть с постоянной силой F. Найти угловые скорость и ускорение цилиндра, если во время вращения на цилиндр действует постоянный момент силы трения Mтр.Слайд 14Пример использования уравнения вращения твердого тела вокруг неподвижной оси
Направим ось
Z от нас в плоскость чертежа и запишем уравнение динамики
вращения твердого тела:Тогда угловое ускорение цилиндра:
Угловая скорость цилиндра:
Слайд 16Связь между моментами инерции твердого тела относительно двух параллельных осей,
одна из которых проводит через центр масс
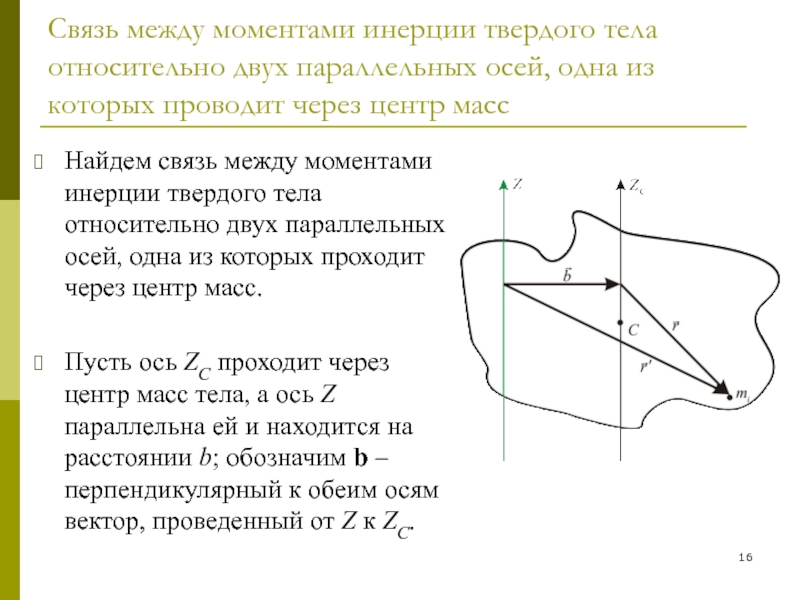
Найдем связь между моментами
инерции твердого тела относительно двух параллельных осей, одна из которых проходит через центр масс.Пусть ось ZC проходит через центр масс тела, а ось Z параллельна ей и находится на расстоянии b; обозначим b – перпендикулярный к обеим осям вектор, проведенный от Z к ZC.
Слайд 17Связь между моментами инерции твердого тела относительно двух параллельных осей,
одна из которых проводит через центр масс
Мысленно разделим тело на
частицы массами mi; к каждой частице проведем радиусы-векторы ri и ri′, перпендикулярные осям ZC и Z.Учтем в дальнейшем, что ri′ = ri + b.
Момент инерции относительно оси Z:
Слайд 18Связь между моментами инерции твердого тела относительно двух параллельных осей,
одна из которых проводит через центр масс
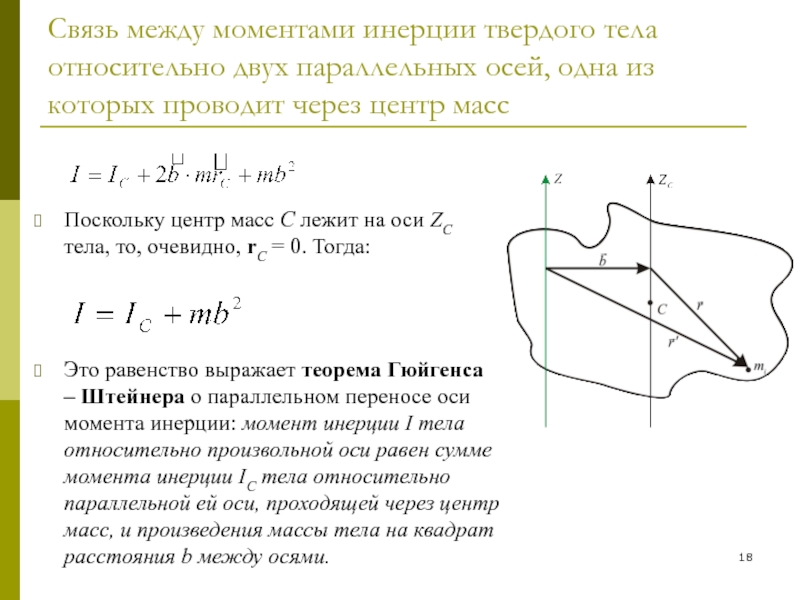
Поскольку центр масс C
лежит на оси ZC тела, то, очевидно, rС = 0. Тогда:Это равенство выражает теорема Гюйгенса – Штейнера о параллельном переносе оси момента инерции: момент инерции I тела относительно произвольной оси равен сумме момента инерции IC тела относительно параллельной ей оси, проходящей через центр масс, и произведения массы тела на квадрат расстояния b между осями.
Слайд 19Примеры использования теоремы Гюйгенса - Штейнера
Пример 1. Зная момент инерции
тонкого стержня массы m и длины l относительно оси, перпендикулярной
к стержню и проходящей через его середину (центр масс) I = (1/12)ml2, найдем момент инерции стержня относительно параллельной оси, проходящей через один из концов стержня:
Слайд 20Примеры использования теоремы Гюйгенса - Штейнера
Пример 2. Зная момент инерции
однородного шара массы m и радиуса R относительно оси, проходящей
через его центр (центр масс) I = (2/5)mR2, найдем момент инерции шара относительно оси, касательной к поверхности шара:
Слайд 21ГЛАВА 5
ДИНАМИКА
ТВЕРДОГО ТЕЛА
5.3 Кинетическая энергия и работа внешних
сил при вращении твердого тела вокруг неподвижной оси
Слайд 22Кинетическая энергия твердого тела
Пусть твердое тело вращается вокруг неподвижной оси
Z с угловой скоростью ω. Разделим мысленно тело на частицы
массами mi.Траекторией каждой из частиц является окружность с центром на оси вращения, лежащая в перпендикулярной к оси вращения плоскости. Обозначим скорость каждой из частиц vi = ωRi.
Кинетическая энергия Κ твердого тела равна сумме кинетических энергий составляющих его частиц:
Слайд 23Кинетическая энергия твердого тела
Таким образом, кинетическая энергия твердого тела, вращающегося
вокруг неподвижной оси, равна:
Здесь I – момент инерции тела относительно
оси вращения.
Слайд 24Работа внешней силы при вращении твердого тела вокруг неподвижной оси
Пусть
на вращающееся вокруг неподвижной оси Z твердое тело действует внешняя
сила F, проекция на ось Z момента M которой равна Mz. Найдем выражение для работы A силы, снова рассматривая твердое тело как систему частиц.По теореме о кинетической энергии элементарная работа δA всех сил, действующих на частицы, равна бесконечно малому приращению кинетической энергии dΚ системы:
Примем без доказательства, что элементарная работа всех внутренних сил равна нулю.
Слайд 25Работа внешней силы при вращении твердого тела вокруг неподвижной оси
Тогда
теорема о кинетической энергии применительно к твердому телу звучит так:
работа всех приложенных к твердому телу внешних сил равна приращению его кинетической энергии:Согласно уравнению вращения твердого тела вокруг неподвижной оси:
Слайд 26Работа внешней силы при вращении твердого тела вокруг неподвижной оси
Тогда
элементарное приращение кинетической энергии твердого тела:
Здесь ϕ – угловая координата,
dϕ – угол, на который поворачивается тело за бесконечно малый промежуток времени dt.Таким образом,
Слайд 28Закон сохранения момента импульса системы частиц
Из уравнения моментов вытекает закон
сохранения импульса системы частиц: момент импульса L замкнутой системы частиц
с течением времени не изменяется (т.е. сохраняется).Действительно, если система замкнута, т.е. внешние силы отсутствуют, то:
Однако, в некоторых случаях момент импульса незамкнутой системы частиц может сохраняться. Рассмотрим эти случаи.
Слайд 29Частные случаи закона сохранения момента импульса незамкнутой системы частиц
1. Если
система не замкнута, но моменты внешних сил, вообще говоря, отличны
от нуля, но при этом сумма моментов внешних сила равна нулю, то момент импульса системы сохраняется:
Слайд 30Частные случаи закона сохранения момента импульса незамкнутой системы частиц
Пример. Летевшая
горизонтально пуля со скоростью v0 массой m застревает в небольшом
деревянном шаре массой M, подвешенном на вертикальном стержне, который может свободно вращаться вокруг горизонтальной оси, проходящей через точку подвеса O.На пулю и шар действуют внешние силы mg, Mg и N (сила N в момент удара пули может быть очень большой). Однако, если за время удара стержень не успевает значительно отклониться, то моменты всех внешних сил относительно точки O равны нулю (линии действия этих сил проходят через точку O), то момент импульса системы сохраняется:
Слайд 31Частные случаи закона сохранения момента импульса незамкнутой системы частиц
2. Если
проекция на некоторую неподвижную ось Z момента всех внешних сил
равна нулю, то в проекции на ось Z момент импульса Lz сохраняется:
Слайд 32Частные случаи закона сохранения момента импульса незамкнутой системы частиц
Пример. Подвешенный
на нити шарик вращается с постоянной скоростью в горизонтальной плоскости
по окружности. В этом случае проекция на проходящую через точку подвеса O вертикальную ось Z момента импульса шарика сохраняется в процессе движения.Действительно, на шарик действуют: сила натяжения нити T (не создающая момента, т.к. линия ее действия проходит через точку O); сила тяжести, момент которой M = [r×mg] в проекции на ось Z равен нулю (см. рисунок). Поэтому Lz = const.
Вектор L имеет постоянную длину и вращается в пространстве вместе с шариком, описывая поверхность кругового конуса, в то время как его проекция на ось Z остается постоянной.
Слайд 33Частные случаи закона сохранения момента импульса незамкнутой системы частиц
3. Момент
импульса системы приблизительно сохраняется, если момент Mвнеш ограниченной по модулю
внешней силы действует в течение короткого промежутка времени Δt (т.е. Δt ≈ 0):