Дискретная математика

Содержание

1. Дискретная математика
2. Правило суммыКлассическая формулировкаЕсли элемент α можно выбрать
3. Теорема о мощности объединения множеств (современная формулировка)Количество
4. Причем, если множества не пересекаются, то теорема приобретает вид, аналогичный классической формулировке:
5. Для трех множеств теорема имеет вид:
6. Пример: Из 35 учащихся класс по итогам
7. Правило произведенияКлассическая формулировкаЕсли элемент α можно выбрать
8. Теорема о мощности прямого произведения множеств (современная формулировка)
9. Пример: Из 3 экземпляров учебника алгебры, 7
10. Пример: Из 10 арабских цифр составляют 5-значный
11. Число размещений без повторенийЧисло размещений без повторений
12. Число размещений с повторениямиЧисло размещений с повторениями
13. Число перестановок без повторенийЧисло перестановок без повторений
14. Задача на рассадки и расстановкиВ задачах на
15. ПримерСколькими способами можно расставить на книжной полке
16. Замечание: где – число
17. Схема расстановки:
18. Число сочетаний без повторенийЧисло сочетаний без повторений
19. Свойства1)
20. Урновая задачаУрновая задача – это задача, в
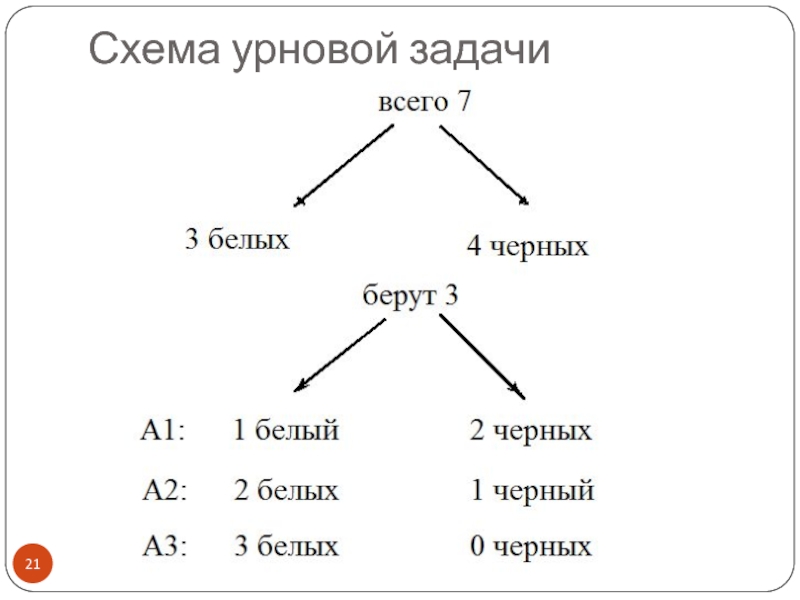
21. Схема урновой задачи
22. Общее число исходов эксперимента найдем по общей формуле
23. Количество элементов множества А1 найдем по формуле:
24. Количество элементов множества А2 найдем по формуле:
25. Количество элементов множества А3 найдем по формуле:
26. Выучить или переписать в тетрадь определения на слайдах2-5, 7, 8, 11-14, 16, 18, 19, 21
27. Скачать презентанцию

Правило суммыКлассическая формулировкаЕсли элемент α можно выбрать k способами, а элемент β можно выбрать m способами.Тогда или можно выбрать k +m способами.

Главная
Разное
Дискретная математика

Слайды и текст этой презентации

Слайд 1Комбинаторика

Дискретная математика

Слайд 2Правило суммы
Классическая формулировка
Если элемент α можно выбрать k способами, а

элемент β можно выбрать m способами.
Тогда или можно выбрать k

+m способами.

Слайд 3Теорема о мощности объединения множеств (современная формулировка)
Количество элементов объединения двух

множеств равно сумме количества элементов в первом и во втором

множестве, за вычетом количества элементов их пересечения:

Теорема о мощности объединения множеств (современная формулировка)Количество элементов объединения двух множеств равно сумме количества элементов в первом

Слайд 4Причем, если множества не пересекаются, то теорема приобретает вид, аналогичный

классической формулировке:

Слайд 5Для трех множеств теорема имеет вид:

Слайд 6Пример: Из 35 учащихся класс по итогам года имели “5”

по математике – 14 человек; по физике – 15 человек;

по химии – 18 человек; по математике и физике – 7 человек; по математике и химии – 9 человек; по физике и химии – 6 человек; по всем трем предметам – 4 человек.
Сколько человек имеют “5” по указанным предметам? Сколько человек не имеет “5” по указанным предметам? Имеет “5” только по математике? Имеет “5” только по двум предметам?

Пример: Из 35 учащихся класс по итогам года имели “5” по математике – 14 человек; по физике

Слайд 7Правило произведения
Классическая формулировка
Если элемент α можно выбрать k способами, а

элемент β можно выбрать m способами.
Тогда пару α и β

можно выбрать km способами.

Правило произведенияКлассическая формулировкаЕсли элемент α можно выбрать k способами, а элемент β можно выбрать m способами.Тогда пару

Слайд 8Теорема о мощности прямого произведения множеств (современная формулировка)

Слайд 9Пример:
Из 3 экземпляров учебника алгебры, 7 экземпляров учебника геометрии

и 6 экземпляров учебника физики, надо выбрать комплект, содержащий все

учебники по одному разу. Сколькими способами это можно сделать?

Пример: Из 3 экземпляров учебника алгебры, 7 экземпляров учебника геометрии и 6 экземпляров учебника физики, надо выбрать

Слайд 10Пример:
Из 10 арабских цифр составляют 5-значный код. Сколькими способами

это можно сделать так, чтобы: а) все цифры были разными;

б) на последнем месте четная цифра.

Пример: Из 10 арабских цифр составляют 5-значный код. Сколькими способами это можно сделать так, чтобы: а) все

Слайд 11Число размещений без повторений
Число размещений без повторений из n по

k – это число способов, сколькими можно из n различных

элементов построить векторов с k различными координатами.
Число размещений без повторений находится по формуле:

Пример: Сколькими способами можно построить 3-значное число с различными цифрами, не содержащее цифры 0?

Число размещений без повторенийЧисло размещений без повторений из n по k – это число способов, сколькими можно

Слайд 12Число размещений с повторениями
Число размещений с повторениями из n по

k – это число способов, сколькими можно из n различных

элементов построить векторов с k координатами, среди которых могут быть одинаковые.
Число размещений с повторениями находится по формуле:

Пример: Сколько слов длины 6 можно составить из 26 букв латинского алфавита?

Число размещений с повторениямиЧисло размещений с повторениями из n по k – это число способов, сколькими можно

Слайд 13Число перестановок без повторений
Число перестановок без повторений из n элементов

– это число способов, сколькими можно расположить на n различных

местах n различных элементов.
Число перестановок без повторений находится по формуле:

Число перестановок без повторенийЧисло перестановок без повторений из n элементов – это число способов, сколькими можно расположить

Слайд 14Задача на рассадки и расстановки
В задачах на рассадки и расстановки

используется тот факт, что

n элементов на n местах можно расставить

n! различными способами

Задача на рассадки и расстановкиВ задачах на рассадки и расстановки используется тот факт, чтоn элементов на n

Слайд 15Пример
Сколькими способами можно расставить на книжной полке 5 различных книг?

В скольких случаях две определенные книги А и В окажутся

рядом?
Всего вариантов расстановки 5 книг на 5 местах :
5!=120

ПримерСколькими способами можно расставить на книжной полке 5 различных книг? В скольких случаях две определенные книги А

Слайд 16Замечание:

где – число способов выбрать нужные

места;
– число способов расположить на них

нужные элементы;
– число способов расположить остальные элементы на оставшихся местах.

Замечание: где – число способов выбрать нужные места; – число способов

Слайд 17Схема расстановки:

Слайд 18Число сочетаний без повторений
Число сочетаний без повторений из n по

k – это число способов, сколькими можно из n различных

элементов выбрать k штук без учета порядка.
Число сочетаний без повторений находится по формуле:

Число сочетаний без повторенийЧисло сочетаний без повторений из n по k – это число способов, сколькими можно

Слайд 19Свойства
1)

2)

3) 4)

5)

6) 7)

Слайд 20Урновая задача
Урновая задача – это задача, в которой производится выбор

сразу нескольких элементов из заданной совокупности.

Пример: В урне 7 шаров.

Из них 3 белых, 4 черных. Наугад выбирают 3 шара. Сколькими способами это можно сделать? В скольких случаях среди них будет: 1) один белый; 2) два белых; 3) все белые.

Урновая задачаУрновая задача – это задача, в которой производится выбор сразу нескольких элементов из заданной совокупности.Пример: В

Слайд 21Схема урновой задачи

Слайд 22Общее число исходов эксперимента найдем по общей формуле

Слайд 23Количество элементов множества А1 найдем по формуле:

Слайд 24Количество элементов множества А2 найдем по формуле:

Слайд 25Количество элементов множества А3 найдем по формуле:

Слайд 26Выучить или переписать в тетрадь определения на слайдах
2-5, 7, 8,

11-14, 16, 18, 19, 21

Скачать презентацию

Разделы презентаций

Дискретная математика

Содержание

Слайды и текст этой презентации

Слайд 1КомбинаторикаДискретная математика

Слайд 2Правило суммыКлассическая формулировкаЕсли элемент α можно выбрать k способами, а

элемент β можно выбрать m способами.Тогда или можно выбрать k

Слайд 3Теорема о мощности объединения множеств (современная формулировка)Количество элементов объединения двух

множеств равно сумме количества элементов в первом и во втором

Слайд 4Причем, если множества не пересекаются, то теорема приобретает вид, аналогичный

классической формулировке:

Слайд 5Для трех множеств теорема имеет вид:

Слайд 6Пример: Из 35 учащихся класс по итогам года имели “5”

по математике – 14 человек; по физике – 15 человек;

Слайд 7Правило произведенияКлассическая формулировкаЕсли элемент α можно выбрать k способами, а

элемент β можно выбрать m способами.Тогда пару α и β

Слайд 8Теорема о мощности прямого произведения множеств (современная формулировка)

Слайд 9Пример: Из 3 экземпляров учебника алгебры, 7 экземпляров учебника геометрии

и 6 экземпляров учебника физики, надо выбрать комплект, содержащий все

Слайд 10Пример: Из 10 арабских цифр составляют 5-значный код. Сколькими способами

это можно сделать так, чтобы: а) все цифры были разными;

Слайд 11Число размещений без повторенийЧисло размещений без повторений из n по

k – это число способов, сколькими можно из n различных

Слайд 12Число размещений с повторениямиЧисло размещений с повторениями из n по

k – это число способов, сколькими можно из n различных

Слайд 13Число перестановок без повторенийЧисло перестановок без повторений из n элементов

– это число способов, сколькими можно расположить на n различных

Слайд 14Задача на рассадки и расстановкиВ задачах на рассадки и расстановки

используется тот факт, чтоn элементов на n местах можно расставить

Слайд 15ПримерСколькими способами можно расставить на книжной полке 5 различных книг?

В скольких случаях две определенные книги А и В окажутся

Слайд 16Замечание: где – число способов выбрать нужные

места; – число способов расположить на них

Слайд 17Схема расстановки:

Слайд 18Число сочетаний без повторенийЧисло сочетаний без повторений из n по

k – это число способов, сколькими можно из n различных

Слайд 19Свойства1)

Слайд 20Урновая задачаУрновая задача – это задача, в которой производится выбор

сразу нескольких элементов из заданной совокупности.Пример: В урне 7 шаров.

Слайд 21Схема урновой задачи

Слайд 22Общее число исходов эксперимента найдем по общей формуле

Слайд 23Количество элементов множества А1 найдем по формуле:

Слайд 24Количество элементов множества А2 найдем по формуле:

Слайд 25Количество элементов множества А3 найдем по формуле:

Слайд 26Выучить или переписать в тетрадь определения на слайдах2-5, 7, 8,

11-14, 16, 18, 19, 21

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Комбинаторика

Дискретная математика

Слайд 2Правило суммы
Классическая формулировка
Если элемент α можно выбрать k способами, а

элемент β можно выбрать m способами.
Тогда или можно выбрать k

Слайд 3Теорема о мощности объединения множеств (современная формулировка)
Количество элементов объединения двух

Слайд 7Правило произведения
Классическая формулировка
Если элемент α можно выбрать k способами, а

элемент β можно выбрать m способами.
Тогда пару α и β

Слайд 9Пример:
Из 3 экземпляров учебника алгебры, 7 экземпляров учебника геометрии

Слайд 10Пример:
Из 10 арабских цифр составляют 5-значный код. Сколькими способами

Слайд 11Число размещений без повторений
Число размещений без повторений из n по

Слайд 12Число размещений с повторениями
Число размещений с повторениями из n по

Слайд 13Число перестановок без повторений
Число перестановок без повторений из n элементов

Слайд 14Задача на рассадки и расстановки
В задачах на рассадки и расстановки

используется тот факт, что

n элементов на n местах можно расставить

Слайд 15Пример
Сколькими способами можно расставить на книжной полке 5 различных книг?

Слайд 16Замечание:

где – число способов выбрать нужные

места;
– число способов расположить на них

Слайд 18Число сочетаний без повторений
Число сочетаний без повторений из n по

Слайд 19Свойства
1)

Слайд 20Урновая задача
Урновая задача – это задача, в которой производится выбор

сразу нескольких элементов из заданной совокупности.

Пример: В урне 7 шаров.

Слайд 26Выучить или переписать в тетрадь определения на слайдах
2-5, 7, 8,