Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дискретная математика
Содержание
- 1. Дискретная математика
- 2. ВведениеСети – это графы, которые моделируют реальные транспортные и коммуникационные сети.
- 3. ВведениеЗадача о максимальном потоке в сети заключается
- 4. ВведениеПод объектами могут пониматься - пакеты данных,
- 5. ВведениеЭта задача может использоваться при составлении расписания
- 6. ВведениеПеремещение объектов могут ограничено пропускной способностью соединений сети или скоростью транспорта на загруженных дорогах.
- 7. ВведениеВ задаче о максимальном потоке одна их
- 8. СетиСетью называется частично ориентированный граф G(V, E)Истоком
- 9. СетиИсток - вершина, локальная степень захода которой
- 10. СетиЕсли в сети k истоков и m
- 11. СетиПусть s – исток, t – сток,
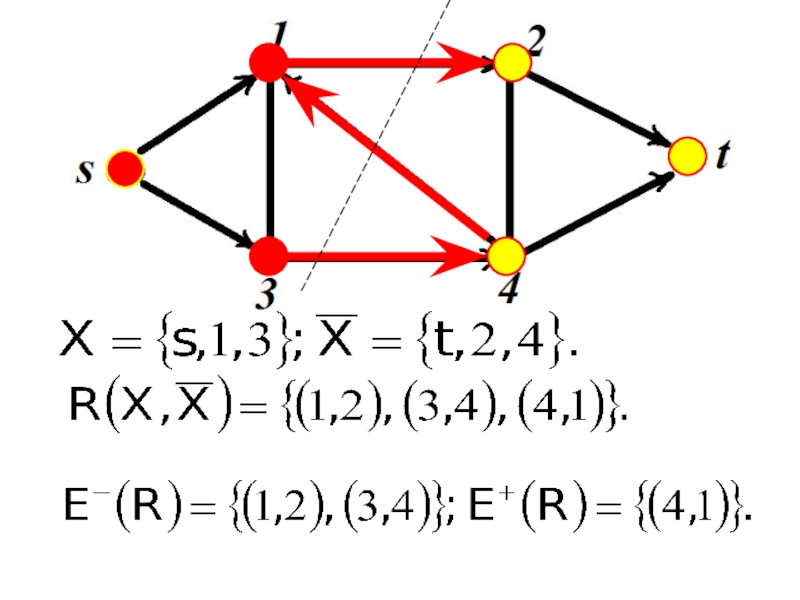
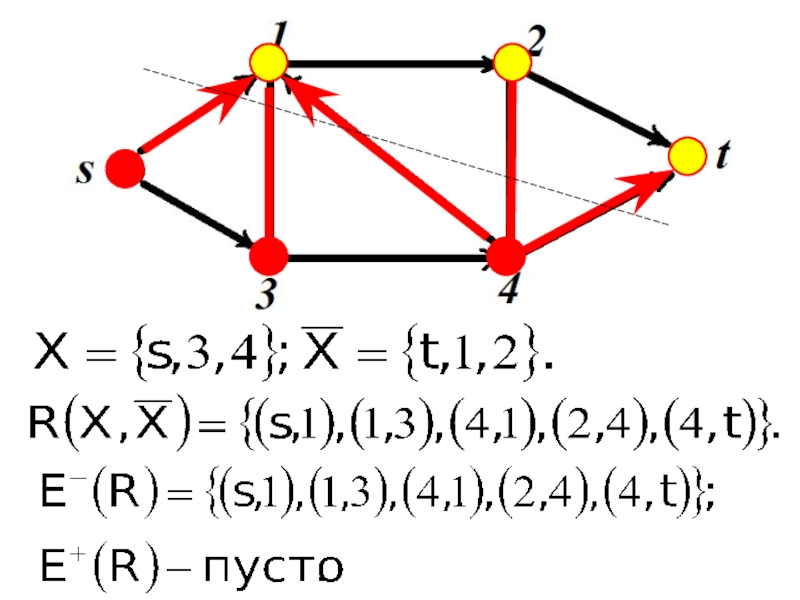
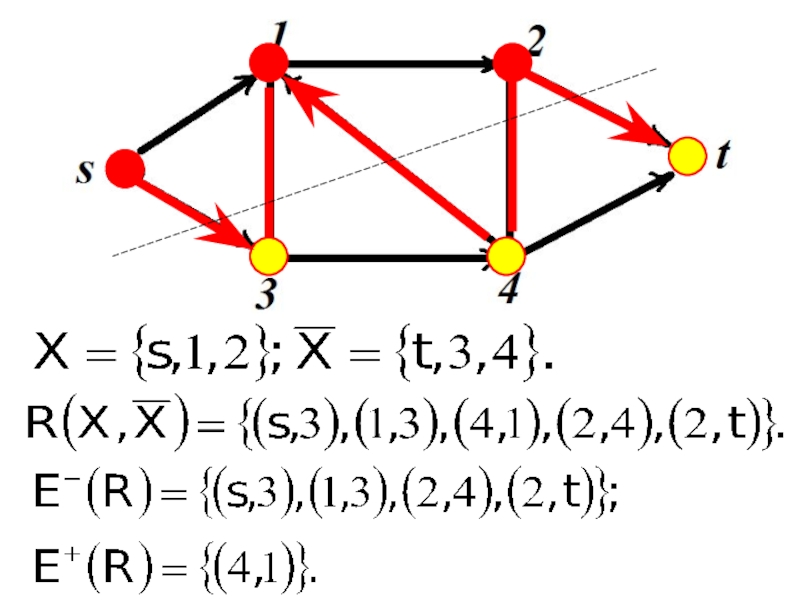
- 12. СетиРазобьем множество вершин V на два подмножества
- 13. СетиОриентированные ребра с началом в Х и концом в называются прямыми.Множество прямых ребер обозначим
- 14. СетиОриентированные ребра с началом в
- 15. СетиВсе неориентированные ребра являются прямыми.Их ориентация произвольна, и определяется при задании потока в сети.
- 16. СетиЗамечание 1:Прямым или обратным ребро будет в зависимости от вида разреза в сети.
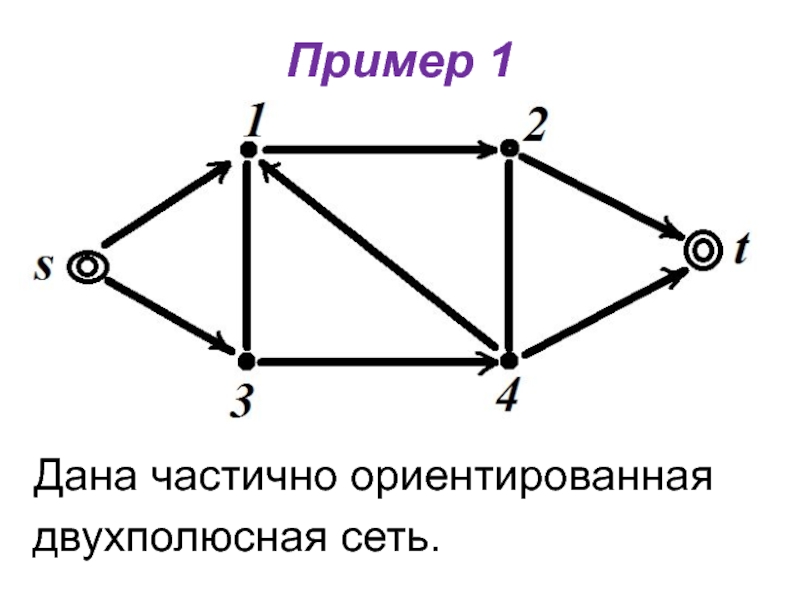
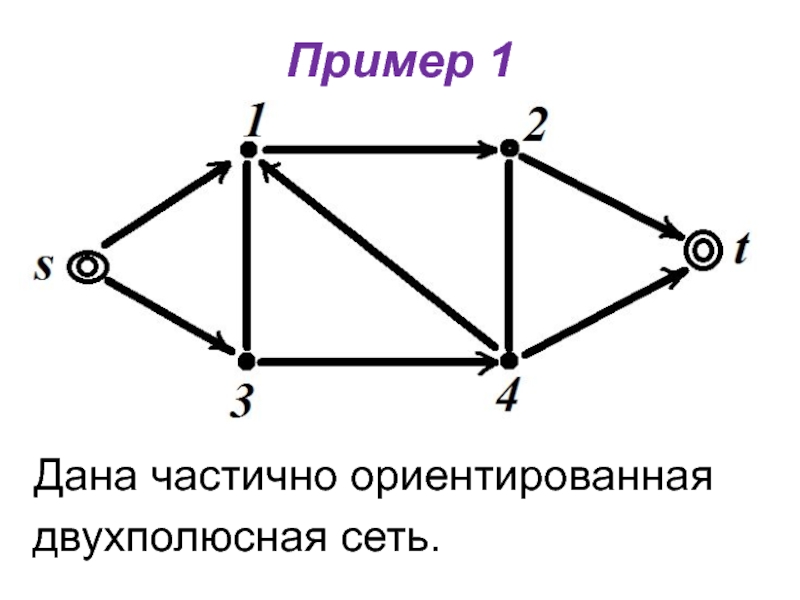
- 17. Пример 1Дана частично ориентированная двухполюсная сеть.
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Поток в сетиПусть S произвольная частично ориентированная
- 23. Поток в сетиПотоком в сети S называется
- 24. Поток в сетиФункция f удовлетворяет условиям:1)2) выполняется закон Киргофа:дивергенция любой внутренней вершины сети равна 0.
- 25. Поток в сетиДивергенция вершины сети – число находимое по формуле:
- 26. Поток в сетиВеличина потока в сети S – равна дивергенции потока в вершине s (дивергенция истока).
- 27. Поток в сетиЗамечание 2:
- 28. Поток в сетиЗамечание 3:Величина потока в сети есть величина переменная, зависящая от значений функции f(e).
- 29. Пример 1Дана частично ориентированная двухполюсная сеть.
- 30. Поток в сетиЗамечание 3:Величина потока в сети есть величина переменная, зависящая от значений функции f(e).
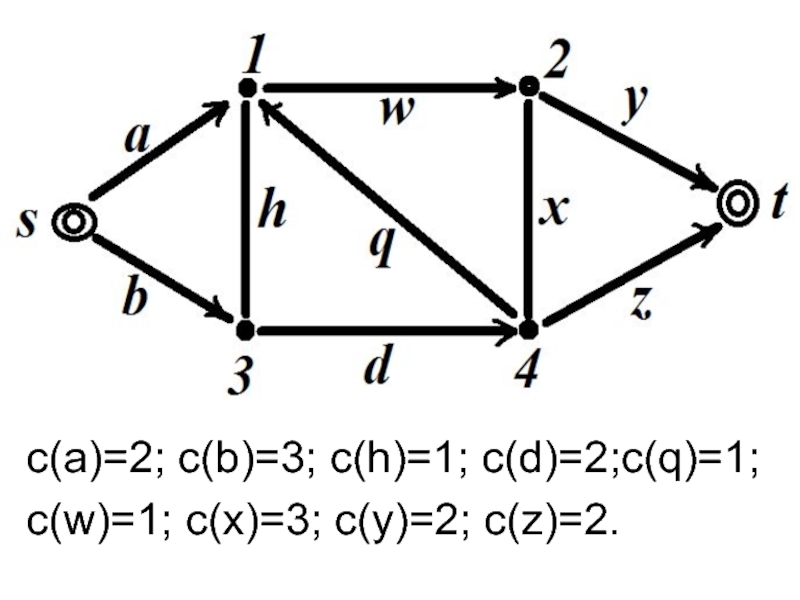
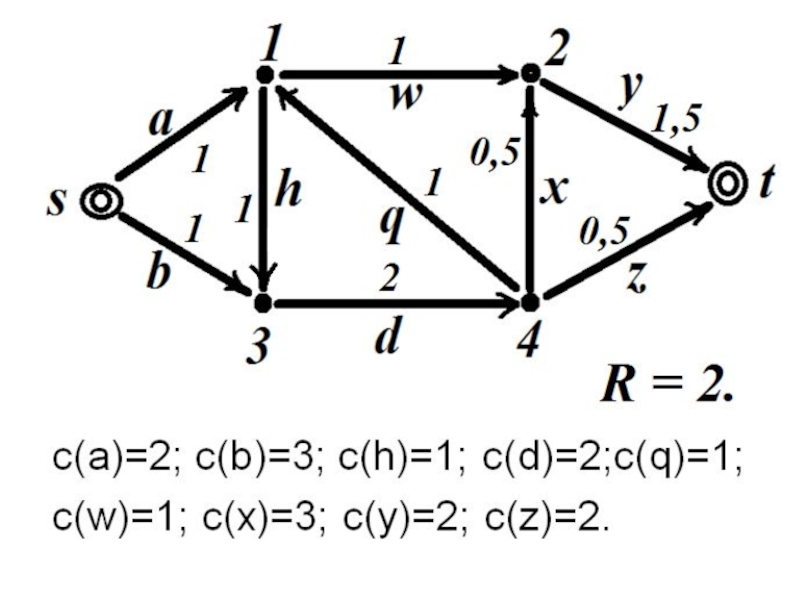
- 31. с(a)=2; c(b)=3; c(h)=1; c(d)=2;c(q)=1;c(w)=1; c(x)=3; c(y)=2; c(z)=2.
- 32. Слайд 32
- 33. Слайд 33
- 34. Поток в сетиКаждому ребру разреза R ставится
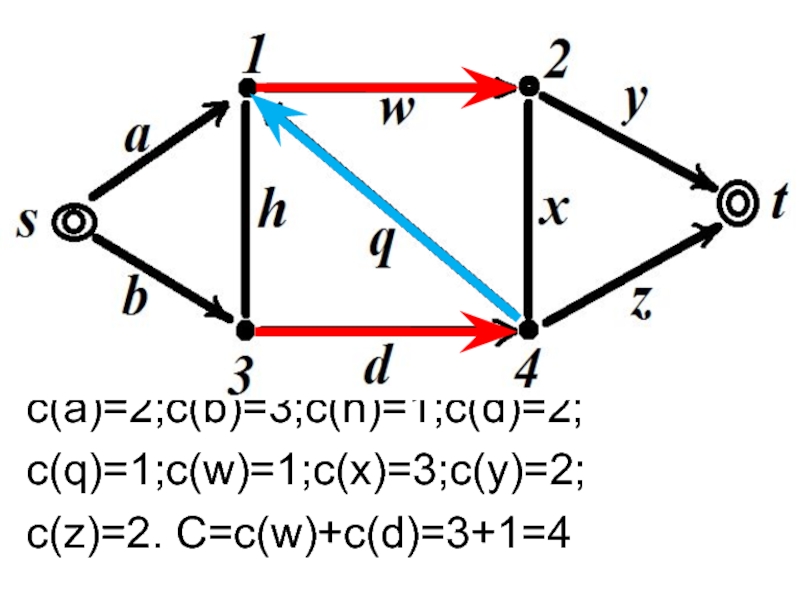
- 35. с(a)=2;c(b)=3;c(h)=1;c(d)=2;c(q)=1;c(w)=1;c(x)=3;c(y)=2;c(z)=2. C=c(w)+c(d)=3+1=4
- 36. C=c(b)+c(h)+c(x)+c(y)=3+1+3+2=9
- 37. Поток в сетиТеорема Форда-ФалкерсонаМаксимальная величина потока в
- 38. Скачать презентанцию
ВведениеСети – это графы, которые моделируют реальные транспортные и коммуникационные сети.
Слайды и текст этой презентации
Слайд 3Введение
Задача о максимальном потоке в сети заключается в том, чтобы
подсчитать максимальное количество некоторых объектов, которые могут двигаться от одного
конца сети к другому. При этом пропускная способность узлов сети ограничена.
Слайд 4Введение
Под объектами могут пониматься - пакеты данных, путешествующих по интернету;
-
коробки с товарами, которые везут по автомагистрали; и т. д.
Слайд 5Введение
Эта задача может использоваться при составлении расписания авиарейсов, распределения задач
в суперкомпьютерах, обработке цифровых изображений и расположении последовательности ДНК.
Слайд 6Введение
Перемещение объектов могут ограничено пропускной способностью соединений сети или скоростью
транспорта на загруженных дорогах.
Слайд 7Введение
В задаче о максимальном потоке одна их вершин графа назначается
истоком – точкой, в которой все объекты начинают свой путь,
а другая – стоком, точкой, в которую они все направляются. Пропускная способ-ность каждого ребра ограничена. В вершинах вещество не накапливается – сколько пришло, столько и ушло.
Слайд 8Сети
Сетью называется частично ориентированный граф G(V, E)
Истоком и стоком (входным
и выходным полюсом) называются некоторые отмеченные вершины.
Слайд 9Сети
Исток - вершина, локальная степень захода которой равна 0.
Сток –
вершина, локальная степень исхода которой равна 0.
Слайд 10Сети
Если в сети k истоков и
m стоков –
сеть называется (k,m)- полюсником.
Если в сети 1 исток и 1
сток, сеть называется двухполюсной.Далее будем рассматривать только двухполюсные сети.
Слайд 11Сети
Пусть s – исток, t – сток, так что любая
другая вершина лежит на пути из вершины s в t.
Вершины, не являющиеся истоком и стоком называются внутренними вершинами сети.
Слайд 12Сети
Разобьем множество вершин V на два подмножества Х и
таких, что , а
.Множество ребер, реализующих это разбиение назовем разрезом
Слайд 13Сети
Ориентированные ребра с началом в Х и концом в
называются
прямыми.
Множество прямых ребер обозначим
Слайд 14Сети
Ориентированные ребра с началом в и концом в
Х
называются обратными.
Множество обратных ребер обозначим
Слайд 15Сети
Все неориентированные ребра являются прямыми.
Их ориентация произвольна,
и определяется при
задании потока в сети.
Слайд 22Поток в сети
Пусть S произвольная частично ориентированная сеть.
Пусть каждому
ребру сети приписано число
пропускная способность ребра е
Слайд 23Поток в сети
Потоком в сети S называется пара, составленная из
числовой и нечисловой функций (f ,w):
w – ориентация всех
неориентированных ребер сети,f =f(e) – функция значений потока на ребрах.
Слайд 24Поток в сети
Функция f удовлетворяет условиям:
1)
2) выполняется закон Киргофа:
дивергенция любой
внутренней вершины сети равна 0.
Слайд 26Поток в сети
Величина потока в сети S – равна дивергенции
потока в вершине s (дивергенция истока).
Слайд 28Поток в сети
Замечание 3:
Величина потока в сети есть величина переменная,
зависящая от значений функции f(e).
Слайд 30Поток в сети
Замечание 3:
Величина потока в сети есть величина переменная,
зависящая от значений функции f(e).
Слайд 34Поток в сети
Каждому ребру разреза R ставится в соответствие пропускная
способность разреза с(R), равная сумме пропускных способностей всех прямых ребер
разреза.
Слайд 37Поток в сети
Теорема Форда-Фалкерсона
Максимальная величина потока в сети S равна
минимальной пропускной способности среди всех ее разрезов.
