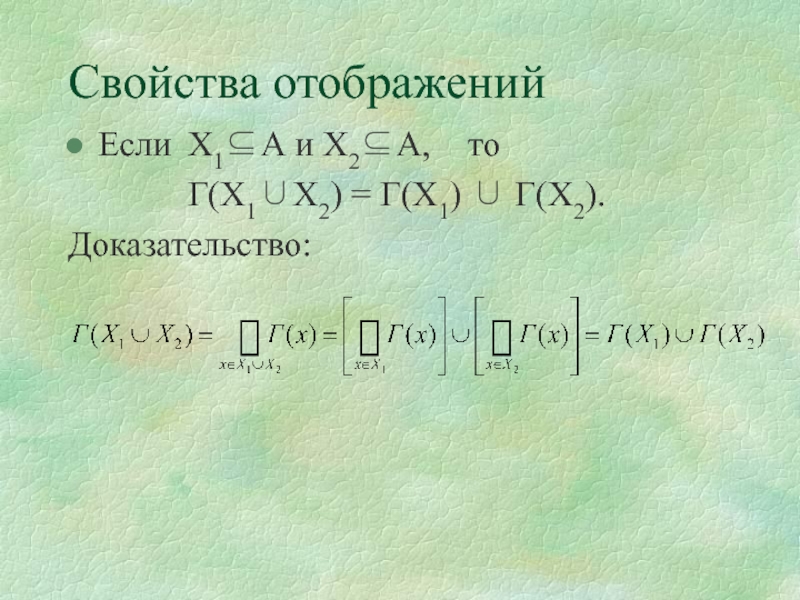Слайд 1Дискретный анализ
Теория множеств
Логика
Теория графов
Слайд 2Литература
Общая
1. Новиков Ф.А. Дискретная математика для программистов. 2000, 304
с.
2. Донской В. И. Дискретная математика. 2000.
3. Яблонский С.
В. Введение в дискретную математику. Серия: Высшая математика. М.: Высшая школа. 2000
4. Москинова Г. И. Дискретная математика. Математика для менеджеров в примерах и упражнениях: Учебное пособие. М.: ИК Логос. 2000.
5. Акимов О. Е. Дискретная математика. Логика, группы, графы. Серия: Технический университет. М.: Лаборатория Базовых Знаний. 2001.
6. Иванов Б. Н. Дискретная математика. Алгоритмы и программы. Серия: Технический университет. М.: Лаборатория Базовых Знаний. 2001 г, 285 с.
Слайд 3Литература
Теория множеств
1. Коршунов Ю.М. Математические основы кибернетики. Учебное пособие
для втузов. М.: Энергия. 1972, 376 с.
2. Кузнецов О.П., Адельсон-Вельский
Г.М. Дискретная математика для инженера. М.: Энергоатомиздат, 1988. 480 с.
3. Основы кибернетики. Математические основы кибернетики. Под ред. проф. К.А.Пупкова. М: Высшая школа. 1974. 413 с.
Слайд 4Литература
Логика
4. Бочаров В.А., Маркин В.И. Основы логики. 1997.
5.
Савельев А.Я. Арифметические и логические основы цифровых автоматов: Учебник. -
М.: Высш. школа, 1980. - 255 с., ил.
6. Савельев А.Я. Прикладная теория цифровых автоматов: Учебник. - М.: Высш. школа, 1989. - 273 с., ил.
Теория автоматов / Ю.Г.Карпов - СПб.: Питер, 2002. - 224 с.
Слайд 5Литература
Теория графов
7. Зыков А.А. Основы теории графов. 1987. 384
с.
8. Оре О. Теория графов. М: Наука, 1980. 336с
9.
Цой С., Цхай С.М. Прикладная теория графов. Алма-Ата: Наука, 1971.500 c.
10. Лекции по теории графов / Емеличев В.А. и др. - М.: Наука, 1990. - 384 с.
Слайд 6Теория множеств
Множества
Операции над множествами
Упорядоченные множества
Соответствия
Отображения
и функции
Отношения
Слайд 7Множества. Основные понятия
Множество - совокупность определенных, вполне различаемых объектов, рассматриваемых
как целое.
Элемент множества - отдельный объект множества.
Пустое множество -
множество не содержащее элементов.
Универсальное множество (универсум) U - множество содержащее все возможные элементы в рамках заданного рассмотрения
Мощность множества |M| - количество элементов множества
Слайд 8Способы задания множеств
Перечисление элементов
М = {a1, a2, a3, …,
ak}
M9 = {1, 2, 3, 4, 5, 6, 7, 8,
9}
Выделение определяющего свойства
M = {x | P(x)}
M9 = {n | n & n < 10}
Определение порождающей процедуры
M = {x | x = f}
M9 = {n | for n from 1 to 9 write n}
Слайд 9Парадокс Рассела
Множество всех множеств,
не содержащих себя в
качестве элемента:
Y = {X | X X}
Если множество Y
существует, то YY ?
Пусть YY , тогда YY (по определению).
Пусть YY, тогда YY (по определению).
Получаем логическое противоречие.
Пути устранения этого противоречия:
Вид характеристического предиката: P(x) = xA & Q(x) = { xA | Q(x)} (для Y универсум не задан, Y - не множество)
Теория типов. Объекты имеют тип 0, множества -1, множества множеств - 2 и т.д. (Y - не имеет типа, Y - не множество)
Функция вычисления элементов множества. (способ вычисления XX не задан, Y - не множество )
Слайд 10Сравнение множеств
Два множества равны между собой, если они состоят
из одних и тех же элементов
Свойства: для любых трех множеств
X, Y, Z верно
рефлексивность X = X; (идемпотентность)
коммутативность X = Y Y = X;
транзитивность (X = Y) & (Y = Z) X = Z.
Множество X является подмножеством множества Y, если любой элемент множества X принадлежит и множеству Y.
XY, если xX и xY; XY, если XY и XY
Свойства:
рефлексивность X X
транзитивность XY & Y Z, XZ
свойства 0 и 1 YU
Слайд 11Границы множества
Если множество конечно и состоит из элементов, сравнимых
между собой, то существуют наибольший и наименьший элементы такого множества.
Если множество бесконечно и состоит из элементов, сравнимых между собой, то существуют границы этого множества: верхняя и нижняя.
S = {xR| a a = inf S ('инфинум)
b = sup S (супр'емум)
Слайд 12Теорема о границах
Если ВА, то inf В inf
А; sup В sup А.
Доказательство:
Пусть b'B и b' =
inf B; т.к. ВА b'А.
Пусть a'A и a' = inf A; при этом если a' = b', то b' = a'=inf А; а если a' b', то b' = inf B > a'=inf А.
Пусть b"B и b" = sup B; т.к. ВА b"А.
Пусть a"A и a" = sup A; при этом если b" = a", то a"=sup А = b"=sup B; а если b" a", то a"=sup А > b".
A
B
a'
b'
b"
a"
Слайд 13Операции над множествами
Объединение AB = {x |xA xB}
Пересечение AB = {x
|xA & xB}
Разность A\B = {x |xA & xB}
Симметрическая разность
A/B =
(AB)\(AB ) = {x | (xA & xB) (xA & xB)}
Дополнение = {x | x A} = U\A, где U - некоторый универсум.
Слайд 14Объединение
Объединением множеств А и В называется множество, состоящее из всех
тех и только тех элементов, которые принадлежат хотя бы одному
из множеств А или В.
Свойства
рефлексивность А А = A
коммутативность А В = В А
ассоциативность А (ВС) = (АВ) С = А В С
свойство 0 А = А
свойство 1 А U = U
А
В
Слайд 15Пересечение
Пересечением множеств А и В называется множество, состоящее из всех
тех и только тех элементов, которые принадлежат как множеству А,
так и множеству В.
Свойства
рефлексивность А А = A
коммутативность А В = В А
ассоциативность А (ВС) = (АВ) С = А В С
свойство 0 А =
свойство 1 А U = А
А
В
АВ
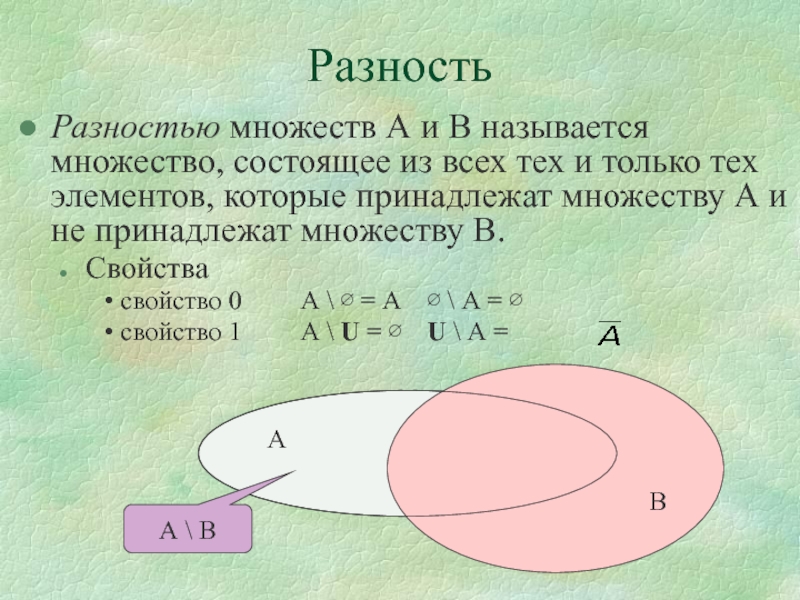
Слайд 16Разность
Разностью множеств А и В называется множество, состоящее из всех
тех и только тех элементов, которые принадлежат множеству А и
не принадлежат множеству В.
Свойства
свойство 0 А \ = А \ А =
свойство 1 А \ U = U \ А =
А
В
А \ В
Слайд 17Симметрическая разность
Симметрической разностью множеств А и В называется множество, состоящее
из всех тех и только тех элементов, которые принадлежат объединению
множеств А и В, и не принадлежат их пересечению.
Свойства
коммутативность А / В = В / А
ассоциативность А / (В/С) = (А/В) / С = А / В / С
свойство 0 А / = А
свойство 1 А / U =
А
В
Слайд 18Дополнение
Дополнением множества А до универсального множества называется множество, состоящее из
всех тех и только тех элементов, которые принадлежат универсальному множеству,
и не принадлежат множеству А.
Свойства
А = U А =
инволютивность = А
U
A
Слайд 19Разбиения и покрытия
Система множеств X={X1, X2, …,Xn} называется разбиением множества
М, если она удовлетворяет условиям:
любое множество системы есть подмножество множества
М: XiX : XiM, 1in;
любые два множества системы являются непересекающимися: XiX, XjX : ij XiXj=
объединение всех множеств системы дает множество М:
Слайд 20Булеан
Множество всех подмножеств множества М называется булеаном и обозначается 2М:
2М = {A | A M}
M = {a, b,
c}
2M = {, {a}, {b}, {c}, {a, b}, {a, c}, {b, c},{a, b, c}}
M1 = {{c}, {a, c}, {b, c},{a, b, c}}
M2 = {, {a}, {b}, {a, b}}
Слайд 21Теорема
Для конечного множества М |2M| = 2|M|.
Доказательство:
Если |M|=0, то
М= и 2 = {}. |2|= |{}| =1 = 20
=2||.
Пусть для любого множества М |M|Рассмотрим М={a1, a2, …,ak}, |M|=k.
Положим, М1={X2M| akX} и М2={X2M| akX}.
Имеем 2M = М1М2 и М1М2 = .
|M1|=2k-1, |M2|=2k-1
|2M|=|M1|+|M2|=2k-1+2k-1=22k-1=2k = 2|M|
Слайд 22Алгебра подмножеств
Алгебра =
Результат применения любой операции к
элементам базового множества также является элементом базового множества
Алгебра подмножеств
AM =
<2U, {, ,\, }>
Множество всех подмножеств универсума с операциями объединения, пересечения , разности и дополнения образует алгебру подмножеств множества U.
Слайд 23Законы теории множеств
Дистрибутивный
A (B C) = (A
B) (A C)
A (B C) =
(A B) (A C)
Закон поглощения
(A B) A = A (A B) A = A
Законы де Моргана
Выражение для разности
A \ B = A
Слайд 24Метод доказательства законов алгебры подмножеств
Обозначим алгебраическое выражение над множествами А,
В, С как Е(А,В,С). Результат выполнения операций данного выражения есть
некоторое множество Е.
Пусть Е1 и Е2 два выражения над А,В,С.
Чтобы доказать, что Е1=Е2, достаточно показать, что Е1Е2 и Е2Е1.
Чтобы доказать, что Е1Е2, нужно убедиться, что из хЕ1 следует хЕ2; и, аналогично, для Е2Е1 – что из хЕ2 хЕ1.
Слайд 25U
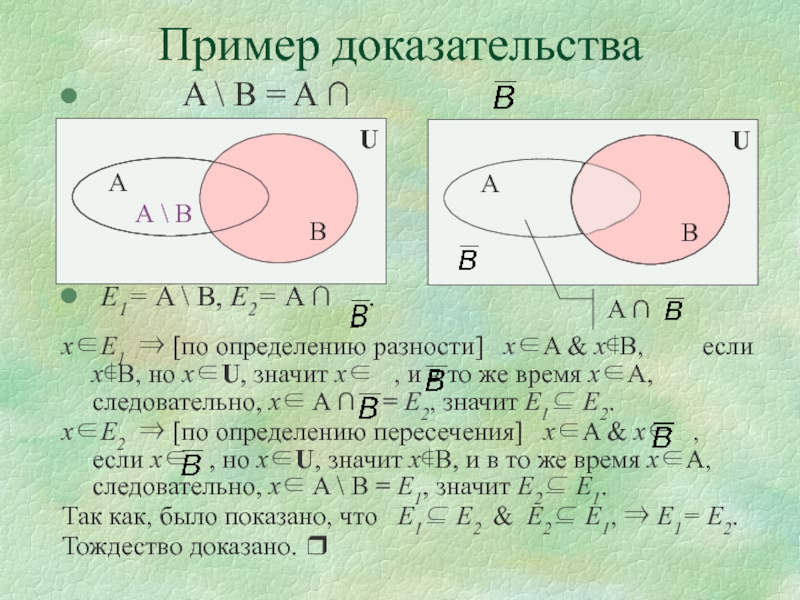
Пример доказательства
A \ B = A
E1= A
\ B, E2= A .
xE1
[по определению разности] xA & xB, если xB, но xU, значит x , и в то же время xA, следовательно, x A = E2, значит E1 E2.
xE2 [по определению пересечения] xA & x , если x , но xU, значит xB, и в то же время xA, следовательно, x A \ В = E1, значит E2 E1.
Так как, было показано, что E1 E2 & E2 E1, E1= E2.
Тождество доказано.
А
А \ В
В
U
В
А
В
A
Слайд 26Структурированное множество
Кортеж - последовательность элементов, или совокупность элементов, в которой
каждый элемент занимает определенное место.
Элементы данной совокупности называются компонентами кортежа.
Обозначение:
(а1,
а2, …, аn) - кортеж длины n с компонентами а1, …, аn.
( ) = - пустой кортеж.
Примеры:
множество слов во фразе;
(x,y) - координаты точки на плоскости;
запись в таблице базы данных.
Отличие от обычного множества: кортеж может содержать одинаковые по значению компоненты, например, точка с координатой (5,5).
Слайд 27Вектор. Гиперпространство.
Вектор (точка пространства) - кортеж, элементами которого являются вещественные
числа.
Пространство, определяемое n-мерными векторами, называют n-мерным пространством (пространством n измерений)
или гиперпространством.
Слайд 28Проекция вектора
Если кортеж (а1,а2) рассматривать как вектор, проведенный из начала
координат в данную точку (а1,а2), то компоненты а1, а2 будут
проекциями вектора на оси координат.
ПрХ(а1,а2) = а1.
ПрY(а1,а2) = а2.
Если а = (а1, а2, …,аn) - вектор гиперпространства, то Прi a = аi, i= 1, 2, …,n;
Прi,j,…,k a = (аi, аj, …, аk), где i, j, …,k номера осей, такие что, 1 i < j < … < k n;
Пр a = .
Слайд 29Прямое произведение множеств
Прямым (декартовым) произведением множеств А и В, называется
множество АВ, состоящее из всех тех и только тех упорядоченных
пар, первая компонента которых принадлежит множеству А, вторая - В.
АВ = {(a,b) | aA & bB}.
А1А2...Аn = {(a1,a2,…,an) | aiAi , i=1, 2, …, n}.
Свойства:
декартово произведение не коммутативно:
АВ BA.
декартово произведение есть пустое множество, если один из сомножителей - пустое множество:
АВ = A= B= .
Слайд 30Степень множества
Степенью множества А называется его прямое произведение самого на
себя: Аn = AA... A.
Соответственно,
А0 = {}; А1
= A; А2 = AA; Аn = AAn-1.
Теорема: |A B| = |A||B|.
Доказательство:
1-й компонент кортежа (а,b) можно выбрать |A| способами,
2-й компонент - |B| способами.
Таким образом, имеется всего |A||B| различных кортежей (a,b).
.
Следствие: | Аn | = |A|n.
Слайд 31Проекция множества
Пусть А - множество, состоящее из кортежей длины n,
тогда проекцией множества А называют множество проекций кортежей из А.
(операция
проекции может применяться только к таким множествам, элементами которых являются кортежи одинаковой длины).
Если А = XY, то Пр1А = Х, Пр2А = Y.
Если А XY, то Пр1А Х, Пр2А Y.
Слайд 32Соответствия
Соответствие - это множество пар вида (a,b), образующихся при
сопоставлении заданным образом элементов множества А элементам множества В, и
сами сопоставляемые множества А и В.
q = (A, B, Q), QAB.
ПрАQ A называется областью определения соответствия, или источником соответствия.
ПрВQ В называется областью значений соответствия, или приемником.
Множество пар Q, определяющих соответствие, называется графиком соответствия.
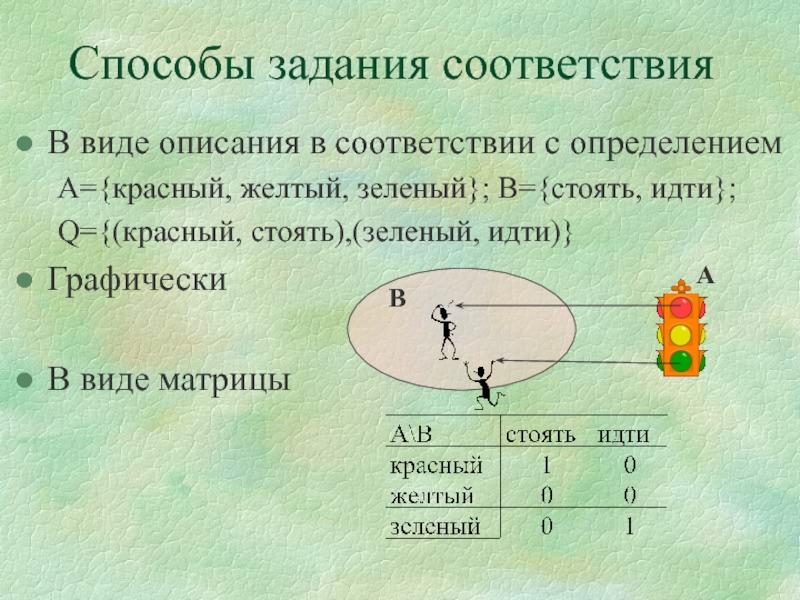
Слайд 33В виде описания в соответствии с определением
А={красный, желтый, зеленый}; B={стоять,
идти};
Q={(красный, стоять),(зеленый, идти)}
Графически
В виде матрицы
B
Способы задания соответствия
А
Слайд 34Обратное соответствие
Соответствие, обозначаемое как q-1 = (B, A,Q-1), где Q-1
BA, является обратным для соответствия q=(A,B,Q), где QAB, и получается,
если данное соответствие q рассматривать в обратном направлении.
Пример:
А={красный, желтый, зеленый}; B={стоять, идти};
Q={(красный, стоять),(зеленый, идти)}.
Q-1={(стоять, красный),(идти, зеленый)}.
Свойства:
(q-1)-1 = q.
Слайд 35Композиция соответствий
Композиция соответствий - это операция с 3-мя множествами А,
В, С, на которых заданы два соответствия q = (A,
B, Q), где QAB и р = (В, С, Р), где Р BC, причем область значений первого соответствия q совпадает с областью определения второго р Пр2Q = Пр1Р.
Обозначение:
q(p) = (A, C, QP), QP A C.
Слайд 36Ядро соответствия
Ядро соответствия q образует соответствие o, получаемое в результате
композиции прямого и обратного соответствия q: o =
q°q-1.
Пример:
M={a,b}; A = 2M = {, {a},{b},{a, b}}; B={0, 1, 2}.
q = (A, B, Q), Q = {(X,k) | XM & |X| = k}
q°q-1 = (A, A, O), O = {(,), ({a},{a}), ({a},{b}), ({b},{b}), ({a, b},{a, b})}
Слайд 37Отображения
Полностью определенное на множестве источнике соответствие q(A,B,Q) (где множество А
- есть область определения данного соответствия q) называется отображением множества
А в множество В.
Обозначения
Г: А В = (А,В,Г), где ГАВ, ПрАГ = А или (А,В,Г), ГАВ | aA bB
Каждому элементу xA отображение Г ставит в соответствие подмножество Г(x) В, которое называют образом элемента x.
Пусть XA; xX, Г(x)В – образ элемента х, тогда Г(Х) = – образ множества Х
Слайд 38Отображения
Отображение i : XX называется тождественным, если I(x) =
x для всех хХ, и обозначается как idX
или как 1Х.
Свойство: Для любого отображения Г : XY имеет место 1Y g = g 1X = g.
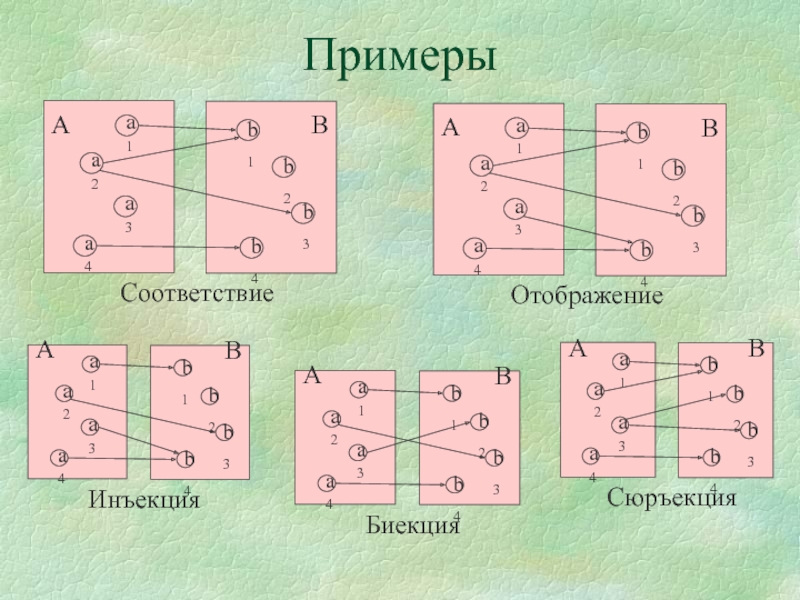
Отображение Г : XY называется инъекцией, если для любых 2-х x1,x2X из равенства Г(x1)=Г(x2) следует x1=x2.
Отображение Г : XY называется сюръекцией, если для каждого yY существует такой xX, что y=Г(x).
Отображение Г : XY называется биекцией, если оно одновременно является инъекцией и сюръекцией.
Слайд 40Свойства отображений
Если Х1А и Х2А, то
Г(Х1Х2) = Г(Х1)
Г(Х2).
Доказательство:
Слайд 41Свойства отображений
Если Х1А и Х2А, то
Г(Х1Х2) = Г(Х1)
Г(Х2) – верно только в случае однозначного отображения.
Доказательство:
Разобьем множества Х1
и Х2 на 2 мн-ва Х1=А0 А1 и Х2=А0 А2, где А0 = Х1Х2, А1=Х1\Х2, А2=Х2\Х1.
{А0, А1, А2} – есть разбиение множества Х1 Х2.
Слайд 42Частный случай отображения
Отображение вида Г: А А является частным
случаем отображения Г: А В, при А=В, представляет собой
отображение множества А в себя самого и определяется парой (А, Г), где ГА2.
Композицией 2-х отображений вида Г:АА и :АА называется отображение Г, определяемое как (Г)(х) = Г((х)).
Если Г=, то Г2(х)=Г(Г(х)), Г3(х)=Г(Г2(х)), … Гn(х)=Г(Гn-1(х)); Г0(х)=Г(Г-1(х))=(ГГ-1)(х)=x
Пример:
А – множество людей;
Г(А) – множество детей;
Г2(А) – множество внуков;
Г3(А) – множество правнуков;
Г-1(А) – множество родителей;
Г-2(А) – множество ???;
Слайд 43Функции
Однозначное отображение f:XY называется функцией. Однозначность означает, что для любых
пар (x1,y1)f и (x2,y2)f
из x1 = x2 следует y1
= y2.
Если YR, то функция f называется функцией с вещественными значениями.
Для любых пар (x,y)f y = f(x).
Формальное определение
f = { (x,y)XY | y = f(x) }
f – множество пар (x,y), определяющих соответствие
f(x) – обозначение элемента yY, соответствующего данному xX
Слайд 44Способы задания функций
Перечисление пар (х,у)
Формула преобразования х в у
График функции
Слайд 45Функции многих переменных
Если в выражении f:XY Х=UV,
то имеем функцию
2-х переменных f(u,v), где uU, vV.
Или формально
f = {
(u,v,y)UVY | y = f(u,v) }
Функция n переменных
f = { (x1,x2,…,xn,y)X1X2…XnY | y = f(x1,x2,…,xn) }
Слайд 46Операции над функциями
Обратная функция
f-1: Y X
Композиция функций
если
f: XY, g: YZ, то f g: XZ
z
= (f g)(x) = g(f(x))
Слайд 47Функционал
Функционал устанавливает зависимость между множеством чисел и некоторым множеством функций
(т.е. это зависимость числа от функции)
Например, определенный интеграл
число
функция
Слайд 48Оператор
Оператор устанавливает соответствие между двумя множествами функций, каждой функции одного
множества ставится в соответствие определенная функция другого множества.
Оператор дифференцирования
Слайд 49Отношения
Термин «отношение» обозначает некоторые виды соответствий, заданные на одном множестве.
Если
задано соответствие (Х,R),
то о элементе уR(х) говорят, что он
находится в отношении R к элементу х: у R х.
Отношением называется пара множеств (Х,R), где RХn.
Элементами множества Хn являются упорядоченные n-ки, и такое отношение называют n-арным или n-местным; множество упорядоченных пар элементов называют бинарным, упорядоченных троек - тернарным.
Слайд 50Отношения
Если R A2 - отношение, заданное на множестве А,
то
Обратное отношение R-1={(a,b) | (b,a)R}
Дополнение отношения R ={(a,b)
| (a,b)R}
Тождественное отношение I = {(a,a) | aA}
Универсальное отношение
U= {(a,b) | aA & bA} [U = A2]
Ядро отношения O = R° R-1
Слайд 51Свойства отношений
Рефлексивность
х R х - истинно ;
Антирефлексивность
х R х - ложно;
Симметричность
х R у
у R х ;
Антисимметричность
(х R у)&(у R х)
x=y ;
Несимметричность (полнота, или линейность)
Если (х R у) – истинно, то (у R х) – ложно;
Транзитивность
(х R у)&(у R z) x R z .
Слайд 52Теорема о свойствах отношений
Если RAA - отношение на
множестве А, то тогда
R - рефлексивно I R;
R -
антирефлексивно R I = ;
R - симметрично R = R-1;
R - антисимметрично R R-1 I;
R - несимметрично (полно) R I R-1 = U;
R - транзитивно R ° R R;
Слайд 53Замыкание отношений
Пусть R и R' - отношения на множестве А.
Отношение R' называется замыканием R относительно свойства С, если оно:
обладает
свойством C: C(R');
содержит отношение R: R R';
является наименьшим: C(R'') & RR'' R'R'' .
Примеры:
Транзитивное замыкание R - отношение
Рефлексивное транзитивное замыкание R -
( R0 = I, R1 = R, R2 = RR, …, Rn = Rn-1 R)
Слайд 54Отношение эквивалентности
Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и
транзитивно.
Элементы множества рассматриваются как эквивалентные тогда, когда любой из этих
элементов при некотором рассмотрении может быть заменен другим.
Например,
на множестве студентов – отношение «быть в одной группе» или «быть на одном курсе»;
на множестве целых чисел – «иметь одинаковый остаток при делении на число n».
Слайд 55Классы эквивалентности
Если на множестве Х определено отношение эквивалентности, то подмножество
элементов, эквивалентных некоторому элементу хХ, называют классом эквивалентности.
{Aj X |
j = 1n} – множество классов эквивалентности для множества Х.
Так как все элементы одного класса эквивалентности эквивалентны между собой, то всякий элемент хХ может находиться только в одном классе. Х будет являться объединением непересекающихся множеств Аj, так что полная система классов {Aj X | j = 1n} – есть разбиение множества Х.
Каждому отношению эквивалентности на множестве Х соответствует некоторое разбиение множества Х на классы эквивалентности Aj.
Слайд 56Отношения порядка
Отношения порядка определяют порядок расположения элементов множества.
Отношение является отношением
нестрого порядка, если оно рефлексивно, антисимметрично и транзитивно (, ,
, ).
Отношение является отношением строго порядка, если оно антирефлексивно, несимметрично и транзитивно (<,, >,,).
Множество Х называется упорядоченным, если сравнимы между собой любые 2 его элемента, то есть для них имеет место
x < y или x = y или x > y
Слайд 57Отношение доминирования
Между элементами множества Х имеет место отношение доминирования, если
эти элементы обладают следующими свойствами:
Антирефлексивность (никакой элемент не может доминировать
над самим собой).
Несимметричность (в каждой паре элементов только один из них может доминировать над другим).
Слайд 58Понятия высшей алгебры
Арифметические действия
(сложение, умножение, разность), введенные для вещественных
чисел, были распространены на другие объекты математики:
комплексные числа, вектора,
матрицы и пр.
Правила выполнения этих действий различны для разных объектов, но эти действия имеют общие свойства, на основе которых вводятся понятия
группы, кольца и поля.
Слайд 59Полугруппы
Говорят, что на множестве Х задана
алгебраическая операция , если
каждой упорядоченной паре (а, b)Х2 однозначным образом поставлен в соответствие
определенный элемент сХ этого множества Х, с = а b.
Алгебраическая операция ассоциативна, если для любых 3-х элементов а, b, и с множества Х выполняется соотношение (а b) с = а (b с).
Множество Х с заданной на нем ассоциативной операцией называется полугруппой.
Слайд 60Группы
Полугруппа называется группой, если
В множестве Х существует хотя бы 1
элемент е такой, что для любого элемента а данного множества
Х имеет место а е = е а = а
И для любого элемента а данного множества Х всегда найдется в этом множестве Х хотя бы 1 элемент а-1Х такой, что а а-1 = а-1 а = е
Если операция – умножение, то элемент е называется единицей группы, а элемент – а-1 обратным элементом а.
Если операция – сложение, то элемент е называется нулем группы ( 0 ), а элемент – а-1 противоположным элементом ( -а ).
Группа называется конечной, если Х – конечное множество.
Примеры: ({N, 0}, +); ({xN | mod2(x) = 0}, +);
({xR | x 0}, ×); ({1, -1, i, -i}, ×)
Слайд 61Кольца
Кольцом называется множество Х с определенными на нем 2-мя алгебраическими
операциями [сложением ( + ) и умножением ( * )],
причем
Операция сложения коммутативна
( а+b = b+а )
Операция умножения связана с операцией сложения дистрибутивным законом
a*(b + c) = a*b + a*c
(a+b)*c = a*c + b*c
Например, ({N,0},{+,*}); (R,{+,*}); ({R,i},{+,*}).
Слайд 62Поля
Кольцо, в котором для любого отличного от нуля элемента а
и любого элемента b существует ровно 1 элемент х такой,
что а*х = b, называется полем.
х = а / b – частное от деления а на b.
Например, полями являются кольца вещественных и комплексных чисел.