Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дистанционная подготовка к Всероссийской олимпиаде по информатике
Содержание
- 1. Дистанционная подготовка к Всероссийской олимпиаде по информатике
- 2. Занятие 2. Основы оценки сложности алгоритмов. Поиск НОД и НОК. Системы счисления
- 3. Знакомство с понятием сложности алгоритмаПри сравнении
- 4. Сложность алгоритма Сложность алгоритма – функция FA(n),
- 5. Важные определения
- 6. Важные определения
- 7.
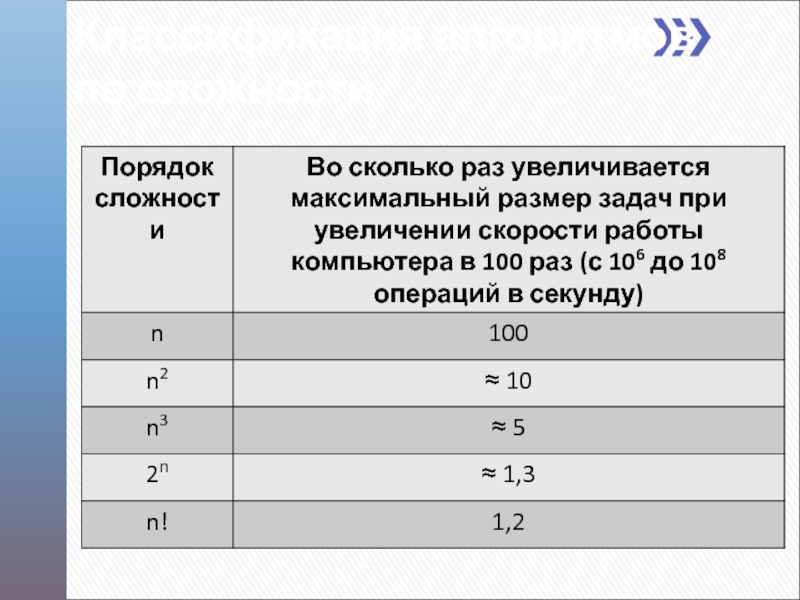
- 8. Характер возрастания сложности
- 9. Классификация алгоритмов по сложности
- 10. Примеры задач
- 11. Примеры задач
- 12. Бинарный алгоритм ЕвклидаБинарный алгоритм Евклида выполняется примерно
- 13. Поиск наименьшего общего кратного
- 14. b=a mod p -> остаток от деления
- 15. Система счисления – система записи чисел с
- 16. Базис ПСС – последовательность чисел, каждое из
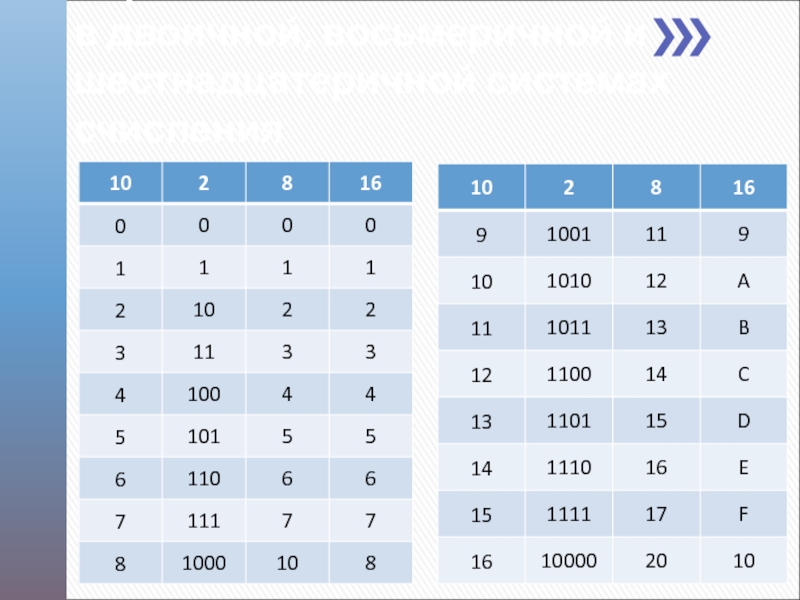
- 17. Первые числа в двоичной, восьмеричной и шестнадцатеричной системах счисления
- 18. Сложение Вычитание Умножение Деление(действуют обычные правила
- 19. an…a2a1a0 P = an*Pn + … +
- 20. Скачать презентанцию
Занятие 2. Основы оценки сложности алгоритмов. Поиск НОД и НОК. Системы счисления
Слайды и текст этой презентации
Слайд 1Дистанционная подготовка к Всероссийской олимпиаде по информатике
Преподаватель:
к.ф.-м.н., заведующий кафедрой ВТиКГ
ДВГУПС, преподаватель программы IT-школа Samsung,
Слайд 3Знакомство с понятием
сложности алгоритма
При сравнении производительности различных алгоритмов решения
задачи следует учитывать, что скорость выполнения компьютерных программ зависит от:
вычислительной производительности процессора ЭВМ,
объема кэш-памяти, оперативной памяти,
скорости доступа к запоминающим устройствам и т.п.
Поэтому время работы программы измеряется количеством операций
Главную роль играет характер возрастания числа элементарных операций при увеличении объема данных в задаче.
Кроме того, обычно учитывают объем памяти, которая используется во время работы программы
Эффективным решением олимпиадной задачи является такое, что:
укладывается в ограничения по времени работы программы
укладывается в ограничения ресурсов памяти, требующейся для выполнения программы
написано за кратчайшее время
Слайд 4Сложность алгоритма
Сложность алгоритма – функция FA(n), определенная как наибольшее
количество элементарных действий при решении задачи с объемом входных данных
n с помощью алгоритма АНапример:
на вход подается n чисел, следует вычислить их сумму
тогда сложность алгоритма определяется количеством операций сложения и линейно зависит от n
Слайд 12Бинарный алгоритм Евклида
Бинарный алгоритм Евклида выполняется примерно на 60% быстрее
традиционного.
Бинарный алгоритм Евклида основан на соотношениях (a>b):
Слайд 14b=a mod p -> остаток от деления a на p
равен b
Пример: 5 mod 3=8 mod 3=2
Свойства арифметических операций
(a+b) mod
p = ((a mod p) + (b mod p)) mod p(a-b) mod p = (p + (a mod p) – (b mod p)) mod p, при а>b
-a mod p= (p-a) mod p
(a*b) mod p = ((a mod p) * (b mod p)) mod p
Аналогичной формулы для деления нет! Поскольку обратный элемент по умножению существует только когда НОД (a, p)=1
Операцию деления можно выполнить только найдя обратный элемент по модулю p с помощью расширенного алгоритма
Арифметика остатков
Слайд 15Система счисления – система записи чисел с помощью определенного набора
цифр
Цифры – символы, с помощью которых записываются числа в системе
счисленияАлфавит – совокупность символов, используемых для записи чисел
Основание системы счисления – количество цифр, используемых для записи чисел
Позиционная система счисления – система счисления, в которой количественный эквивалент цифры зависит от ее положения в записи числа
5047 = 5*1000 + 0*100 + 4*10 + 7*1
Позиционные
системы счисления (ПСС)
Слайд 16Базис ПСС – последовательность чисел, каждое из которых задает «вес»
соответствующего разряда
Традиционная ПСС – система счисления, базис которой образуют члены
геометрической прогрессии, знаменатель P>1 – натуральное число,
значения цифр – целые числа
…, P-3, P-2, P-1, 1, P1, P2, P3, …
P – основание P-ричной системы счисления
Примеры нетрадиционных СС
Фибоначчиева система счисления
Алфавит: цифры 0 и 1
Базис: последовательность чисел Фибоначчи 1, 2, 3, 5, 8, 13, 21, 34, …
Факториальная система счисления
Алфавит: количество цифр увеличивается с ростом номера разряда
Базис: 1!, 2!, 3!, …
Позиционные
системы счисления (ПСС)
Слайд 18 Сложение
Вычитание
Умножение
Деление
(действуют обычные правила выполнения
операций «в столбик», подробнее рассмотрим в следующей лекции)
Арифметические
операции в
ПСС
Слайд 19an…a2a1a0 P = an*Pn + … + a2*P2 + a1*P1
+a0*P0
B0F916 = [1110][010][1510][910] =
= 1110*16103 + * 1510 16101
+ 910 *16100 = 4530510Схема Горнера:
Перевод целых чисел
из P-СС в 10-СС
![an…a2a1a0 P = an*Pn + … + a2*P2 + a1*P1 +a0*P0B0F916 = [1110][010][1510][910] = = 1110*16103 +](/img/thumbs/b23490b14155ef38d80f39bd0f7f19cd-800x.jpg "Дистанционная подготовка к Всероссийской олимпиаде по информатике an…a2a1a0 P = an*Pn + … + a2*P2 + a1*P1 +a0*P0B0F916")
