Слайд 2§1 Способи представлення графів
Графічне задання – відображення графа за допомогою
точок і ліній;
Матриця суміжності - ефективна для насичених графів;
Матриця інцидентності
– ефективний для розріджених графів;
Список суміжних вершин – ефективний для розріджених графів;
Список ребер – ефективний для розріджених графів.
Слайд 31.1 Матриця суміжності
Матрицею суміжності графа G , яка відповідає заданій
нумерації вершин, називають булеву квадратну матрицю А з елементами аij(i,j
=1,..., n,) де
Властивості:
Об'єм необхідної пам'яті О(|V2 |).
Швидке визначення присутності ребра (i,j) в графі.
За час О(1) отримуємо доступ до елементу аij матриці.
Для неорієнтованого графа матриця суміжності симетрична відносно головної діагоналі.
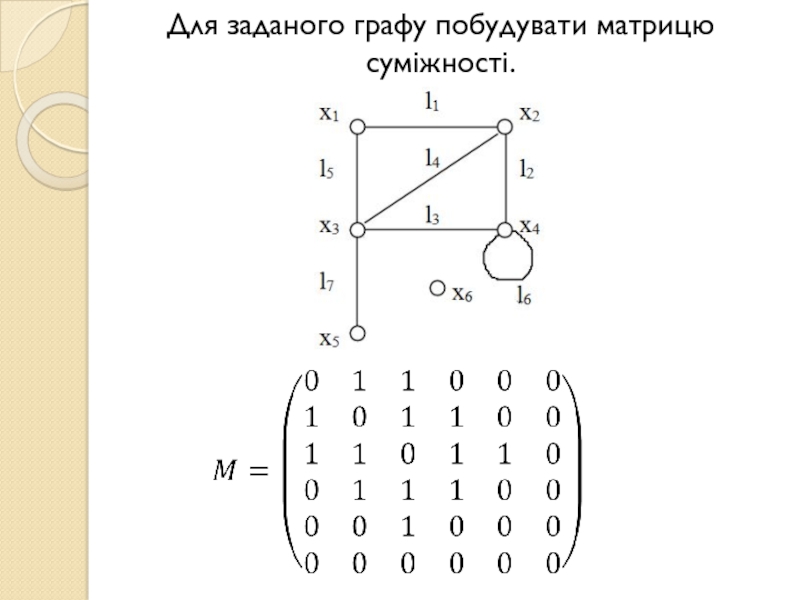
Слайд 4Для заданого графу побудувати матрицю суміжності.
Слайд 51.2 Матриця інцидентності
Матрицею інцидентності (або матрицею інциденцій) неорієнтованого графу G
називається матриця mn В = (bij), у якої
Слайд 61.3 Список суміжних вершин
Список суміжних вершин – це масив
A[n], кожен елемент A[i] якого містить список вузлів суміжних з
вершиною і.
A= {(1,2), (1,4), (2,1), (2,3), (2,5), (2,6), (3,2), (3,4), (3,6), (4,1), (4,3), (5,2), (6,2), (6,3), (6,6)}
Слайд 7Реалізація списку суміжних вершин на основі масивів A[n+1] та L[2m].
Слайд 81.4 Список ребер
Пара [u, v] відповідає ребру {u,v}, якщо граф
неорієнтований, і дузі (u,v), якщо граф орієнтований.
Об'єм пам'яті у
випадку представлення графа списком ребер дорівнює 2т (т - кількість ребер або дуг) - це найекономніший щодо пам'яті спосіб. Недолік - велика (порядку т) кількість кроків для знаходження множини вершин, до яких ідуть ребра або дуги із заданої вершин.
l1(x1,x2)
l2(x2,x4)
l3(x3,x4)
l4(x2,x3)
l5(x1,x3)
l6(x4,x4)
l7(x3,x5)
Слайд 9§2 Маршрути, ланцюги та цикли
Нехай G= (X, U) – скінченний
неорієнтований граф.
Скінчена послідовність вершин та ребер графа
x0 u1x1
u2 x2…xk−1uk xk, в якій кожне ребро uk є ребро, яке з’єднує вершини xk−1 та xk, називається маршрутом на графі G.
Маршрут з’єднує вершини x0 та xk.
Число k називають довжиною маршруту, тобто це кількість ребер, які входять до маршруту.
Маршрут називають замкненим, якщо x0 = xk.
Слайд 10Маршрут, в якому всі ребра є різні, називають ланцюгом.
Замкнений
ланцюг називають циклом.
Ланцюг називають простим, якщо всі його вершини є
різні.
Простий цикл – це цикл, у якому всі вершини, окрім першої та останньої, є різні.
Граф без циклів називається ациклічним, в іншому разі граф називається циклічним.
Кожна вершина з’єднується сама з собою маршрутом довжини 0 і цей маршрут є простим циклом. Такий цикл називають нульовим (якщо сказано просто цикл, то мається на увазі, що він не є нульовий).
Слайд 11Маршрут – x1 u1 x2 u1 x1 u4 x4 u3
x3 u3 x4 u5 x5
Ланцюг (всі ребра різні) – x1
u4 x4 u9 x2 u2 x3 u3 x4 u5 x5
Простий ланцюг (всі ребра і вершини різні) –
x1 u4 x4 u9 x2 u2 x3 u7 x5
Цикл – x1 u1 x2 u9 x4 u3 x3 u7 x5 u5 x4 u4 x1
Простий цикл – x1 u4 x4 u9 x2 u1 x1
Слайд 12§3 Орієнтовані графи
Поняття орієнтованого графа (орграфа) виникає, якщо ребрам графа
надати напрямок (тобто орієнтацію) в такий спосіб, що один з
кінців ребра буде початком, а інший – кінцем.
Стверджуватимемо, що задано орієнтований граф, якщо зазначено два об’єкти:
1) не порожня скінчена множина X – вершини графа;
2) множина U, утворена з упорядкованих пар вершин.
Елементи множини U називають дугами. Дуга орієнтованого графа зображується відрізком із зазначенням напрямку (стрілкою)
Слайд 13Орієнтований граф G = (X,U), де
X = {x1, x2, x3,
x4, x5};
U = {(x1, x2), (x1, x3), (x2, x3),
(x4, x1), (x4, x4)}.
Якщо u1=(x1, x2) – дуга орграфа, то стверджують, що дуга u1 виходить з вершини x1 і закінчується у вершині x2 .
Для орієнтованих графів замість степеня вершини х вводять поняття півстепенів: додатні d+(x) й від’ємні d-(x) півстепені вершини х:
d+(x) − число дуг, які входять до вершини x;
d-(x) − число дуг, які виходять з вершини x.
d+(x1)=1 d-(x1)=2
Слайд 14§4 Способи задання орієнтованих графів
4.1 Матриця суміжності
Матрицею суміжності орграфа G
називається квадратна матриця А(G) = [aij] порядку n, в якої:
Слайд 154.2 Матриця інцидентності
Матрицею інцидентності (або матрицею інциденцій) орграфа G називається
матриця
B(G) = [bij] порядку n×m, в якої елементи:
Слайд 16Матрицю суміжності можна визначити і для псевдографів. Тоді в разі
орієнтованого (неорієнтованого) псевдографа aij=k, де k – кратність дуги (xi,xj)
(ребра {xi,xj}) у цьому псевдографі.
x3
x1
x2
x4
x5
Слайд 17§5 Маршрути, шляхи та контури орієнтованого графа
Орієнтовані маршрути: в орграфі
рух за маршрутом допускається лише в напрямках, зазначених стрілками.
Маршрут, який
не містить повторних дуг, називається шляхом, а той, що не містить повторних вершин, – простим шляхом. Замкнений шлях називається контуром, а простий замкнений шлях – простим контуром.
Граф без циклів називається безконтурним, в іншому разі орграф називається контурним.
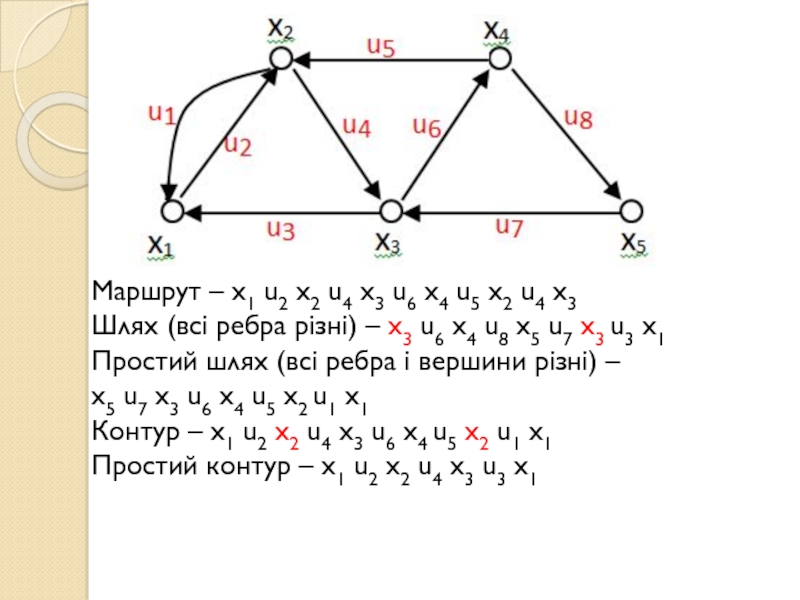
Слайд 18Маршрут – x1 u2 x2 u4 x3 u6 x4 u5
x2 u4 x3
Шлях (всі ребра різні) – x3 u6
x4 u8 x5 u7 x3 u3 x1
Простий шлях (всі ребра і вершини різні) –
x5 u7 x3 u6 x4 u5 x2 u1 x1
Контур – x1 u2 x2 u4 x3 u6 x4 u5 x2 u1 x1
Простий контур – x1 u2 x2 u4 x3 u3 x1




![Лекція 7. Графи 1.3 Список суміжних вершин Список суміжних вершин – це масив A[n], 1.3 Список суміжних вершин Список суміжних вершин – це масив A[n], кожен елемент A[i] якого містить список](/img/thumbs/42681ef561112b75a6548e767d8b44e8-800x.jpg)
![Лекція 7. Графи Реалізація списку суміжних вершин на основі масивів A[n+1] та L[2m]. Реалізація списку суміжних вершин на основі масивів A[n+1] та L[2m].](/img/thumbs/91adb34f4abf60ce68677a3ea861de6b-800x.jpg)
![Лекція 7. Графи 1.4 Список ребер Пара [u, v] відповідає ребру {u,v}, якщо граф неорієнтований, 1.4 Список ребер Пара [u, v] відповідає ребру {u,v}, якщо граф неорієнтований, і дузі (u,v), якщо граф орієнтований.](/img/thumbs/024bf4aa805f18a6a137bfdf465bc0a0-800x.jpg)





![Лекція 7. Графи §4 Способи задання орієнтованих графів4.1 Матриця суміжностіМатрицею суміжності орграфа G називається §4 Способи задання орієнтованих графів4.1 Матриця суміжностіМатрицею суміжності орграфа G називається квадратна матриця А(G) = [aij] порядку](/img/thumbs/1263ef5cd73c66c8e655abf6c429da5a-800x.jpg)
![Лекція 7. Графи 4.2 Матриця інцидентностіМатрицею інцидентності (або матрицею інциденцій) орграфа G називається матриця 4.2 Матриця інцидентностіМатрицею інцидентності (або матрицею інциденцій) орграфа G називається матриця B(G) = [bij] порядку n×m, в](/img/thumbs/deaeb3fd79314c3b116f577f27116a0a-800x.jpg)