Слайд 1Дисциплина “ИНФОРМАТИКА”
Специальность 036401.51 – «Таможенное дело»
ЛЕКЦИЯ 2
КОДИРОВАНИЕ ДАННЫХ
План
1. Понятие кодирования
2.
Кодирование данных двоичным кодом
3. Системы счисления
3.1. Позиционные системы счисления
3.2.
Перевод чисел в позиционных системах
3.3. Арифметические операции в позиционных системах
4. Кодирование текстовых, графических данных.
Кодирование звуковой информации.
Слайд 21. Понятие кодирования
Кодирование – преобразование данных одной формы представления (
из одной знаковой системы) в другую.
Примеры: человеческие языки (кодирование
языка с помощью графических символов), запись математических выражений, телеграфная азбука Морзе, код Бройля для слепых и др.
Каждая знаковая система строится на основе определенного алфавита и правил выполнения операций над знаками.
Для автоматизации работы на компьютере с данными, относящимися к разным типам (числа, тексты, звук, видео), очень важно унифицировать форму их представления. Для тоже используют кодирование.
Слайд 32. Кодирование данных двоичным кодом
В вычислительной технике существует своя система
кодирования – двоичное кодирование, основанное на представлении данных последовательностью всего
двух знаков 0 и 1.
Эти знаки называются двоичным кодом (англ. Binary digit) или бит.
Компьютер может обрабатывать числовые, текстовые, графические, звуковые и видео данные. Все эти виды данных кодируются в последовательности электрических импульсов: есть импульс (1), нет импульса (0).
Такие логические последовательности нулей и единиц называются машинным языком.
Слайд 4
1 битом можно выразить два понятия: 0 или 1 (да
иди нет, есть сигнал или нет сигнала, черное или белое,
истина или ложь и т.п.).
2 битами уже можно выразить четыре различных понятия (22) – 00 01 10 11.
3 битами можно закодировать уже восемь различных понятий (23) – 000 001 010 100 101 110 101 111.
Увеличивая на единицу количество разрядов в системе двоичного кодирования, можно увеличить в два раза количество значений, которое можно закодировать:
N=2n
n – число разрядов (бит),
N - количество значений.
Слайд 5
Увеличивая на единицу количество разрядов в системе двоичного кодирования, можно
увеличить в два раза количество значений, которое можно закодировать:
N=2n,
где
n – число разрядов (бит),
N - количество значений.
Компьютер может обрабатывать числовые, текстовые, графические, звуковые и видео данные. Все эти виды данных кодируются в последовательности электрических импульсов: есть импульс (1), нет импульса (0).
Такие логические последовательности нулей и единиц называются машинным языком.
Слайд 63. Системы счисления
Числа записываются с использованием особых знаковых систем, которые
называются системами счисления.
Системы счисления разделяются на два класса: позиционные и
непозиционные.
В непозиционных системах значение цифры не зависит от места, которое он занимает в числе.
Например, римская система счисления (состоит из 7 знаков): I(1) V(5) X(10) L(50) C(100) D(500) M(1000)
III – 3, LIX – 59, DLIV – 554.
В позиционных системах счисления значение цифры зависит от места, которое он занимает в числе.
Пример - десятичная система счисления:
25110
При работе с компьютерами приходится параллельно использовать несколько позиционных систем счисления – двоичную, восьмеричную, шестнадцатеричную.
Слайд 7
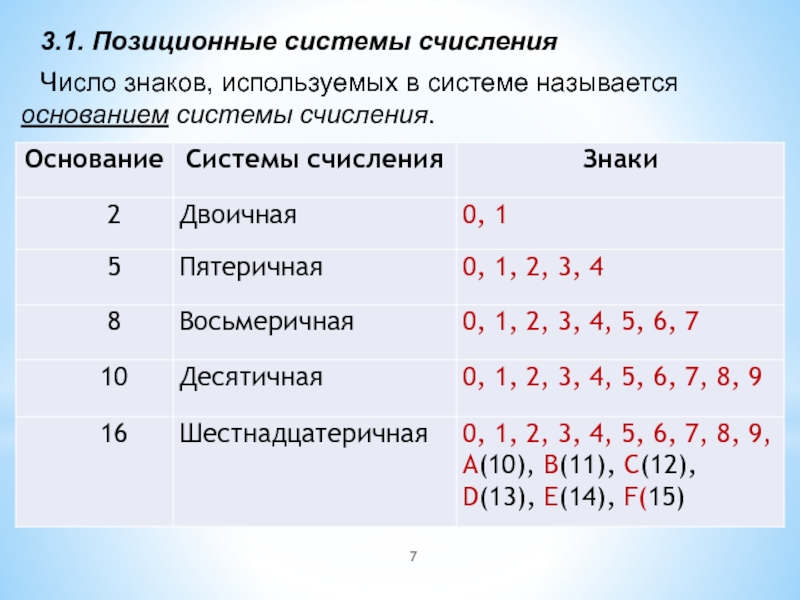
3.1. Позиционные системы счисления
Число знаков, используемых в системе называется
основанием системы счисления.
Слайд 83.2. Перевод чисел в позиционных системах
Перевод чисел в десятичную систем
счисления
В позиционных системах счисления число может быть представлено в
свернутом виде или в развернутом (как суммы произведений коэффициентов на степени основания системы счисления).
Если произвести арифметические действия в разверну-том представлении числа (в правой части равенства), то получится число в десятичной системе счисления.
Примеры.
23,4310 = 2*101 + 3*100 + 4*10-1 + 3*10-2
11012 = 1*23 + 1*22 + 0*21 + 1*20 = 1310
341,58 = 3*82 + 4*81 + 1*80 + 5*8-1 = 225,62510
A1F,416 = A*162 + 1*161 + F*160 + 4*16-1 = 2591,2510
.
Слайд 9 Перевод чисел из десятичной системы счисления в двоичную, восьмеричную,
шестнадцатеричную
Целая и дробная части переводятся порознь!
Для перевода целой
части числа необходимо ее разделить на основание системы счисления и продолжать делить частные от деления до тех пор, пока частное не станет меньше основания.
Значение получившихся остатков, взятые в обратной последовательности, образуют искомое число.
2510 2 2510= 110012
1 12 2 Проверяем:
0 6 2 110012 = 1*24+1*23+0*22+0*21+1*20=2510
0 3 2
1 1
Слайд 10Алгоритмы перевода дробей из десятичной системы счисления в двоичную
Нужно последовательно
выполнять умножение исходной десятичной дроби и получаемых дробных частей произведений
на основание системы до тех пор, пока не получится нулевая дробная часть или не будет достигнута требуемая точность вычислений. Затем взять целые части произведений.
0,7310
0,73 * 2 = 1,46 (целая часть 1)
0,46 * 2 = 0,92 (целая часть 0)
0,92 * 2 = 1,84 (целая часть 1) и т.д.
0,7310 = 0,1012
25,7510 2510= 110012
0,75 * 2 = 1,5
0,5 * 2 = 1,0 25,7510 = 11001,112
Слайд 11
Пример перевода числа из десятичной системы счисления в восьмеричную
192, 2410
Целая
часть Дробная
часть
19210 8 0,2410
0 24 8 0,24*8 = 1,92 (Целая часть 1)
0 3 0,92*8 = 7,36 (Целая часть 7)
0,36*8 = 2,88 (Целая часть 2)
Целая часть в восьмеричной: Дробная часть в восьмеричной:
3008 0,172..8
Результат:
192, 2610 = 300,172..8
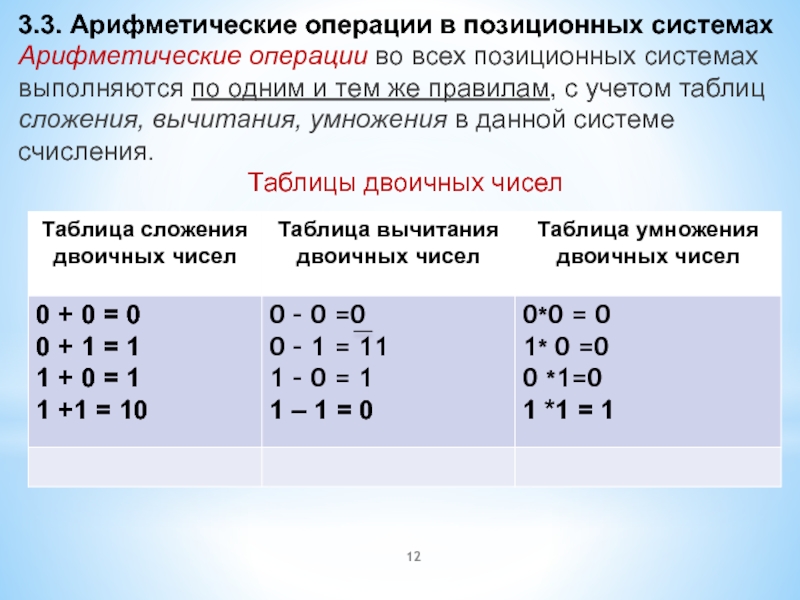
Слайд 123.3. Арифметические операции в позиционных системах
Арифметические операции во всех позиционных
системах выполняются по одним и тем же правилам, с учетом
таблиц сложения, вычитания, умножения в данной системе счисления.
Таблицы двоичных чисел
Слайд 131). При сложении, если происходит переполнение разряда (когда число становится
>= основания), производится перенос в старший разряд.
2). При вычитании, если
из меньшего числа (0) вычитается большее, (1) производится заем из старшего разряда (обозначено черточкой).
3). Умножение происходит в соответствии с таблицей по обыч-ной схеме, применяемой в десятичной системе счисления.
4). Деление выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.
Слайд 14Арифметические операции в восьмеричной и шестнадцатеричной системах счисления
Помнить! Величина переноса
в следующий разряд при сложении и заем из старшего разряда
при вычитании определяется величиной основания системы.
Слайд 154. Кодирование текстовых, графических данных. Кодирование звуковой информации
Если каждому символу
алфавита сопоставить определенное число, то с помощью двоичного кода можно
закодировать текстовую информацию. Восемь двоичных кодов (8 бит - 1 байт) достаточно для кодирования 256 различных символов (28=256).
Этого хватит, чтобы выразить различными комбинациями 8 битов все символы английского и русского языков, знаки препинаний, знаки арифметических действий и другие символы.
Слайд 16Для английского языка введена система кодирования ASCII (American Standard Code
for Information Interchange – стандартный код информационного обмена).
В этой
системе закреплены две таблицы кодирования – базовая и расширенная.
Базовая таблица закрепляет значения кодов от 0 до 127, а расширенная от 128 до 255.
Первые 32 кода закреплены за производителями компьютеров и программного обеспечения (для так называемых управляющих кодов).
С 32 кода по 127 - размещены коды символов английского языка, арифметических действий и др. символов.
Со 128 по 255 коды – используются для символов национальных языков.
Слайд 17В нашей стране существует несколько систем кодирования, которые вводятся в
расширенную таблицу ASCII (со 128 по 255 коды):
КОИ-7 (код обмена
информацией);
КОИ-8 (код обмена информацией);
Windows 1251 (создана компанией Microsoft)
ISO - международный стандарт (используется редко);
ГОСТ – альтернативная.
Сейчас происходит постепенный переход на универсальную систему кодирования, основанную на 16-разрядном кодировании (до 65535 различных символов – UNICODE).