Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисциплина Инженерная Геодезия КОНТРОЛЬНАЯ РАБОТА № 1
Содержание
- 1. Дисциплина Инженерная Геодезия КОНТРОЛЬНАЯ РАБОТА № 1
- 2. Задача № 1Вычисление исходных дирекционных углов линий
- 3. Ориентирование линийВ геодезии при ориентировании линий за
- 4. Дирекционный угол линии Связь прямого и обратного
- 5. РумбыРумб - острый угол, отсчитываемый по часовой
- 6. Условия задачи № 1Вычислить дирекционные углы линий
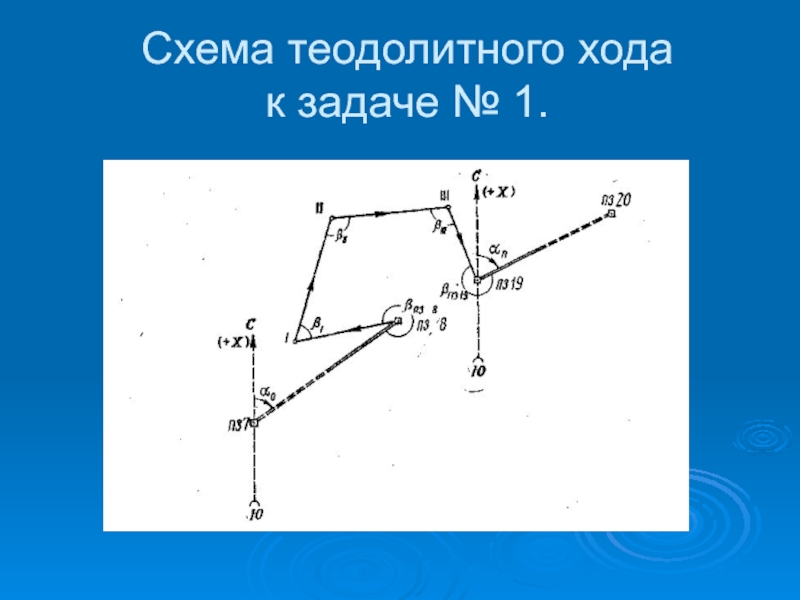
- 7. Схема теодолитного хода к задаче № 1.
- 8. Правило вычисления дирекционных угловдирекционный угол последующей стороны
- 9. РешениеαВС = 12 град.37,2мин. + 180 град.
- 10. Задача № 2Решение прямой геодезической задачи
- 11. Геодезическая задача – определение взаимного положения заданных
- 12. Прямая геодезическая задачаПриращения координат:ΔХ = ХВ –ХА
- 13. Знаки приращений ΔХ и ΔУ
- 14. Прямая геодезическая задачаВычислив приращения координат, можно найти
- 15. Условия и решение № 2Найти координаты Хс
- 16. Обратная геодезическая задачаПри известных координатах точек А(ХА;
- 17. Условие и решение задачи № 3Находим приращения
- 18. Скачать презентанцию
Задача № 1Вычисление исходных дирекционных углов линий
Слайды и текст этой презентации
Слайд 3Ориентирование линий
В геодезии при ориентировании линий за основное направление принимают
направление осевого, истинного или магнитного меридианов.
с помощью соответствующих углов ориентирования: дирекционного угла, истинного или магнитного азимута.Слайд 4Дирекционный угол линии
Связь прямого и обратного дирекционных углов:
αобр
= α ± 180°
Дирекционный угол –
это угол α
откладываемый по часовой стрелке от 0° до 360° между северным направлением координатной сетки карты (осевого меридиана) и направлением на объект. Принято различать прямое и обратное направление линии.
Прямой и обратный дирекционные углы отличаются друг от друга на 180 град.
Слайд 5Румбы
Румб - острый угол, отсчитываемый по часовой стрелке от ближайшего
направления осевого меридиана (вертикальные линии километровой сетки) до направления определяемой
линии.Прямой и обратный румбы в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей.
Связь между дирекционными углами и румбами:
СВ: r = α;
ЮВ: r = 180° - α, α = 180° - r;
ЮЗ: r = α - 180°, α = 180° + r;
СЗ: r = 360° - α, α = 360° - r.
Слайд 6Условия задачи № 1
Вычислить дирекционные углы линий ВС и СD,
если известны:
дирекционный угол αАВ линии АВ
измеренные правые по ходу
углы β1 = 189град.59.2 мин. и β2 = 168 град.50,8 мин.
Исходный дирекционный угол αАВ берётся в соответствии с шифром и фамилией студента:
число градусов равно двухзначному числу, состоящему из двух последних цифр зачётной книжки
число минут равно 30,2 мин. + столько минут, сколько букв в фамилии
Например: αАВ = 12 град. + 30,2 мин. + 7 мин. = 12 град.37,2 мин.
Слайд 8Правило вычисления дирекционных углов
дирекционный угол последующей стороны равен дирекционному углу
предыдущей стороны плюс 180 град. и минус горизонтальный угол по
ходу лежащий:αВС = αАВ + 180 град. – β1
αСD = αВС + 180 град. – β2
Слайд 9Решение
αВС = 12 град.37,2мин. + 180 град. –
- 189
град.59,2 мин. = 2 град.38 мин.
αСD = 2 град.38 мин.
+ 180 град. – - 168 град. 50,8 мин. = 13 град. 44,2 мин.
Слайд 11Геодезическая задача – определение взаимного положения заданных точек на поверхности
земли.
Прямая геодезическая задача.
По исходным координатам
точки А, горизонтальному
расстоянию от неё
до точки В и направлению
линии, соединяющей
эти точки (дирекционный
угол или румб)
определить координаты
точки В.
Слайд 12Прямая геодезическая задача
Приращения координат:
ΔХ = ХВ –ХА = SАВ*соsαАВ
ΔУ =
УВ – УА = SАВ*sinαАВ
Знаки приращений зависят
от знаков соs
αАВ и sinαАВСлайд 14Прямая геодезическая задача
Вычислив приращения координат, можно найти искомые координаты другой
точки:
ХВ = ХА + ΔХ
УВ = ХВ + ΔУ
Правило: координаты
каждой последующей точки равны координатам предыдущей точки плюс соответствующие приращения.Слайд 15Условия и решение № 2
Найти координаты Хс и Yс
Известны:
координаты
Хв = -14,02м; Yв = +627,98м
длина (горизонтальное проложение) линии ВС
- dвс = 239,14 мдирекционный угол αвс этой линии из задачи № 1 – αвс = 2 град.38 мин.
Вычисления
Хс = Хв + ΔХвс; ΔХвс = dвс * соs αвс
Ус = Ув + ΔУвс; ΔУвс = dвс * sin αвс
Слайд 16Обратная геодезическая задача
При известных координатах точек
А(ХА; УА) и В
(ХВ; УВ) найти
длину горизонтального проложения SАВ
направление линии АВ, т.е. дирекционный
угол αАВСлайд 17Условие и решение задачи № 3
Находим приращения координат:
ΔХ =
ХВ - ХА
ΔУ = УВ –УА
Вычисляем rАВ по tgrАВ =
ΔУ/ ΔХПо знакам приращений определяем четверть, в которой располагается румб и его название
Используя зависимость между дирекционными углами и румбами, находим αАВ
Вычисляем расстояние SАВ
SАВ = ΔХ /соs αАВ = ΔУ / sin αАВ
SАВ = √ ΔХ^2 + ΔУ^2